金融学原理 ch9 学习笔记 思维导图

普通股价值是指普通股预期能够提供的所有未来现金流量的现值。普通股价值评估既是对普通股未来流量现值的评估。

金融学原理 思维导图 ch9

• 金融学原理chapter9-- 普通股的价值评估
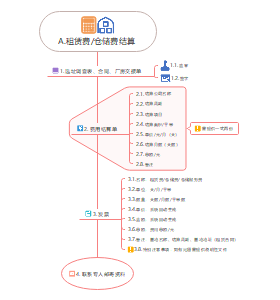
  • 解读股票行情表
    • 给出信息：
      • 提供了当前的实时价格，以及从上一交易日收盘开始的股票价格变动情况。
      • 开盘价和交易量也被给出。
      • 上一年的最高价与最低价也被给出
    • 红利收益率
      • 年度美元红利除以股票价格
        • 以百分比表示
    • 市盈率
      • 是股票价格于年度每股收益的比率
  • 两种估值方法
    • 折现红利模型DDM
      • 任何将股票价值作为预期未来红利现值进行计算的模型
        • 都是从普通股投资者预期收益由红利和价格差异构成的现象出发
        • 不含红利价格
          • 无权获得近期公告红利的股票价格
        • 排他性焦点在于红利
      • 预期收益率
        • E(r1)
      • 市场资本化比率（经过风险调整的折现率）
        • 是使投资者愿意投资该股票所要求的预期收益率
          • k
      • \latex E(r1) = k= \frac{D_1+P_1-P_0}{P_0}
        • 任意时期里的预期收益率均等于市场资本化比率k
      • 股票当前价格=
        • \latex P0= \frac{D_1+P_1}{1+k}
        • \latex P1 = \frac{D_2+P_2}{1+k}
          • 相当于现金流折现
        • \latex P0 = \frac{D_1}{1+k}+\frac{D_2}{(1+k)^2}...
      • 因此一只股票的价格是按照市场资本化比率进行折现的所有每股预期未来红利的现值
        • 若能估计红利，则能估计股价
      • 红利增长的情形：
        • 不变增长率，折现红利模型
          • 假设红利将以不变比率g增长
            • 则净利润、红利和股票价格都按相同不变增长率g增长
          • \latex P_0 = \frac{D_1}{k-g}=\frac{D_0(1+g)}{k-g}
            • 股票价格可望按照和红利相同比率增长
              • P1 = D2/(k-g) = (D1*(1+g))/(k-g)
              • P1 = (1+g)P0
                • 价格的预期变化率=g
            • [注意]：用红利模型计算得到的零时期股价不包含零时期的分红； 计算当期的股价，用下一期的红利。
            • 可以用红利增长模型估计必要回报率：
              • k = D1/p0 + g
          • 因此，该模型只有当预期红利增长率小于市场资本化比率k的时候才有效
            • k
        • 零增长
          • 每一期红利均相等
            • \latex P_0 = D/k
              • 相当于永续零增长年金
        • 不规则增长
          • 例题
            • 假设一家公司有望在第一年股息增加20％， 并在第二年股息增加15％。此后，股息将 无限期地以每年5％的速度增长。如果刚分 发的股息为1美元，必要的回报率为20％， 那么股票的价格是多少？
              • 计算股息，直到增长趋于平稳,.然后计算所有现金流的折现值
      • 思考：
        • 为什么现实中有些公司分红多股价却低？
          • 当前分红不代表未来分红预期，不是某一期红利决定股价，是未来所有红利
            • 比如公司业务高速增长时，不发分红
        • 依据上述模型，若要计算股票价格我们需要哪些已知变量？
          • 市场资本化比率
            • k
          • 红利的预期值
            • 但实际非常困难
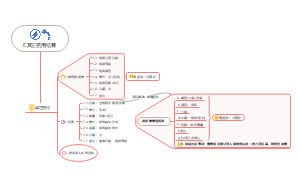
    • 盈利和投资机会
      • 折现现金流估值的另外一种途径是关注未来盈利与投资机会
        • 优势：
          • 有助于将分析师的注意力集中于价值的行业核心决定因素
        • 思考：
          • 在决定公司股价的问题上，利润与现金流哪一个更重要？
      • 公司的盈利分配：
        • 净利润=分红+留存收益
      • 假设不发行新股 （无其他外部融资）：
        • 公司新增投资资金来源=留存收益
        • 净利润 = 分红+新增投资
        • 红利_t = 盈利_t - 新投资净值
        • \latex P_0 = \sum^\inf_1 \frac{D_t}{(1+k)^t} =
          • \latex \sum^\inf_1 \frac{E_t}{(1+k)^t} - \sum^\inf_1\frac{I_t}{(1+k)^t}
            • E_t是盈利
            • I_t是净投资
              • 会影响E_t
            • 投资与公司盈利以及股票价格的关系
              • 投资净值>0，
                • 则Et会增加，因为净现值大于0，会增加净利润，所以会增加股价（前提是投资收益率大于要求的回报率）
        • 一家企业的价值不等于其预期未来收益的现值
          • 可能夸大或低估正确市场价值
            • 取决于净投资的正负
        • 该企业的价值等于预期未来盈利的现值减去再投资于企业的盈利的现值
          • 在一个扩张行业中，总投资规模可能超过更新所需的投资规模：
            • 净投资>0，而且生产能力随时间推移提高
          • 在一个衰退行业中，相反
      • 基于盈利和投资机会估计企业价值的原理：
        • 将企业价值分为两部分：
          • 作为永续年金投入未来的当前盈利水平的现值
          • 任何未来投资机会的净现值
        • P0 = E1 / k + 未来投资的净现值
          • E1由0时点的固定资产投资水平决定， 而且由于折旧投资，E1永久获得
            • 并不是通常意义上的每年盈利， 每年盈利还包括未来其他投资机会
        • 零增长公司
          • 将所有盈利都作为红利派发，也就是它的净投资为零
          • 这并不意味着该公司不投资，只是其投资等于折旧（也就是重置投资），因此净投资等于零
        • 当盈利不断增长 且每年将部分收入再投资于产生某收益率的新投资机会，
          • g = 盈利留存比例（即再投资比率）*新投资的预期收益率 = r*r1
            • r和r1的大小会决定股票现价是否大于盈利不增长时的股票现价
            • 假定全部留存用于投资
            • 等于预期红利增长率
              • 而不是实际派发出的红利的增长率
                • Dt=(1-r)Et
          • (远期）市盈率 =
            • \latex \frac{P_t}{E_{t+1}} = \frac{(1-r)E_{t+1}}{k-g} /{E(t+1)} = \frac{1-r}{k-g}
              • 是一个定值
                • 两个原因导致企业有更高市盈率：
                  • 低资本市场化比率
                  • 更好的未来投资机会
                    • 高成长
              • P0 = (1-r)E1/(k-g)
                • 注意：
                  • 当k=g
                    • 价值将趋于无穷大
                      • 但是这种情况在实际中不可能发生
                        • 因为增长率提高时， 企业风险增加， 投资者要求的收益率会增加
              • 注意：
                • 即使每股盈利、每股红利和股票价格可望每年按相同速度增长，这些增长对股价的总影响可能为0：
                  • 充分条件：r1 = k
                  • 即再投资利率等于市场资本化利率
          • （远期）红利收益率=
            • \latex \frac{D_{t+1}}{P_t} = \frac{D_t(1+g)}{D_t(1+g)/(k-g)} = k-g
        • 总结：
          • 增长本身不增加价值，增加价值的是投资机会
            • 当投资机会的收益率>k,才会被采纳，此时股价会变大
              • 这样的股票被称为：
                • 成长型股票
                  • g和k的较小变化都会导致市盈率的较大变化
            • 此外，当增大投资时，虽然g变大，但是D1会减小，难以实现股价提升（若g不够大）
            • 当投资机会的收益率=k，可以用P0 = E1/k估计该企业股票的价值
              • 再投资的净现值为0，并未增加股东股份的当前价值
    • 两种方法结果一样
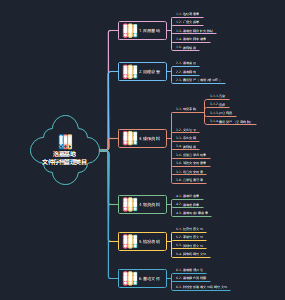
  • 鼓励政策是否影响股东财富？
    • 红利政策指的是在保持投资和借贷决策不变的条件下，向 投资者派发现金的企业政策
    • 股利政策：
      • 现金股利
      • 股票股利
      • 回购
    • 在不存在税收和交易成本的无摩擦金融环境里，
      • 无论股利政策如何，股东财富都相同
    • 现金红利和股票回购
      • 公司给股东发放现金的2种方法：
        • 支付现金股利
          • 所有股东都得到与其所拥有股份成比例的现金金额
          • 股票价格在支付完成后立即下降与红利相等的数量
            • 股东财富不受现金红利的影响
        • 回购股份
          • 只有选择出售部分股票的股东将得到现金
          • 股票价格保持不变
            • 出售股份者财富没有变化
            • 继续持有股份者财富也没有变化
      • 股票红利
        • 有时候公司进行股票拆分同时发放股票红利
          • 这些活动不向投资者派发现金
          • 增加股东的股份，但不改变其所有权的比例
          • 但是增加了流通股的数量
            • 比如： 2换1的股票拆分行动
              • 原来1股将被当成2股
              • 每股市场价格降至原来的1/2
                • 价格按比例降低（为保持总市场价不变）
              • 公司向每位股东派发额外股票
              • （相当于派发现金红利并要求其立即购买公司的额外股票， 没有派发现金，因此也无税收）
          • 还是不影响股东财富
    • 无摩擦环境中的红利政策
      • 莫迪利亚尼&米勒（MM）：
        • 在不存在税收和交易成本的无摩擦金融环境里，
          • 一家企业的股利政策可能对其股东财富没有任何影响
        • 本质：
          • 股东可以通过自身利益出发无成本地再投资红利或出售股票而战胜任何公司红利政策的影响
    • 真实世界里，摩擦包括：
      • 税收
        • 现金红利要缴纳个人所得税
          • 我国：
            • 红利税差别征收，
            • 资本利得免税
        • 股份回购可以避税，
      • 管制
        • 股份回购可以避税，但包括美国在内的很多国家限制此 类行为
        • 存在限制公司将运营不需要的现金留存在企业里的法律
      • 信息不对称（外源融资成本）
        • 现金红利和回购股票都会涉及从外部筹措资金的成本，
          • 提供中介服务的投资银行家必须得到回报
        • 内源性融资更能增加股东财富，因为外源性融资往往成本 过高
      • 红利反映的信号
        • 红利上升可能被解读为有利信号，导致股票上升
        • 红利下降可能被解读为不利的信号，导致股价下降
        • 因此公司管理层对变动红利支付尤为谨慎，并向公众做出解释