03价值评估基础

注会笔记-财务成本管理-价值评估基础，帮助考生梳理了考试的知识点，形成了清晰的知识体系。同时，通过对每个知识点的详细解释和关联，思维导图也促进了考生对知识的理解和记忆。因此，考生在备考过程中可以充分利用这张思维导图，提高备考效率，取得更好的成绩。

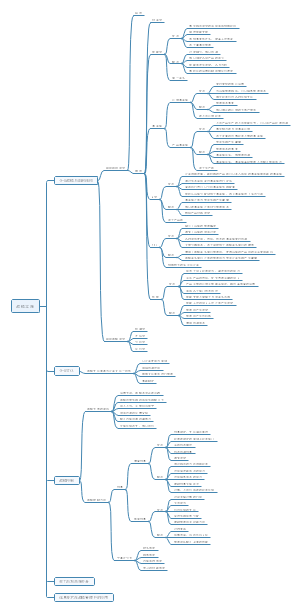
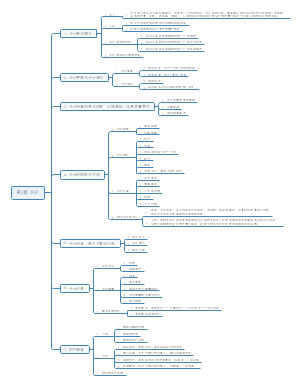
价值评估基础

• 利率
  • 利率概念
    • 一段时间内，利息与本金的比率
  • 基准利率
    • 含义
      • 金融市场上具有普遍参照作用的利率
      • 其他利率水平或金融资产价格均可根据这一基准利率水平来确定
    • 特征
      • 市场化
      • 基础性
      • 传递性
  • 公式
    • 利率r=纯粹利率r*+风险溢价RP
      • 纯粹利率r*
        • 无风险无通胀时，资金市场的平均利率。又称真实无风险利率
    • 风险溢价RP=IP+DRP+LRP+MRP
      • IP：通货膨胀溢价（Inflation　Premium）
      • DRP：违约风险溢价（Default　Risk　Premium）
      • LRP：流动性风险溢价（Liquidity　Risk　Premium）
      • MRP：期限风险溢价（Maturity　Risk　Premium）
        • 夜长梦多
    • （名义）无风险利率=r*+IP
  • 利率的期限结构
    • 客观题
    • 在任意时点，均可以用横坐标表示不同的到期期限，纵坐标表示到期收益率，从而画出两者之间的关系。画出的这条曲线就是“收益率曲线”，它展示了该时点的“利率的期限结构”，反映出长短期利率之间的关系。
    • 收益率曲线的种类
      • 上斜
      • 下斜
      • 水平
      • 峰型
    • 相关理论分类
      • 无偏预期理论
        • 影响利率期限结构的因素：完全取决于预期
        • 纯粹预期理论、预期理论
      • 市场分割理论
        • 影响利率期限结构的因素：预期和偏好选择等
      • 流动性溢价理论
        • 影响利率期限结构的因素：预期和市场流动性等
      • 有偏预期理论 先有一个预期，在预期的基础上调整
  • 报价利率和有效年利率
    • 复利的计息期间可以是年、季度、月、日
    • 报价利率
      • 又称名义利率
        • 以“年利率+每年复利次数（或计息期的天数）”为利息报价的方式
    • 计息期利率
      • 指给定“计息期间”的利率
      • 计息期利率=报价利率/每年复利次数
    • 有效年利率
      • 将计息期利率折算成每年复利一次的年利率，又称等价年利率
      • 假设每年复利次数为m, 有效年利率=（1+报价利率/m）^m-1
  • 连续复利
    • 当报价利率的计息期间越来越短、复利次数m越来越大，趋向正无穷大时，得到的利率叫做连续复利
    • 连续复利的有效年利率i=e^报价利率-1
• 货币时间价值
  • 凡是计算货币时间价值的题，都要先画时间轴
  • 基本概念
    • 货币时间价值，是指货币经历一定时间的投资和再投资所增加的价值
    • 提示1
      • 货币的时间价值通常用相对数表示，即纯粹利率
    • 提示2
      • 因为存在利息，所以在不同时间点，单位货币的价值不相等
  • 终值和现值
    • 终值
      • 又称将来值，是现在一定量资金在未来某一时点上的价值，俗称本利和，通常记作F
    • 现值
      • 又称本金，是指未来某一时点上的一定量资金折合到现在的价值，通常记作P
    • 计息期的划分
      • 计息期一般为1年
      • 注意需要把报价年利率转换为计息期利率
        • 假设报价年利率12%
        • 计息期1年
          • 计息期利率12%
        • 计息期半年
          • 计息期利率12%/2=6%
  • 复利终值和现值
    • 复利终值
      • 现在的一笔资金，按复利计算在将来某一时间的本利和
      • F=P×(1+i)^n=P×（F/P,i,n）
    • 复利现值
      • 指未来某一时点的特定资金按复利计算方法，折算到现在的价值，或者说是为取得将来一定本利和，现在所需要的本金
      • P=F·（1+i）^(-n)=F×（P/F,i,n）
  • 年金
    • 定义
      • 等额、定期的一系列现金流叫做年金
    • 普通年金
      • 普通年金终值
        • F=A×(F/A,i,n)
          • F=A*((1+i)^n-1)/i
        • 普通年金终值系数和偿债基金系数互为倒数
      • 普通年金现值
        • 是指将来收付的一组等额、定期（每期期末）的现金流，等效成现在就收付的款项金额，也是这组现金流的复利现值之和
        • P=A×(P/A,i,n)
          • A*((1-1/(1+i)^n)/i)
      • 年金现值系数是“本金”，年金终值系数是“本利和”
        • 即：(P/A,i,n)×(1+i^n=(F/A,i,n)，或 (P/A,i,n)×(F/P,i,n)=(F/A,i,n)
      • 项目 终值 现值 单利 F=P×(1+i×n) P=F/(1+i×n) 复利 F=P×(F/P,i,n) P=F×(P/F,i,n) 普通年金 F=A×(F/A,i,n) P=A×(P/A,i,n) 偿债基金 A=F/(F/A,i,n) 投资回收额 A=P/(P/A,i,n)
    • 预付年金
      • n期预付年金的终值系数=(n+1)期普通年金的终值系数-1
        • 记忆方法：年终假期（加期）
      • n期预付年金的终值系数=n期普通年金的终值系数×(1+i)
      • n期预付年金的现值系数=(n-1)期普通年金的现值系数+1
      • n期预付年金的现值系数=n期普通年金的现值系数×(1+i)
    • 递延年金
    • 永续年金
      • 永续年金没有终值
      • 现值P=A/i
    • 总结
      • 复利终值系数×复利现值系数=1
      • 年金终值系数=年金现值系数×复利终值系数
      • 各种年金之间的判断，关键是画出时间轴，定位现金流，逐个现金流分析向前/向后复利的次数。
• 风险与报酬
  • 难点
    • 难点一
      • 公式繁杂
      • 应对策略
        • 只记一个方差公式，其余利用“名称记忆法”掌握
    • 难点二
      • 习惯从坐标中获取风险与收益的信息，掌握“向上、向左、向左上”的思想
  • 风险的含义
    • 预期结果的不确定性
    • 风险即不确定性，用离散程度表示，可用方差、标准差、变异系数来计量离散程度
  • 风险如何计量
    • 概率已知
      • 期望报酬率
      • 方差σ2
        • 先求差，再平方，再乘以概率
      • 标准差σ
        • 方差开根号
    • 概率未知
      • 期望报酬率
      • 总体方差/样本方差
        • 先求差，再平方，除以样本数
      • 标准差σ
    • 变异系数
      • 标准差σ/预期值
      • 理性人应选择变异系数（=标准差/预期值）小的方案
  • 单项投资的风险与报酬公式
    • 预期值
      • 对报酬率求平均(用概率加权)，又称期望报酬率
    • 方差
    • 标准差
    • 1. 用离散程度（报酬率的各种可能性偏离预期值的程度）衡量全部风险 2.是绝对数，只有预期值一致才能比较风险高低，方差、标准差越大风险越高
    • 变异系数
      • 用相对数衡量全部风险
      • 变异系数越大，风险越大
  • 多项投资（即投资组合）的公式
    • 期望报酬率和风险
      • 假设投资组合中共有m种证券，Aj是第j种证券的投资占比，rj是第j种证券的期望报酬率，组合收益是各证券收益的加权平均
      • 投资组合理论
        • 组合收益是各证券收益的加权平均
    • 协方差
      • • 两只证券相同时，协方差变为方差
      • 差（报酬率-期望报酬率）的乘积再加总
    • 相关系数
      • 提示：不直接记忆复杂的相关系数公式，记忆最基础的方差公式，标准差、协方差、相关系数的公式从方差公式开始变换。这是教材第一个需要记忆的公式，参见下表“名称记忆法”
      • • 方差
          • 分子：差(报酬率-期望报酬率)的平方，再加总 分母：总体取N，样本取N-1
        • 协方差
          • 分子：差(报酬率-期望报酬率)相乘，再加总 分母：总体取N，样本取N-1
        • 标准差
          • 方差开根号
        • 相关系数
          • 协方差除以“方差”(即两个标准差相乘)，得到“协”，即相关性
      • 特征
        • r总是在-1~+1间取值，正负与协方差的正负相同。r=±1时的公式可由（*）推出
        • • 选择题常考
  • 用坐标轴画出风险与报酬
    • 只投资于一只证券
      • 1.用证券在不同情况下收益率（回报率）的平均值，即期望报酬率来衡量该证券的“报酬”水平
      • 2.用证券在不同情况下收益率（回报率）的离散程度，即该证券收益率的标准差来衡量该证券的“风险”程度
      • 用纵坐标表示期望报酬率，用横坐标表示标准差
        • 单只证券的风险与报酬是坐标轴图像中的一个点
    • 投资于两只证券的投资组合
      • 相关系数会影响投资组合的标准差
      • 当相关系数=1时，一半组合资金投资于证券A，另一半投资于证券B，将该投资组合的期望报酬率、标准差画在坐标轴上恰是AB连线的中点
      • 当相关系数<1时，一半组合资金投资于证券A，另一半投资于证券B，将该投资组合的期望报酬率、标准差画在坐标轴上将位于AB连线中点的正左侧
        • 期望报酬率与相关系数=1时相同， 所以是正左侧，有风险分散效应
      • 向左平移的越多，风险分散效应越大，直至相关系数r=-1
  • 投资组合的有效集
    • 投资于两只证券
      • 如果相关系数=1，则部分资金（Q）投资于证券A，剩余资金（1-Q）投资于证券B的投资组件，随着Q取值的变化（介于0、1之间），投资组合的期望报酬率和标准差构成连接AB的一条直线
      • 如果两者的相关系数小于1且固定，则部分资金（Q）投资于证券A， 剩余部分资金（1-Q）投资于证券B的投资组合，随着Q取值的变化 （介于0、1之间），投资组合的期望报酬率和标准差构成连接AB的 一条曲线。这条曲线叫做投资于证券A和B的投资组合的机会集
        • 机会集和有效集
          • 曲线1~6叫做“机会集”
        • 理性人的选择
          • 水平向左，即相同收益（水平）风险更低（向左）； 垂直向上，即相同风险（垂直）收益更高（向上）。
        • 几个关键之处
          • 曲线1~6最左端的点标准差最小，这个点对应的投资组合叫做“最小方差组合”。 “最小方差组合”点以下的曲线叫做“无效集”。因为可以垂直向上，找到曲线上拥有相同标准差，但期望报酬率更高的另一个点。 “最小方差组合”点以上的曲线叫做“有效集”，有效集对投资者而言风险收益比更佳。
        • 相关系数对机会集的影响
        • 相关系数为1，机会集是直线；相关系数小于1，机会集开始弯曲，相关系数越小，机会集曲线越弯曲，表明风险分散程度越高（即标准差小于加权平均值越多，即从AB连线上的点水平向左移动越多）。只有相关系数足够小，才会出现“无效集”。这是用图形展示了前序“相关系数r的特征”处列示的表格
    • 投资于多只证券
      • 机会集是一个平面（下图阴影部分）
      • 不在“曲线SR”上的任意一点A，可以垂直向上，找到曲线SR上拥有相同标准差但期望报酬率更高的点B；或者水平向左，找到曲线SR上拥有相同期望报酬率但标准差更低的点C；或者向左上方，找到曲线SR上拥有更高期望报酬率且标准差更低的点D。因此，对投资者而言，风险收益比更佳的有效集或有效边界SR位于机会集顶部，从最小方差组合点S到最高期望报酬率点R。有效集上的每一点，都是一种投资于各种证券的投资组合。由于证券属于风险资产，因此有效集是“风险组合”的有效集
  • 资本市场线
    • 思考：如果只能投资于风险资产，那么有效集是曲线SR（从最小方差组合点S到最高期望报酬率点R）；如果在投资于风险资产的同时，也可以投资无风险资产（例如国债），那么有效集将会发生什么变化？
    • 假设
      • 对无风险资产的使用没有限制，可以借入或贷出，报酬率都是Rf，标准差为0；投资于风险资产的组合，期望报酬率为rp，标准差为σp
    • 计算总期望报酬率和总风险
      • 对于包含无风险资产和风险资产组合的新投资组合，投资于风险资产组合P的资金占比为Q，投资于无风险资产的资金占比为1-Q，套用组合包含两只证券的相关公式，解得
      • 总期望报酬率=
      • 总标准差=
      • 【注】无风险资产收益率的标准差为0，即没有风险
    • 从无风险报酬率点Rf，做有效边界的切线，切点为M，则直线RfM是资本市场线。资本市场线位置由截距、切点决定
      • 直线RfM优于原有效边界（曲线SMN），是资本市场上投资者的最佳选择，所以叫做“资本市场线”
      • 切点M
        • 相较于有效边界上其他点，切点M是最有效的证券组合(风险资产组合)，叫做“市场组合”
      • 资本市场线的斜率=(Rm-Rf)/σm,反映出市场对风险的定价，即如何权衡风险与期望报酬率 斜率越大（越陡峭）越厌恶风险，风险补偿（Rm）越大
      • 风险偏好
        • 切点M是现时条件下，市场的最佳选择，即市场整体自发的均衡点，与个人的效用偏好（或风险偏好）无关
        • 如何在资本市场线上选择具体的点，反映出投资者个人的风险偏好。每个点代表不同的Q，即投资于风险资产组合的比重，剩余1-Q部分资金投资于无风险资产。Q越小，越厌恶风险；Q越大，越偏好风险。
  • 系统风险与非系统风险
    • 一项资产的必要报酬率高低取决于该资产的系统风险大小
    • 系统风险
      • 影响整个资本市场的风险，也称市场风险
      • 没有有效的方法消除
        • 不可分散风险
    • 整体风险用标准差计量
  • 资本资产定价模型
    • 系统风险的度量
    • 研究对象
      • 充分组合情况下风险与必要报酬率之间的均衡关系
    • 公式
      • 贝塔系数β=
      • 第i种证券与市场组合M报酬率之间的协方差用cov(Ki,Km)或σim表示
    • β值的含义
      • 贝塔系数反映出某资产的系统风险与市场组合的系统风险的关系
    • 投资组合的贝塔系数
    • 证券市场线
      • 资本资产定价模型CAPM
        • 公式
          • Ri=Rf+β*(Rm-Rf)
        • 参数Ri是第i只股票的必要报酬率，Rf是无风险报酬率，Rm是市场组合的必要报酬率，Rm-Rf是风险的价格，又称风险溢价率或风险补偿率
        • 投资者承担了系统风险β，就会要求风险补偿，承担的系统风险β越高，要求的风险补偿就会越高
      • 证券市场线
        • 位置由截距、斜率确定
        • 将上述公式在横坐标为贝塔系数、纵坐标为必要报酬率的直角坐标系中画出，就是证券市场线SML
        • 投资者的必要报酬率取决于：承担的市场风险β、无风险报酬率（截距）、市场的风险补偿程度（斜率-）
      • 比较两条线
  • 提示
    • 必要报酬率
      • 最低要求报酬率
      • 使用CAPM计算出来的
      • 准确反映预期未来现金流量风险的报酬率
        • 等风险投资的机会成本
    • 期望报酬率
      • 使净现值为0的报酬率
    • 两者之间的关系
      • 期望报酬率>必要报酬率
        • 投资有超额回报
      • 期望报酬率=必要报酬率
        • 理想状态下的资本市场，资产价格合理，投资获得与所承担风险相应的回报
      • 期望报酬率<必要报酬率
        • 无法获得应有回报
• 债券、股票价值评估
  • 债券价值评估
    • 债券是按约定时间支付利息（面值×票面利率），并在到期日偿还面值（本金）的有价证券
    • 债券价值的评估方法
      • Vd是债券价值，It是第t期利息，M是面值(即本金)，rd是折现率(等风险投资市场利率)，n是债券的剩余期数
    • 五种具体模型
      • 原理：利息符合等额、定期的特征，因此可以使用年金现值公式，面值本金部分可以通过复利现值公式计算，债券价值就是加总未来支付的利息和面值本金的现值
      • 基本债券
        • 按年付息
      • 平息债券
        • 一年付息C次
      • 零息债券
        • 不付息，又称纯贴息债券
      • 单利债券
        • 到期一次还本付息，单利计息
      • 流通债券
        • 距下次付息还有m年（m<1）
    • 债券价值的影响因素
      • 客观题
      • 面值、票面利率、折现率对债券价值的影响
      • 面值M
        • 面值越大，债券价值越大
      • 票面利率i
        • 票面利率越大，债券价值越大
        • 当票面利率大于/等于/小于折现率时，债券价值大于/等于/小于面值，因而分别叫做溢价/平价/折价债券
      • 折现率r
        • 折现率越大，债券价值越小
        • 计息期利率
          • 报价利率除以年内付息次数
        • 计息期折现率
          • 年折现率为有效年折现率，应计算出计息期折现率
      • 报价年折现率不变时，付息频率、到期时间对债券的影响
        • 付息频率加快、到期时间变长，都会加剧溢价或折价的趋势
        • 到期时间缩短，债券价值向面值回归：连续付息债券是连续回归，分期付息债券是周期波动回归面值
      • 有效年折现率不变时，付息频率加快债券价值上升
    • 债券的期望报酬率
      • 一般用到期收益率来衡量
      • 是指投资者以特定价格买入债券并持有至到期所获得的报酬率
      • 用该折现率计算投资者获得现金流量（利息、本金）的现值恰好等于债券买入价格
  • 普通股价值评估
    • 普通股价值的评估方法
      • 评估普通股价值通常使用现金流量折现模型和相对价值评估模型
      • 原理
        • 投资者购入股票是为了获取未来的现金流量（股利、卖出时的股价），股票为投资者带来的未来现金流量的现值就是股票的价值
      • 公式
      • 股票价格P0=D1/（rs-g），所以rs=D1/P0+g
      • 现在（0时点）以P0买入股票，一年后（1时点）获得股利D1，D1/P0恰好是股利收益率
      • g股利增长率
        • 在有效市场，股价的增速与股利的增速一致，因此g是股价增长率或资本利得收益率
  • 混合筹资工具价值评估
    • 既有债务性质又有权益性质的筹资工具叫做混合筹资工具，例如优先股、永续债、附认股权证债券、可转换债券等
    • 优先股的特殊性
      • 与普通股相比
      • 优先分配利润
        • 在完全支付约定的股息之前，不得向普通股股东分配利润
      • 优先分配剩余财产
      • 表决权限制
        • 除以下情况外，优先股股东不出席股东大会会议，所持股份没有表决权： （1）修改公司章程中与优先股相关的内容 （2）一次或累计减少公司注册资本超过10% （3）公司合并、分立、解散或变更公司形式 （4）发行优先股 （5）公司章程规定的其他情形
    • 价值评估方法和期望报酬率
      • 当市场有效时，价值 = 价格，期望报酬率 = 必要报酬率