第25章：抽样调查

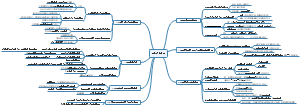
经济师经济基础知识第25章抽样调查的思维导图，从抽样调查基本概念、几种基本概率抽样方法、估计量和样本量这三个方面作了一个概述，方便大家学习记忆。

第25章 抽样调查

• 一、抽样调查基本概念
  • （一）抽样调查基本概念
    • 1.抽样调查的概念：是使用频率最高的一种调查方式。是指按照某种原则和程序，从总体中抽取部分单位，通过对这一部分单位进行调查得到信息，以达到对总体情况的了解，或者对总体的有关参数进行估计。
    • 2.几个基本概念 总体：调查对象的全体 总体单元或单位：组成总体的各个个体 样本（总体一部分）：由总体中按一定原则或程序抽出的部分个体所组成 入样单位：每个被抽中进入样本的单位 样本量：样本中包含的入样单位的个数
    • 3、总体参数与样本统计量 (1)总体参数一一变量的数字特征 1)是根据总体中所有单位的数值计算的。 2)常用的总体参数：总体总量，总体均值，总体比例，总体方差等。如，公司所有注册在职人员的平均工资。 (2)样本统计量（估计量）对总体参数的估计 1)是根据样本中各单位的数值计算的，是对总体参数的估计也称为估计量。 2)常用的样本统计量：样本均值、样本比例、样本方差等。如：用样本中员工的平均工资来估计该公司所有注册在职人员的平均工资。
    • 4、抽样框 (1)含义：供抽样所用的所有抽样单元的名单，是抽样总体的具体表现。 (2)抽样框形式：名录框(企业名录、电话簿、人员名册)也可以是一张地图或其他适当形式。 (3)案例：公司1000名注册在职人员的人员名册。 (4)但不管什么形式，抽样框中的单位必须是有序的，便于编号。
  • （二）概率抽样与非概率抽样
    • 1.概率抽样 (1)含义：也称随机抽样，是指依据随机原则，按照某种事先设计的程序，从总体中抽取部分单元的方法。 (2)分类：等概率抽样（每个单位被抽入样本的概率相等）和不等概率抽样（每个单位被抽入样本的概率不同） (3)特点 ①按一定的概率以随机原则抽取样本； ②总体中每个单元被抽中的概率是已知的，或者是可以计算出来的； ③当采用样本对总体参数进行估计时，要考虑到每个样本单位被抽中的概率。
    • 2.非概率抽样 (1)定义:又称为非随机抽样,是调查者根据自己的方便或主观判断抽取样本的方法，其最主要的特征是抽取样本时并不是依据随机原则。 (2)主要方法 判断抽样:指在抽取样本时，调查人员依据调查目的和对调查对象情况的了解，人为确定样本单元:“平均型单元” 方便抽样:指在抽取样本时，依据方便原则，以达到最大限度降低调查成本的目的:拦截式抽样 自愿样本:不是经过抽取，而是自愿接受调查的单元所组成的样本：网上调查比较典型 配额样本:指将总体中的各单元按一定标准划分为若干类型，将样本数额分配到各类型中，从各类型中抽取样本的方法则没有严格限制，一般采用方便抽样的方法抽取样本单元
  • （三）抽样调查的一般步骤
    • 1、确定调查问题一为什么要做、要做什么样的调查。
    • 2、调查方案设计一明确如何实施调查，设计抽样方案和问卷。
    • 3、实施调查过程一获得样本单元的数据，关键保证原始数据的质量。
    • 4、数据处理分析一检查、核对原始数据；合格数据编码、录入；数据预处理；数据分析；总体参数估计。
    • 5、撰写调查报告一最终成果，是前面劳动成果的展现
  • （四）抽样调查中的误差
    • 1.定义：样本估计值和总体参数真值之间的差异称为误差。
    • 2.种类
      • 抽样误差：是由于抽样的随机性造成的，用样本统计量估计总体参数时出现的误差。抽到哪一个样本完全是随机的，而抽到不同的样本，对总体的估计就会不同，这就是抽样误差产生的根本原因。 是指除抽样误差以外，由其他原因引起的样本统计量与总体真值之间的差异。
      • 非抽样误差：是指除抽样误差以外，由其他原因引起的样本统计量与总体真值之间的差异。 产生的原因： 抽样框误差：如把营业执照作为个体商业的抽样框，有些无照经营；有些虽有照但已转行；还有些一人多照。 无回答误差：随机因素：被调查者不在家或有病无法接受调查。非随机因素：被调查者不愿告诉实情拒绝回答。 计量误差：可能是由调查人员、问卷设计、受访者等原因造成的调查者诱导被调查者，调查中的提问错误或记录【答案】错误，调查人员有意作弊；由于问卷的原因受访者对调查问题的理解上有偏误；受访者记忆不清，受访者提供虚假数字等。
• 二、几种基本概率抽样方法
  • （一）简单随机抽样
    • 1.分类 不放回简单随机抽样：不放回简单随机抽样，即从包含N个单元的总体中逐个随机地抽取单元并无放回，每次都在所有尚未被抽入样本的单元中等概率的抽取下一单元，直到抽取n个单元为止。 有放回简单随机抽样：有放回的简单随机抽样是指从总体中随机抽出一个样本单元，记录观测结果后，将其放回到总体中去，再抽取第二个，如些类推，直到抽满n个单位为止。 总结：不放回简单随机抽样比放回抽样有更低的抽样误差
    • 2.优点：最基本的随机抽样方法，操作简单，且每个单位的入样概率相同，因而样本估计量形式也比较简单。
    • 3.缺点 (1)没有利用抽样框中更多的辅助信息，所以用样本统计量估计总体参数的效率受到影响； (2)在简单随机抽样条件下，样本的分布可能十分分散，增加了调查过程中的费用和时间。
    • 4.适用条件 (1)抽样框中没有更多可以利用的辅助信息。 (2)调查对象分布的范围不广阔。 (3)个体之间的差异不是很大。
  • （二）分层抽样
    • 1.概述：指先按照某种规则把总体分为不同的层，然后在不同的层内独立、随机地抽取祥本，这样所得到的样本称为分层样本。 如果每层中的抽样都是简单随机抽样，则称为分层随机抽样。
    • 2.特点 (1)分层抽样不仅可以估计总体参数，同时也可以估计各层的参数。 (2)便于抽样工作的组织。 (3)每层都要抽取一定的样本单位，这样，样本在总体中分布比较均匀，可以降低抽样误差。
    • 3.种类：等比例分配和不等比例分配。
    • 4.应用条件 抽样框中有足够的辅助信息，能够将总体单位按某种标准划分到各层之中，实现在同一层内，各单位之间的差异尽可能地小，不同层之间各单位的差异尽可能地大。
  • （三）系统抽样
    • 1.概念：指先将总体中的所有单位按一定顺序排列，在规定范围内随机抽取一个初始单元，然后按事先规定的规则抽取其他样本单元。最简单的系统抽样是等距抽样。
    • 2.优点 (1)操作简便，只需要随机确定起始单位，整个样本就自然确定了。 (2)对抽样框的要求也比较简单，只要求总体单位按一定顺序排列，而不ー定是一份具体的名录清单。例如，欲对某城市汽车尾气排放情况进行调查，抽样比为1%,即平均每100辆车中抽1辆，采用系统抽样，可以将汽车牌号作为一种排列，在1-100中随机抽取个号，如53,结果凡牌号尾数为53的车辆均作为样本单位。
    • 3.缺点：方差估计比较复杂，给计算抽样误差带来一定困难。
    • 4.系统抽样的估计效果与总体单位排列顺序有关 (1)如果排列顺序与调查内容没有联系，称为按无关标识排列，这时系统抽样估计与简单随机抽样估计效率相仿。 (2)如果排列顺序与调查内容有关，称为按有关标识排列。 按有关标识排列的系统抽样精度一般比简单随机抽样的精度高 (3)案例：上例对汽车尾气排放情况的调查中，是按汽车牌号排列，牌号与尾气排放没有关系，属于按无关标识排列。如果是按汽车价格排列，价格与尾气排放量有相关性，则属于按有关标识排列。在后一种情况下的系统样本中，既有高档汽车，也有低价位的汽车样本的结构与总体的结构十分相似，因而可以有效降低抽样误差。
  • （四）整群抽样
    • 1.概念：是将总体中所有的基本单位按照一定规则划分为互不重叠的群，抽样时直接抽取群，对抽中的群调查其全部的基本单位，对没有抽中的群则不进行调查。
    • 2.优点 (1)实施调查方便，可以节省费用和时间 (2)抽样框编制得以简化
    • 3.缺点：由于抽取的样本单位比较集中，群内各单位之间存在相似性，差异比较小，而群与群之间的差别往往比较大，使得整群抽样的抽样误差比较大。
    • 4.适用：对某些特殊群结构进行调查。
  • （五）多阶段抽样
    • 1.概念：在大规模抽样调查中，一次抽取到最终样本单位是很难实现的，往往需要经过二个或二个以上阶段才能抽到最终单位，这就是多阶段抽样方法。 首先从总体中采用随机方法抽取若干个小总体，称为初级单元；再在这些中选的初级单元中随机抽取若干个单位。如果经过二个阶段抽样，抽取到接受调查的最终单位，称为二阶段抽样；如果经过三个阶段才抽取到接受调查的最终单位，称为三阶段抽样，以此类推。所以多阶段抽样是对经过二个及二个以上抽样阶段抽样方法的统称。
    • 2.在大范围抽样调查中采用多阶段抽样的原因 (1)在大范围抽样调查中，往往没有包括所有总体单位的抽样框，或者编制这样的抽样框十分困难。多阶段抽样是分阶段进行的，抽样框也可以分级进行准备。 (2)多阶段抽样是在中选单位中的再抽选，这样就使样本的分布相对集中，从而可以节省调查中的人力和财力。
    • 3.缺点 多阶段的抽样设计比较复杂，不仅涉及如何划分阶段，还包括在每个阶段上应当抽取多大样本量，以及每个阶段的抽样方法。此外多阶段的抽样误差计算也比较复杂。
• 三、估计量和样本量
  • （一）估计量的性质
    • 什么样的估计量是好估计量？下面以不放回简单随机抽样下的总体均值估计为例，介绍几个常用的选择标准。 估计量的无偏性：对于不放回简单随机抽样，所有可能的样本均值取值的平均值总是等于总体均值，这就是样本均值估计量的无偏性。 估计量的有效性：估计量方差越大，说明用可能的样本估计值之间的差异越大，用样本统计量估计总体参数的效率就越低，抽样误差越大。 估计量的一致性：随着样本量的増大，估计量的值如果稳定于总体参数的真值，这个估计量就有一致性，可称为一致估计量。
  • （二）抽样误差的估计
    • 1、以不放回简单随机抽样下均值估计量为例，说明估计量方差的估计方法。 假设从总体的N个单元中按照不放回简单随机抽样方法抽取n个单元作为样本，用，Y1,Y2,...,Yn表示总体关于变量Y的N个观测值，y1,y2,...,yn表示样本中的n个观测值。把样本均值y̅作为总体均值Y̅的估计量，则估计量y̅的方差为V(y̅)=(1-n/n)S²/n，式中S²为总体方差。
    • 2.由上面的估计量方差可以看出： (1)抽样误差与总体分布有关，总体单位值之间差异越大，则 总体方差S²越大，抽样误差越大。 (2)抽样误差与样本量n有关，在其他条件相同情况下，样本量越大，抽样误差就越小。 (3)抽样误差与抽样方式和估计量的选择也有关系。 利用有效辅助信息的估计量也可以有效地减少抽样误差。 实践中，总体方差S²是未知的，可以利用样本方差来估计，因此估计量方差的估计公式为V(y̅)=(1-n/N)s²/n 式中。s²为样本方差。
  • （三）样本量的计算
    • 1.通常情况下，样本中所含的样本单位数量增大，相应样本估计量的抽样误差会较小，实际应用中，样本量的确定主要考虑以下因素： (1)调查的精度，同向。调查的精度是指用样本数据对总体进行估计时可以接受的误差水平。 (2)总体的离散程度，同向。方差越大，离散程度越大。 (3)总体的规模，对于小规模的总体，总体规模越大，样本也要随之增大（但非同比例）。 (4)无回答情况，若无回答率较高，样本要大ー些。 (5)经费的制约，样本量是经费和精度的折中。 (6)调查的限定时间及实施调查的人力资源。
    • 不考虑费用限制无回答情况及其他影响因素时，简单随机抽样的烊本量计算公式为：
    • p
      • n0为有放回随机抽样样本量
    • p
      • n为不放回随机抽样样本量
    • μα=1.96(在置信度（1-α)为95%的值） 假定待估计的总体比例在0.5附近，总体规模(N)为1000万个，当绝对允许误差分别为0.01、0.03、0.05时，简单随机抽样所需要的样本量分别为9604、1068、385。随着样本量的增大，增加同等样本量所增加的精度幅度呈下降趋势。 1.96*1.96*[0.5*(1-0.5)]/0.01*0.01=9604
• 中级经济师-《经济基础知识》 （共140分，84分及格）
  • 第一部分 经济学基础（10章=29分）
  • 第二部分 财政（7章=23分）
  • 第三部分 货币与金融（5章=23分）
  • 第四部分 统计（5章=21分）
    • 第23章 统计与统计数据
    • 第24章 描述统计
    • 第25章 抽样调查
    • 第26章 回归分析
    • 第27章 时间序列分析
  • 第五部分 会计（5章=21分）
  • 第六部分 法律（5章=23分）