导图社区 英语词性
- 59.8k
- 2.4k
- 579
- 举报
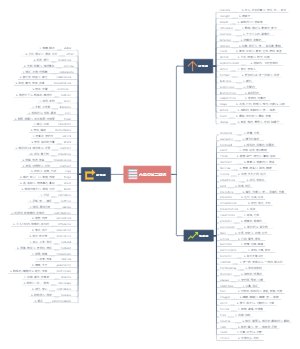
英语词性
词类又叫词性,英语单词根据其在句子中的功用,可以分成十个大类。前六类叫实词,后四类叫虚词。让我们跟着思维导图一起来学习十大类英语词性以及其细分用法分类讲解吧!
编辑于2018-09-08 02:25:51- 英语词性
- 患者宜吃的水果
水果营养丰富,世人皆知.然而,吃水果也有讲究,如果吃得不当反而有害。对患者而言,吃水果更要谨慎,这份思维导图快收好!本思维导图为大家整理了适合各类患者吃的水果分类,喜欢的小伙伴可以点个赞哦!
- 英语词性
词类又叫词性,英语单词根据其在句子中的功用,可以分成十个大类。前六类叫实词,后四类叫虚词。让我们跟着思维导图一起来学习十大类英语词性以及其细分用法分类讲解吧!
- 妈妈必读:一张0-1岁孩子认知发展的精确时间表
儿童心理学,是按照孩子的年龄时间轴来划分的,这就意味着不同时间段可以采取不同的养育参考方案,这也是我们提倡的,正确的时间做正确的事。 今天要给所有妈妈们提供一张0-1岁孩子认知发展的精确时间表。
英语词性
社区模板帮助中心,点此进入>>
- 患者宜吃的水果
水果营养丰富,世人皆知.然而,吃水果也有讲究,如果吃得不当反而有害。对患者而言,吃水果更要谨慎,这份思维导图快收好!本思维导图为大家整理了适合各类患者吃的水果分类,喜欢的小伙伴可以点个赞哦!
- 英语词性
词类又叫词性,英语单词根据其在句子中的功用,可以分成十个大类。前六类叫实词,后四类叫虚词。让我们跟着思维导图一起来学习十大类英语词性以及其细分用法分类讲解吧!
- 妈妈必读:一张0-1岁孩子认知发展的精确时间表
儿童心理学,是按照孩子的年龄时间轴来划分的,这就意味着不同时间段可以采取不同的养育参考方案,这也是我们提倡的,正确的时间做正确的事。 今天要给所有妈妈们提供一张0-1岁孩子认知发展的精确时间表。
- 相似推荐
- 大纲
英语词性
叹词 - int. (interjection)
Examples
My God, ouch, well, hey, er etc.
Use
It often stands alone, unconnected to a sentence.
A short word or phrase that shows emotion.
可数名词 - num. (numeral)
Fractions and demicals
Examples
1/6 is read as "one sisth"
Dates
Multiplicative adverbs
Examples
Once, twice, thrice
Use
Express how many times some event happens
Cardial numbers
Examples
Zero, one, two, three
Use
Refer to the size of a group.
Ordinal numbers
名词 - n. (nouns)
Compound nouns
Examples
football
mother-in-law
bus stop
Use
Acts as a single unit and can be modified by adjectives and other nouns.
Collective nouns
Examples
boss
family
Rule
Can be treated as singular or plural.
Use
It denots a group of individuals.
Countable / Uncountable nouns
Uncountable nouns
Examples
what
electricy
money
Use
Uncountable nouns are always singular.
Yot cannot count uncountable nouns.
Countable nouns
Examples
10 years
A dog
Six dollars
Use
Count nouns have singular and plural forms.
You can count countable nouns
Uncountable nouns
Examples
money
music
love
Use
uncountable nouns are substances, concepts etc that we cannot divide into separate elements. We cannot "count" them.
Countable nouns
Examples
animal-animals
woman-women
man-men
Use
Have both sigular and plural forms
Nouns that can be counted
Proper / Common nouns
Common nouns
Examples
Sub Topic
Book
Dog
Use
Refer to people, places in general
Proper nouns
Examples
November
Italy
Mary
Use
Refer to names of specific people, places or organizayions.
Common nouns
Examples
computer
apple
pen
Use
Common nouns can be countable or uncountable, singular or plural
Common nouns are words for people, places or things that are not specific ( opposed to peoper nouns)
Proper nouns
Examples
St.Paul's Cathedral
America
Cindy
Use
Proper nouns are the names of specific people or places. They should always begin with a capital letter.
动词 - v. (verb)
Auxiliary
Examples
I am eating
Use
A verb used with main verbs to show tense, etc. and to form questions and negatives.
Participle
Past
Forms like wanted, broken, started, begun etc.
Present
Often refered to as the "-ing" form of a verb, such as singing, swimming
Modal
Linking verb
Examples
I feel unwell.
Mary is a nurse.
Use
Link the subject to a noun or adjective.
Link two parts of a sentence.
Have NO object.
Full verb
Intransitive verb
Take NO subject.
The bomb exploded in the city center.
Transitive verb
Take an object.
Examples
Jenna brings Mrs. Smith lunch every day.
连词 - conj. (conuunction)
Subordinating conjunctions
Examples
After, although, because, if, until etc.
Sam went swimming although it was raining.
Use
Used to join a subordinate (dependent) clause to a main (independent) clause.
Coordinating conjunctions
Examples
And, but, or, nor, for, yet, so
I like tea and coffee.
Use
Used to join two parts that are grammatically equal or similar.
介词 - prep. (preposition)
Phrase prepositions
Examples
Because of, with regard to, on behalf, for the sake of etc.
Participle prepositions
Examples
Concerning, notwithstanding, considering etc.
Double prepositions
Examples
Out of, outside of, from beneath etc.
Compound prepositions
Examples
Without, within, inside, outside, into, behind
Simple prepositions
Examples
In, on, at, aboue, over, under,of etc.
冠词 - art. (article)
Types
Indefinite article
an
Example
Please hold me an autobiobiography.
Use
It precedes a word that begins with a vowel.
a
Example
Please hand me a book.
Use
It precedes a word that begins with consonant.
Definite article
the
Example
Are you going to the party this weekend?
Use
To limit the meaning of a noun to one particular thing.
Use
Uded to define a noun as specific or unspecific.
副词 - adv. (adverb)
Types
Degree
Example
She entirely agrees with him.
Time
Example
He came yesterday.
Place
Example
Please sit here.
Manner
Example
He speaks slowly.
Use
Used to modify a phrase, clause or sentence.
Used to modify a verb, an adjective or another adverb;
形容词 - adj. (adjective)
Superlative adjective
Examples
Justin Bieber in the most popular singer in Canada.
Mount Everest is the highest mountain in the world.
Use
Used to describe the extreme quality of one thing in a group of things.
Comparative adjective
Examples
I want to have a more powerful computer.
Chris is taller than John.
Use
Used to describle the difference between two things
Adjective
Examples
A dark sky
An interesting story
A green car
Use
Used to describle a person or thing.
代词 - pron. (pronoun)
Indefinite pronoun
All, another, any, anybody/anyone,anything,each, everybody/everyone, everything, few, many, nobody, none, one, several, some, somemody, someone,etc.
Examples
They lost everything in the earthquake.
Can anyone answer this question?
Use
It is vague and " not definite".
An indifinite pronun does not refer to any specific person, thing, or amount.
Conjuctive pronoun
Relative pronoun
Who, Whom, Whose, Which, That
Examples
The person whose phone just rang should stand up.
The person that phoned me last night is my teacher.
Use
Related to the word that its relative clause modifies.
Used to introduce a relatice clause.
Interrogative pronoun
Who, Whom, What, Which, Whose
Examples
What do you want?
Who told you?
Whom did you tell?
Use
Represents the thing that we don`t know.
Used to ask queations.
Reciprocal pronoun
Each other, One another
Examples
The gangsters were fighting one another.
John and mary love each other
Use
Used when each of two or more subjects is acting the same way towards the other.
Reflexive pronoun
Plural
Themselves
Yourselves
Ourselves
Singular
Himself / Herself / Itself
Yourself
Myself
Use
End in "-self" (singular) or "selves" (plural).
Used to refer back to the sentence or clause
Demonstrative pronoun
Plural
Those
far in distance or time
These
Singular
That
This
near in diatance or time
Use
To show, indicate or point to a thing or things.
Posessive pronoun
Nominal possessive pronoun
Theirs
Yours
Ours
His / Hers / Its
Yours
Mine
Adjectival possessive pronoun
Their
Your
Our
His / Her / Its
Your
My
Use
Show ownership replace noun phrases
Personal pronoun
Object
Them
You
Us
Him / Her / It
You
Me
Subject
They
You
We
He / She / It
You
I
Use
Represent people, places or things