Functions and Graphs-1

Functions and Graphs-1思维导图，讲述了Function、Lines、Graphs of Equations等，希望对你有所帮助！

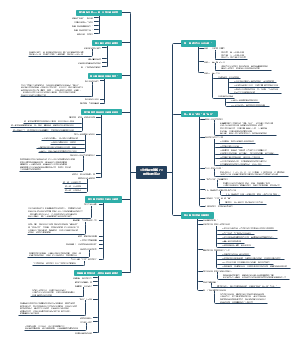
Functions and Graphs

• Function
  • dinition of function
    • A function f from a set D to a set E is a correspondence that assigns to each element x of D exactly one element y of E
    • The element x of D is the argument of f. The set D is the domain of the function. The element y of E is the value of f at x (or the image of x under f) and is denoted by , read “f of x.” The range of f is the subset R of E consisting of all possible values for x in D.
      • The element x of D is the argument of f. The set D is the domain of the function. The element y of E is the value of f at x (or the image of x under f) and
      • is denoted by , read “f of x.” The range of f is the subset R of E consisting
      • of all possible values for x in D.
  • definition oa graph of a function
    • The graph of a function f is the graph of the equation for x in the domain of f.
  • vertical line teast
    • The graph of a set of points in a coordinate plane is the graph of a function if every vertical line intersects the graph in at most one point.
  • types
    • linear function
      • The letter r, which represents an arbitrary number from the domain of f, is called an independent variable.
      • The letter A, which represents a number from the range of f, is a dependent variable, since its value depends on the number assigned to r. If two variables r and A are related in this manner, we say that A is a function of r. In applications, the independent variable and dependent variable are sometimes referred to as the input variable and output variable
    • alternative function
      • A function with domain D is a set W of ordered pairs such that, for each x in D, there is exactly one ordered pair in W having x in the first position.
  • shifting the graph
  • Compressing or Stretching the function
  • Standard Equation of a Parabola with Vertical Axis
    • The graph of the equation for a not equals to 0 is a parabola that has vertex and a vertical axis. The parabola opens upward if a>0
  • Theorem for Locating the Vertex of a Parabola
  • Theorem on the Maximum or Minimum Value of a Quadratic Function
• operation on functions
  • function
    • Functions are often defined using sums, differences, products, and quotients of various expressions
  • composite function
  • theorem for locating the vertex of a parabola
  • types
    • A function f is a polynomial function if is a polynomial—that is, if
    • where the coefficients , , . . . , are real numbers and the exponents are nonnegative integers. A polynomial function may be regarded as a sum of functions whose values are of the form , where c is a real number and k is a nonnegative integer. Note that the quadratic functions considered in the previous section are polynomial functions.
    • An algebraic function is a function that can be expressed in terms of finite sums, differences, products, quotients, or roots of polynomial functions.
• Lines
  • slope of a line
    • Let l be a line that is not parallel to the y-axis, and let p1(x1,y1) and p2(x2,y2) be distinct points on l. The slope m of l is
    • (a) the slope is positive, and we say that the line rises. In Figure 1(b) the slope is negative, and the line falls
    • point slope form for the equation of a line
    • slope intercept form fot the equation of a line
    • theorem on slopes of perpendicular lines
      • Two lines with slope and are perpendicular if and only if m1m2 = -1
  • general form for the equation of a line
    • The graph of a linear equation ax+by = c is a line, and conversely, every line is the graph of a linear equation.
• Graphs of Equations
  • about equation and graph
    • Two quantities are sometimes related by means of an equation or formula that involves two variables.
      • Two quantities are sometimes related by means of an equation or formula
      • that involves to variables.
    • an ordered pair (a,b) that yields a true statement if x=a and y=b.
  • sketching a simple graph by plotting points.
    • It is convenient to list coordinates of several such points in a table, where for each x we obtain the value for y
    • Ordinarily, the few points we have plotted would not be enough to illustrate the graph of an equation; however, in this elementary case we can be reasonably sure that the graph is a line.
    • the end behavior—the pattern of the graph as x assumes large positive and negative values (that is, the shape of the right and left ends)—is apparent to the reader. For written work, we use arrow notation from the following chart when describing functions and their end behavior
      • the
      • end behavior—the pattern of the graph as x assumes large positive and negative values (that is, the shape of the right and left ends)—is apparent to the
      • reader. For written work, we use arrow notation from the following chart
      • when describing functions and their end behavior
    • The graph in Figure 2 is a parabola, and the y-axis is the axis of the parabola. The lowest point is the vertex of the parabola, and we say that the parabola opens upward
    • how to find x and y intercepts
      • when we are finding x intercepts, we let y equals to zreo and calculate x intercept using the equation.
      • take the same step to find y intercepts.
    • symmetric
      • a graph that is symmetric with respect to the x-axis
        • ex. y square = x
        • Since substitution of for y does not change the equation, the graph is symmetric with respect to the x-axis
      • graph symmetric with respect to the origin
        • If we simultaneously substitute for x and for y, the equation is still the same.
    • circle
      • Standard Equation of a Circle with Center (h, k) and Radius r
      • In some applications it is necessary to work with only one-half of a circle—that is, a semicircle. The next example indicates how to find equations of semicircles for circles with centers at the origin.
• Rectangular Coordinate Systems
  • What is coordiante systems
    • fored by twocootdinate acesthat intersect at the origin O
    • also called xy-plane
    • divided into four quadrants; first, second, third, and fourth quadrants, labeled I, II, III, and IV
  • formula
    • distance formula
      • The distance between any two points and in a coordinate plane
    • midpoint formula
      • The midpoint M of the line segment from to is