导图社区财务管理基础

财务管理基础

轻松学中级财务管理第二章财务管理基础知识梳理，包括货币时间价值、风险与收益、成本性态分析等等。

编辑于2022-11-20 00:13:02 广东

中级财管
中级会计
财务管理基础

张沛棋

他的近期作品查看更多>>

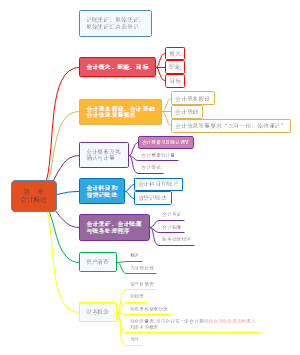
00、2023财管考纲变化分析和目录
关于00、2023财管考纲变化分析和目录的思维导图，调整教材章节顺序：将原第6章“债券、股票价值评估”调至第三章《价值评估》，放在第4 章《资本成本》之前。调完之后，先从投资者角度讨论“债券、股票估值”问题，再从筹资者角度讨论“资本成本”问题。
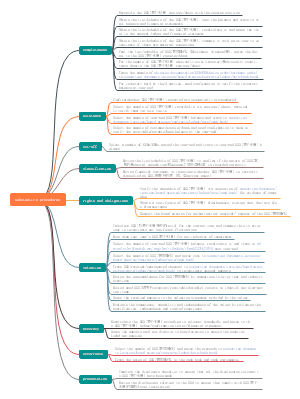
2023CPA考试重难点收入章节的总结
《收入》在CPA考试中占将近20分在考试或者在实务中都是重中之重，难度比长投和金融工具章节小，建议把分值拿下。本图整理的收入概念、确认与计量、合同成本、特定交易、PPT项目、费用、利润、科目的知识点都要吃透，学习开始吧！
第六章债券和股票价值评估（2022.12.06）
关于第六章债券和股票价值评估（2022.12.06）的思维导图。导图主要从本章框架、债券价值评估、普通股值评估、混合筹资工具几个方面作了介绍。

财务管理基础

社区模板帮助中心，点此进入>>

张沛棋

他的近期作品查看更多>>

相似推荐
大纲

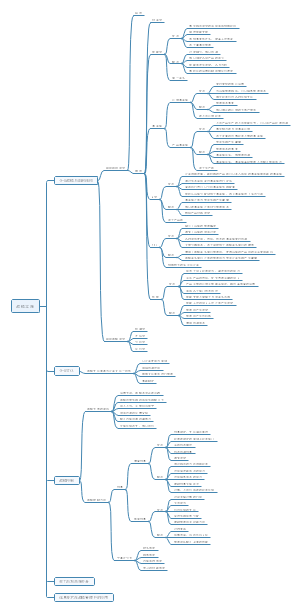
CPA战略风险管理、战略实施
- 2.3k
- 1
- 83
- 8
13501805163
substantive procedures
- 817
- 1
- 14
- 0
诗月云间
初级会计实务第一章
- 1.4k
- 0
- 44
- 3
阑珊
会计科目
- 1.5k
- 102
- 104
- 14
Jarvis
增值税法思维导图
- 1.6k
- 30
- 87
- 7
徐灰灰
第六章合同的保全
- 435
- 3
- 24
- 3
早安兮
固定资产
- 1.0k
- 20
- 80
- 8
阑珊
初级会计实务第二章：存货
- 1.0k
- 13
- 109
- 8
阑珊
初级会计实务思维导图
- 1.8k
- 164
- 219
- 45
飞奔的小马
应收及预付款项
- 1.0k
- 12
- 79
- 12
阑珊

第二章财务管理基础

第一节：货币时间价值

1.1、货币时间价值的概念

货币时间价值：在没有风险、没有通货膨胀的前提下，货币经历一定时间的投资和再投资，所增加的的价值，就是货币时间价值

无风险

无通货膨胀

纯利率=资金市场的平均利率

短期国债利率，属于无风险利率，在没有通货膨胀的情况下，它就是纯利率

经历一定的时间

投资再投资

增加的价值部分

复利：就是利滚利，它计算利息的基础是本金+前期累计的利息和

单利：每期利息的计算基础都是对应的本金

1.2、复利终值与现值

1.2.1、复利终值与现值的公式：

P：现值

i：利率/报酬率（对应次数N的利率）

n：次数

利率和期数要口径一致

F：终值

复利终值系数：

1元的复利终值

用符号（F/P，i，n）表示

（F/P，6%，3）=1.191

复利终值系数表

P=1元是已知的，那么F，i，n，知其2能求另外一个1

复利终值的计算：F=P*（F/P，i，n）

复利现值的计算：F=P*（F/P，i，n）→P=F÷（F/P，i，n)→P=F*(P/F，i，n）

除过来

复利终值系数和现值系数，互为倒数

(F/P,I,N)*(P/F,I,N)=1

所以知道复利终值系数，就可以同时求F或者P

例题：某人将100元存入银行，年利率是4%，半年计息一次，按照复利计算，5年后的终值是多少？(F/P,2%,10)=1.219

P=100元

N=5年*2次/年=10次

I=4%÷2=2%

F=？

F=P*(F/P,I,N)=100*(F/P,2%,10)=100*1.219=121.90元

1.3、普通年金终值与现值

1.3.1、关于年金-A

年金的定义：连续等额等间隔

连续：多笔，次数大于1

等额：每期的金额相等

等间隔：每期的时间段相等

年金的分类：

普通年金：等额的现金流收付时间点，从第1期的期末开始

例如存款的利息，都是每年的年末才付，当年的利息

预付年金：等额的现金流收付时间点，从第1期的期初开始

例如房租的租金，都是每月的月初就收，当月的租金

递延年金：等额的现金流收付时间点，从第m期的期末开始

例如教育金，现在交钱，等小朋友上大学时，每年领取同样的教育金，合计领取4年，合同结束

永续年金：等额的现金流收付时间点，从第1期的期末开始，永久收付，N无穷大

例如永续型的养老保险，现在交钱，60岁以后，每个月收到一笔同样的养老金，直到被保险人人死亡为止

1.3.2、普通年金终值的计算

普通年金终值的定义

普通：现金流的收付时间点，从第1期的期末开始

年金：连续等额等间隔，期数大于1，金额相等，时间段相等

终值：未来的价值

普通年金终值的计算公式：F=A*(F/A,I,N)

（F/A,I,N）普通年金终值系数

例题：从今年开始，每年的年末都存10000元进银行，银行利率10%，请问第3年的年末，我有多少钱在银行？

今年的年末：普通

每年都存10000元：年金

第3年年末有多少钱：终值

普通年金终值计算，F=A*(F/A,I,N)=10000×（F/A，10%，3）=10000×3.31=33100元（本金3万，利息3100元，比单利3000元要多）

1.3.3、普通年金终值的计算（偿债基金）

偿债基金：普通年金的年金计算：F=A*(F/A,I,N）→A=F÷（F/A,I,N）→A=F*(A/F,I,N)

例题：拟在5年后还清10000元的债务，从今年年末开始，每年存入银行一笔钱，银行年利率10%，每年存多少？

判断是普通年金

知道终值，利率，期数

求年金A

F=A*(F/A,I,N)→A=F÷(F/A,I,N)=10000÷（F/A，10%，5）=10000÷6.105=1638元（本金1638*5=8190，利息1810，合计10000）

1.3.4、普通年金现值的计算

普通年金现值的定义

普通：现金流的收付时间点，从第1期的期末开始

年金：连续等额等间隔，期数大于1，金额相等，时间段相等

现值：现值的价值，折现

普通年金现值的计算公式：P=A*(P/A,I,N)

（P/A,I,N）普通年金现值系数

例题：从今年开始，每年的年末我都要捐1万元给贫困山区，连续捐3年，如果我从年初一次性存多少钱进银行，能满足我的捐款节奏？银行年利率10%

今年开始，每年年末，都捐1万，判断是普通年金

知道年金1万，期数3年，年利率10%，求P

P=A*(P/A,I,N)=10000*（P/A，10%，3）=10000×2.4868=24868元（本金比总捐款3万少，因为有利息）

1.3.5、普通年金年金的计算（投资回收系数）

投资回收系数：普通年金的年金计算：P=A*(P/A,I,N）→A=P÷（P/A,I,N）→A=P*(A/P,I,N)

例题：现在跟银行贷款20万元，年利率10%，投资一个10年项目，那么这个项目每年末收回多少钱，我的投资才不会亏钱？

今年开始，每年年末，都收回一笔等额的钱，判断是普通年金

知道现值，期数，年利率，求每年收回的年金

P=A*(P/A,I,N)→A=P÷(P/A,I,N)=200000÷（P/A,10%,10）=20000÷6.1446=3254元（共收回32540，其中12540刚好够支付借款利息）

1.4、预付年金终值与现值

1.4.1、预付年金的理解

预付：现金流的收付在第1期的期初

年金：连续等额等间隔

1.4.2、预付年金终值的计算

F预=A×[（F/A,I,N+1)-1]

加1期，所以减1

F预=A×（F/A,I,N）×（1+I）

预付年金终值比普通年金终值多收一个（1+I）

A=100,I=8%,N=6

普通年金终值，F=A*(F/A,I,N)=100*(F/A,8%,6)

普通的终值小

预付年金终值，F=A*[(F/A,I,N+1)-1]=100*[(F/A,8%,7)-1]

预付年金终值，F=A*(F/A,I,N)*(1+I)=100*(F/A,8%,6)*(1+8%)

预付的终值大（1+I)

1.4.3、预付年金现值的计算

P预=A×[(P/A,I,N-1)+1]

少1期累计，所以加1

P预=A×(P/A,I,N)*(1+I)

预付年金现值比普通年金现值多付一个（1+I）

A=200,I=10%,N=6

普通年金现值，P=A*(P/A,I,N)=200*(P/A,10%,6)

普通的现值小

预付年金现值，P=A*[(P/A,I,N-1)+1]=200*[(P/A,10%,5)+1]

预付年金现值，P=A*(P/A,I,N)*(1+I)=200*(P/A,10%,6)*(1+10%)

预付的现值大(1+I)

预付年金的关键词

每年年初/每月月初

1.5、递延年金终值与现值

1.5.1、递延年金的理解

递延：现金流的收付在第2期或第2期以后的期末

年金：连续等额等间隔

终值：未来的价值

现在：现在的价值，折现

P现值；F终值；I利率；N年金期数，M递延期数，A年金

1.5.2、递延年金的终值

跟普通年金的终值类似，找出正确的期数N即可（与递延期数M无关）

递延年金终值的计算公式：F=A*(F/A,I,N)

1.5.3、递延年金的现值

方法1：二次折现法

第一步：算普通年金的现值Pn

第二步：将普通年金的现值Pn作为终值，再折现到P0

例题：

1||| 第一步：求普通年金现值P3=A*(P/A,I,N)=100*(P/A,10%,4)=100*3.170=317元

2||| 第二步：将普通年金现值P3作为终值F3，再折现到现值P0=F*(P/F,I,N)=317*(P/F,10%,3)=317*0.7513=238.16元

方法2：现值相减法

第一步：算全部期间的普通年金现值P(m+n)

P(m+m)=A*(P/A,I,M+N)

P(3+4)=100*(P/A,10%,3+4)=100*4.8684=486.84元

第二步：算递延期间的普通年金现值Pm

Pm=A*(P/A,I,M)

P3=100*(P/A,10%,3)=100*2.4869=248.69元

第三步：算递延年金现值Pn

Pn=P(m+n)-Pm

P4=P(4+3)-P3=486.84-248.69=238.15元

1.6、永续年金现值

1.6.1、永续年金的理解

1、永续：领取的期数无穷大，永远领取下去

2、年金：连续等额等间隔

3、终值：因为期数无穷大，所以永续年金无终值

4、现值：现值的价值，折现

永续年金类似存本取息：我现在存入本金，每年固定领取利息，本金133元不取，利息（每季度2元）不断

1.6.2、永续年金-无终值

永续年金没有终止的时间，所以没有终值

1.6.3、永续年金的现值

P永续=A÷I

例子1：优先股1股，每个季度发放利息2元，年利率6%，那么对应合理的优先股的价格（现值）

P=A÷I，这里的A是2元，对应的I是6%÷4=1.5%，所以P=2÷1.5%=133.33元

我现在花了133.33元买这个优先股，每个季度拿到2元，每年股息就是8元，计算每年的利率=8元÷133.33元=6%，跟承诺有保底

1.7、利率的计算

1.7.1、查表法

简单，直接查表，而且考试无法出题

1.7.2、已知现值或终值系数，求利率-内插法-信用卡分期

例题：已知(P/A,I,5)=4.20，求利率I，查表在期数为5的行中，没有找到4.20数值的，不过找到相邻的两个数值4.2124（6%）和4.1002（7%）

7%-I

4.1002-4.2000

7%-6%

4.1002-4.2124

原则：具有对应关系的数字在等式两边的位置相同

通过解公程式，得出I=6.11%

1.7.2、未知现值或终值系数，求利率-内插法

例题：已知(P/A,I,5)=4.20，求利率I，查表在期数为5的行中，没有找到4.20数值的，不过找到相邻的两个数值4.2124（6%）和4.1002（7%）

4%-I

108.11-104

4%-5%

108.11-100

原则：具有对应关系的数字在等式两边的位置相同

通过解公程式，得出I=4.51%

1.7.3、名义利率和实际利率（1年多次计息，复利的影响）

一年多次计息时

给出的年利率，是名义利率（报价利率）

按复利计算的利息÷本金的比值，是实际利率（有效年利率）

公式：

M=计息次数

M的次数越多，有效年利率就越大于报价利率

M=1时，有效年利率=报价利率

1.7.4、名义利率和实际利率（通货膨胀影响）

公式：

通货膨胀率＞名义利率时，实际利率为负

存钱贬值了

通货膨胀率＝名义利率时，实际利率为0

存不存钱都一样

通货膨胀率＜名义利率时，实际利率为正

存钱，还能小赚一笔

1.8、本节总结

1.8.1、互为倒数的组合

1||| 复利终值系数和复利现值系数

（F/P,I,N）

（P/F,I,N）

2||| 普通年金终值系数和偿债基金系数

（F/A,I,N）

（A/F,I,N）

3||| 普通年金现值系数和投资回收系数

(P/A,I,N）

（A/P,I,N）

特点，前面两个字母对调位置，就是互为倒数

1.8.2、利率的计算类型

1||| 已知终值或现值系数，用内插法求利率

2||| 已知公式的结果，用内插法求利率

3||| 一年多次计息（复利）下，计算名义利率（报价利率）或实际利率（有效年利率）

记住公式

4||| 通货膨胀影响下，计算名义利率和实际利率，或通货膨胀率，3者知其2能求未知1

记住公式

第二节：风险与收益

2.1、资产收益与收益率

2.1.1、收益率概念的理解

1||| 实际收益率

已经实现或者确定可以实现的资产收益率

实际收益率=利息率+资本利得收益率（同时剔除通货膨胀率）

2||| 预期收益率

也叫期望收益率，预测某项资产未来可能实现的资产收益率

3||| 必要收益率

表示投资者对某资产合理要求的最低收益率。

2.1.2、收益与实际收益率

收益=利息股利（利润收益）+资本利得（价差收益）

收益率=（每股股利+每股资本利得）÷期初股价（购买时）

例如我在年初购买A股票100股，股价10元，年中取得分红2元/股，年末我在13.50元全部卖出该股票。这样每股我投入10元，获得2元分红+3.5元价差=5.5元，收益率5.5÷10=55%

2.1.3、期望收益率

预期收益率是指，可能出现的收益与其发生概率作为权重的加权平均值。

A项目的预期收益率=0.2*0.15+0.6*0.10+0.2*0=9%

B项目的预期收益率=0.3*0.20+0.4*0.15+0.3*（-0.10）=9%

2.1.4、必要收益率

必要收益率，投资者要求的最低收益率

必要收益率=无风险收益率+风险收益率

无风险收益率=纯粹利率（货币的时间价值）+通货膨胀补偿率

无风险收益率一般用短期国债利率表示

风险收益率，投资者愿意承担一定的风险（损失），希望获得相应的风险补偿收益

风险的大小

投资者对风险的偏好

总结：必要收益率=纯粹利率+通货膨胀补偿率+风险收益率

2.2、资产的风险及其衡量

2.2.1、风险的定义

风险，不代表损失，而是指预期收益的波动性或不确定性

某证券的收益波动幅度越大，风险越大，也意味着收益越大

国债：收益波动不大，风险小，收益小

债券：收益波动一般，风险一般，收益一般

股票：收益波动很大，风险很大，收益很大

高风险高收益，将会是后续财务管理决策的基础（对风险与收益的衡量与判断）

2.2.2、风险的衡量

1、概率分布

概率是用来表示随机事件发生可能性大小的数值。

例如：抛硬币，正面的概率是50%，背面的概率也是50%

2、期望值

期望值是可能出现的收益和发生概率（作为权重）的加权平均值。

例如：我投资某只股票，有30%的概率，能赚20%，有70%的概率，亏20%，那么这只股票的期望值=0.3*0.2+0.7*（-0.2）=-8%

3、方差、标准差、标准方差

1||| 方差

方差是各个数据与其算术平均数的离差平方和的平均数

2||| 标准差，是方差的平方根

标准差σ 也叫标准离差，一种衡量变量的分布偏离其中值程度的统计指标。

上题的标准差=

=1.4142

标准差以绝对数衡量决策方案的风险，在期望值相同的情况下，标准差越大，风险越大；反之，标准差越小，则风险越小。

由于无风险资产没有风险，所以，无风险资产的标准差等于零

标准差σ=0，风险为0

3||| 标准差率，是方差和期望值的比值

CV=σ÷R'

=标准方差=标准差÷期望值

标准差率是一个相对数指标，它以相对数反映决策方案的风险程度。

4||| 总结区别

期望值相同的方案，方差/标准差越大，风险越大，反之，标准差越小，风险越小

期望值不同的方案，不能用方差和标准差来做决策，只能用标准差率来表示，标准差率越大，风险越大，标准差率越小，风险越小

4、风险衡量的计算步骤

例题：

第一步；计算期望值

项目A的期望收益率=0.2*0.05+0.2*0.1+0.2*0.15+0.2*0.2+0.2*0.25=0.15

项目B的期望收益率=0.15*0.1+0.2*0.2+0.3*0.3+0.2*0.4+0.15*0.5=0.3

第二步：计算方差

第三步：计算标准差

因为A和B项目的期望值不同，所以单纯看标准差，B方案风险更大

第四步：计算标准差率

因为期望值不同，用标准差率来对比更客观，其实A的风险更大

通过以上对风险的衡量，其实决策者是可以做到，低风险高收益的，就是选择标准差率更低，但期望收益率更高的额方案

保守投资者

选择低收益率，同时风险更低的方案

看期望收益率和标准差率

激进投资者

选择高风险，同时收益率更高的方案

看期望收益率和标准差率

普通投资者

在收益率相同的时候，选择风险更低的方案

看标准差

2.2.3、风险矩阵

2.2.4、风险管理的原则

1. 融合性原则

风险管理，要与企业的战略，经营管理，业务流程相适应

2. 全面性原则

全面覆盖

3. 重要性原则

重点风险，重点监控

4. 平衡性原则

权衡风险与回报，成本与收益之间的关系

2.2.5、风险管理的对策

1. 规避风险（直接放弃）

资产风险带来的损失，不能由该风险可能获得的收益予以抵消，应该放弃该资产，以规避风险

损失大于收益

拒绝与不守信用的厂商有业务往来

预测损失大于收益

放弃明显亏损的投资项目

投再多都是打水漂，干脆直接放弃

新产品在测试阶段就发现诸多问题果断停止试制

不生产，等新产品改良后再试制

2. 减少风险（事前控制）

（1）控制风险因素

（2）控制风险发生的频率，以及降低风险的损害程度

风险可控，尽量在事前就预测风险，控制风险

3. 转移风险（转嫁他人）

风险无法规避，自己也无法减少处理，而且对企业会造成毁灭性的打击

付出一定的代价，把风险转移出去给专业的公司处理

1||| 投保保险，把风险转移给保险公司

2||| 采取合资、联营、增发新股、发行债券、联合开发等措施实现风险共担；

3||| 通过技术转让、特许经营、战略联盟、租赁经营和业务外包等实现风险转移。

4. 接受风险（坦然面对）

风险自担

事后处理

风险自担是指风险损失发生时，直接将损失摊入成本或费用，或冲减利润-风险自担

风险矩阵的优点

确定风险等级，可视化

风险矩阵的缺点

1||| 评判的主观性太强，会影响结果的正确性

2||| 风险重要性等级是通过相互对比得出，无法用数学运算得出精确的数字等级

风险自保

事前处理

风险自保是指企业预留一笔风险金（风险自保）或随着生产经营的进行，有计划地计提资产减值准备-风险自保

2.3、证券资产组合的风险与报酬

2.3.1、证券资产组合的预期收益率（简单）

投资组合的预期收益率就是该组合所有证券预期收益率的加权平均值

2.3.2、证券资产组合的风险及其衡量

风险大小的衡量，不能用预期收益率的大小，需要用到资产组合的标准差来判断

组合标准差的影响因素

1、各自的权重占比

2、各资产间的相关性

两项资产的相关性，用相关系数r来表示

r=+1

绝对正相关

我涨多少你跟涨多少

0＜r＜+1

正相关

我涨你也涨，幅度不一样

r=0

不相关

我涨跌多少，你都无动于衷

-1＜r＜0

负相关

我涨你跌，幅度不一样

r=-1

绝对负相关

我涨多少你跟跌多少

投资组合的标准差

（1）、相关系数r=+1时，风险最大，此时无可分散风险！

每种证券的收益率会同方向同幅度的变化