人卫第8版《卫生统计学》——第九章《分类变量的卡方检验》

这是本书的第一个非参数检验方法，要好好学习哦！

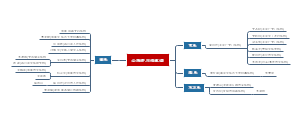
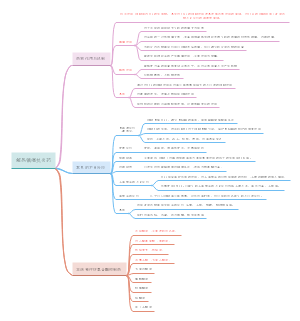
第九章 分类变量的卡方检验

• 前后联系
  • 联系第二章
    • 分类数据交叉表的表达方式
    • 如何采用条件分布来描述分类变量的相关性
  • 联系第七章
    • 单个总体率的统计推断
    • 两个总体率的统计推断
    • 分类数据：事件的总体发生率
  • 本章
    • 基于分布介绍两个或多个率比较的检验、关联性检验、拟合优度检验、Fisher确切概率方法
  • 本章逻辑
    • 两组或多组分类变量的统计分析
      • 卡方检验的基本思想
        • 卡方检验的应用
          • 率的比较
            • 样本量足够
              • 互相独立数据
                • 2×2
                • R×C
              • 配对设计数据
                • 2×2
                • R×R
            • 样本量较小
              • Fisher确切概率法
          • 独立性（关联性）检验
          • 拟合优度检验
    • 卡方检验是针对两组或多组分类变量的总体率或总体频数分布进行推断的方法
      • 结合第七章中（单个或）两个总体率的近似z检验，进行对比理解
• 卡方检验的基本思想
  • 卡方检验=Pearson 卡方检验
  • 卡方统计量
    • 四格表
      • Aij为实际频数：即研究中实际观察所得的频数
      • Tij为理论频数
      • nR1与nR2为四格表的行合计
      • nC1与nC2为四格表的列合计
  • 基本思想
    • 1、统计量之间差别产生的原因，或者是因为来源于同一总体的抽样误差，或者是因为不同总体的本质差别。
    • 2、理论频数计算前提：在H0成立的前提下，按照合并的样本率估算，各组应分配的平均频数
    • 3、计算卡方统计量：所有格子的实际频数和理论频数之差的差异
      • 自由度的计算公式：v=（行数-1）×（列数-1）
    • 4、卡方分布是一种连续型随机变量的概率分布，自由度v是其唯一参数，记为
    • 5、若H0成立，那么两个样本之间的差别可认为由抽样误差所致，则理论频数A与实际频数T之间的吻合程度应该越高，卡方值不会太大
    • 6、卡方检验的基本思想实质：将对两个或多个总体率（构成比）的比较转化为实际频数与理论频数吻合程度的比较
  • 适用情况
    • 针对两组或多组分类变量的总体率或总体频数分布进行统计推断
    • 了解两组或多组样本的总体率（或构成比）之间是否具有统计学意义
• 卡方分布的性质
  • 分布可以看作一种特殊的抽样分布
    • 设有k个互相独立的随机变量Z1、Z2，……，Zk，其服从均数为0，标准差为1的标准正态分布，则服从自由度为v（v=k）的分布，记为
  • 分布是一簇连续光滑曲线，不同的自由度决定卡方曲线的形状各有不同。单峰
    • 牵涉到连续型校正
    • 1、当自由度较小时，卡方分布越为偏斜，随着v取值的增大，曲线逐渐趋于对称，当v趋于∞时，卡方分布将逼近正态分布
    • 2、各种自由度取值下卡方分布右侧尾部面积（概率）为α时的临界值记为
      • 单侧界值
    • 3、当v=1时，卡方（0.05,1）=3.84
  • 分布的期望值（均值）为自由度v，方差为2v
    • 明显地，随着自由度v的增大，卡方分布将随着均值v的增大向数周右侧延展，而分布曲线也将随反差的增大而越趋低阔
  • 卡方检验的基本思想实质：将对两个或多个总体率（构成比）的比较转化为实际频数与理论频数吻合程度的比较
    • 二分变量对应率的概念，多分类变量对应构成比的概念
  • 补充：如果随机变量Z服从标准正态分布，那么其平方将服从自由度为1的卡方分布（赵耐青版P57)
• 率的比较
  • 2×2交叉表（四格表）的卡方检验
    • 相互独立
    • 假设检验步骤
      • 1、建立检验假设，确定检验水准 H0：总体检出率相同 H1：π1≠π2 α=0.05
        • 只能进行双侧检验
      • 2、计算检验统计量：
      • 3、确定P值，作出推断
        • 单侧界值（同方差分析的进行双侧检验但查单侧界值）
    • 严格的适用条件
      • 卡方检验本质是将连续型变量的分布用于分类变量的推断，故四格表卡方检验的基本公式和专用公式均有着较为严格的适用条件
      • 若n≥40，且任意一个格子的理论频数Tij≥5，可直接使用
      • 若n≥40，但出现1个格子的理论频数1≤Tij＜5，则需要对卡方值进行连续性校正
      • 若n＜40或者任意一个格子的理论频数Tij＜1，则卡方检验不在适用，宜采用Fisher确切概率法进行处理
        • 第五节中介绍
  • 两个率的z检验和卡方检验的区别和联系
    • 联系
      • 都可以检验两个率之间的差别，且都基于零假设应用了合并率的概念（Pc和Tij）
      • 两种检验的应用条件均满足时两者等价，即z²=卡方²
      • 都存在连续性校正问题
        • 因为率属于离散型随机变量，但是Z分布和卡方分布都是连续型分布
    • 区别
      • 率的Z检验可按研究设计进行单侧或双侧假设检验，卡方只能进行双侧检验（单侧界值）
      • 率的Z检验只能检验两个率之间的差别，卡方检验能检验两个或多个率的差别
      • 率的Z检验可以计算两个率之差的95%置信区间，以分析两率间有无实际意义，卡方检验用于2×2列联表资料有无关联的分析
  • R×C交叉表的卡方检验
    • 推断3个以上的总体率（或构成比）之间的差异
    • 基本原理和计算步骤与2×2交叉表类似
    • 与2×2交叉表不同之处在于
      • 一般地，理论频数Tij的公式可泛化为下式
        • n为总例数，nRi为第i行的合计数，nCj为第j列的合计数
      • 可直接使用下式计算卡方统计量
        • 自由度v=（R-1）×（C-1）
      • 检验假设与检验结论有所区别
        • 详见后述，卡方分割
    • 注意
      • R×C交叉没有校正公式，若理论频数过小，或1/5以上格子的理论频数小于5，则要考虑合理合并行或列，或增加样本量
      • 若有一个格子的理论频数小于1，则采用Fisher确切概率法
    • 多个构成比的比较
      • R≥2，C＞2
      • 假设检验步骤
        • 1、建立检验假设，确定检验水准 H0：分布是否相同 H1： α=0.05
        • 2、计算检验统计量：
        • 3、确定P值，作出推断
    • 多个率的比较
      • R≥2，C=2
      • 1、建立检验假设，确定检验水准 H0：总体率是否相同 H1： α=0.05
    • 分割
      • 多个率或多个构成比比较的卡方检验，当结论为拒绝H0时，仅代表总的来说多组之间是有差别的，即至少由两组的总体率或频率分布时不同的，但不意味着任意两组之间均有差异
      • 若需明确哪两组之间存在差异，可做率的多重比较，即进行卡方分割
      • 做法：将R×C表分割为若干个小的四格表进行检验
      • 条件：要根据比较次数合理地修正检验水准α，否则将人为地增大犯Ⅰ类错误地概率
        • 结合多个均数两两比较中采用的Bonferroni法进行理解
        • α'=
          • k为需比较的组数
        • 若设置一个共同对照，则只需要进行（k-1)次
      • 注意事项
        • R×C交叉表的卡方检验要求理论频数不宜太小
        • 若理论频数过小，或有1/5以上格子理论频数小于5，应考虑增加样本量，或结合专业知识对行或列进行合并
        • 若出现一个格子的理论频数小于1，应采用Fisher确切概率法，一般采用软件实现计算
  • 适用于完全随机设计的两个或多个率（或构成比）的比较，强调样本的独立性
• 配对设计数据的卡方检验
  • 概述
    • 1、列表的行、列变量是相互关联的，甚至反映的是一个事物的同一属性，常见于配对或配伍组设计。
    • 2、比如：将每个待测标本一分为二，分别采用两种不同方法进行检测，比较两种不同检测方法有无差异；为评价某种处理是否产生作用，测定同一批患者受试前后某项指标的阳性反映
  • 配对四格表的卡方检验
    • 配对四格表通用表格
    • 1、两种变量的结果有无差别就体现在b、c这两个对子数
    • 2、在H0：两种检验方法的阳性概率相同结果成立的条件下，b和c两个格子理论频数都应该为（b+c）/2。当b+c≥40时，可进行简单推导：
    • 3、则配对卡方检验的公式为：
    • 4、类似地，若b+c＜40，则需对式进行连续性校正：
  • 配对R×R交叉表数据的卡方检验
    • 实际工作中，不少分类变量都具有R（R≥）个可能的“取值”，则构成更泛化的配对R×R交叉表。这类研究通常需要解决的问题为，两个样本分布所对应的总体概率分布是否相同。
    • 1、建立检验假设，确定检验水准 H0：两变量的概率分布相同 H1： α=0.05
    • 2、统计检验量为：
      • • k=类别数
        • ni和mi分别为第i行合计和第i列合计
        • Aii=实际频数
      • H0成立时，T统计量服从自由度为k-1的卡方分布
    • 3、确定P值，作出推断
• 独立性检验
  • 基本思想
    • 率的比较 → 仅适用于推断两个或多个独立样本的总体概率（或构成比）相同与否
    • 独立性检验=关联性检验 → 两个或多个分类变量的关联性及其强度（实际工作中，研究者需要了解）
    • 独立随机样本 → 一般地，变量X和变量Y互相独立是指变量X的概率分布与变量Y的概率分布互不相关
    • 交叉分类 → 分类变量的概率分布彼此相关，常见于一份随机样本同时按两种不同属性分类。
    • eg.同一批监测水样两种不同检测结果的关联性、同一批大学生其专业类型与防艾知晓状况之间的关联性
  • 步骤
    • 1、首先针对交叉分类表进行两种属性独立性的卡方检验
    • 2、计算关联系数以描述两个属性之间的关联强度
  • 2×2交叉表的独立性检验
    • 检验过程
      • 1、建立检验假设，确定检验水准 H0：两变量间相互独立 H1：两变量之间相互关联
      • 2、计算检验统计量 → 在H0成立的条件下，该变量应服从卡方分布 → 若拒绝H0，则认为两变量存在关联
      • 3、确定P值，作出推断
      • 4、关联系数的计算
        • • 关联系数采用第二章学习的Pearson列联系数
          • 取值范围[0,1)
    • 注意事项
      • 1、分类变量的关联性分析与率（或构成比）的差异性分析，在检验过程和方法上完全一致
      • 2、但两大类分析在研究目的、设计方案、数据结构与结果解释方面有着本质区别
      • 3、关联性分析，主要针对同一随机样本的两个不同属性变量所形成的交叉表，侧重于推断两个不同属性变量之间存在关联性与否
      • 4、而率（或构成比）的比较，则主要针对两个或多个独立随机样本所形成的交叉表，侧重于推断其分别所代表的总体率（或构成比）之间是否存在差异
      • 区别
    • eg.对某社区n名居民，询问其病史，对其进行体检，收集糖尿病及肥胖情况，分析肥胖与患糖尿病之间是否存在关联性
      • 给出的是同一组研究对象的两个不同属性的概率分布对比，不是两组不同的研究对象
  • 2×2配对数据的独立性检验
    • eg.某医院甲乙两位检验师对同一批血液标本的病毒抗原进行监测，两位检验师的监测结果是否存在关联
    • 步骤同”2×2“交叉表的独立性检验
    • 注意：零假设是数据间相互独立，因此此处的配对数据也直接使用卡方检验公式，而不用配对卡方检验的公式（即含b和c的公式）
      • 与配对设计的率的比较是不同的
  • R×C交叉表的独立性检验
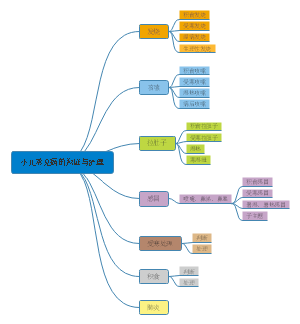
    • eg.比较不同毒害作用与小鼠肝脏脂肪变性的关联性
    • 步骤同”2×2“交叉表的独立性检验
• 拟合优度检验
  • 概念
    • 拟合：分析现有观测变量的分布形态，检查其分布能够与某一期望分布（或标准分布）很好地吻合起来
    • 拟合优度检验=判断实际样本的观察频数分布是否服从某一理论期望频数分布（即用来监测观测数与依照 某种假设或分布模型计算得到的理论数之间一致性的一种统计假设，以便判断该假设或模型是否与实际观测数相吻合）
    • 拟合优度检验又称
      • 吻合度检验：检测观测数与理论数之间的一致性
        • 相当于率的分布
      • 独立性检验：通过检验观测数与理论数之间的一致性来判断事件之间的独立性
        • 相当于上述的独立性检验
  • 基本思想
    • 以拟合正态分布为实例
      • 1、编制频数表，获得样本观测值落在各组段的实际频数Ai
      • 2、根据正态分布的标准转换求出样本落在该组段的概率Pi，利用概率Pi求出对应的理论频数Ti
      • 3、根据理论频数Ti与实际频数Ai的吻合程度，计算卡方统计量，确定P值，作出结论
  • 计算步骤
    • 1、计算统计量：将样本均数x-和样本标准差s作为总体参数μ和σ的近似值
    • 2、建立检验假设，确定检验水准
    • 3、计算检验统计量
      • （1）假设X=（X1，X2，……，Xn）是来自总体的一个随机抽取的样本
      • （2）计算全距R，确定拟分组数。组数（k）对的多少直接与卡方统计量有关，即不同分组数拟合的结果有所不同，一般要求各组理论频数不低于5。同时，自由度v与组数k有关，分组越多，自由度则越大，同一检验水准所对应的临界值也越大；且在同一自由度下，卡方值越大，对应的概率P值将越小，越有理由拒绝H0，接受H1.
      • （3）计算样本观测值落在各组段的实际频数
      • （4）计算样本值落在第i组段的概率
      • （5）计算各组对应的理论频数
      • （6）计算卡方值
        • 自由度v=k（组段数）-s（样本统计量代替总体参数的个数）-1
    • 4、确定P值，作出推断
  • 应用条件
    • 要求足够的样本含量。若样本量不够大（如：频数表有1/5以上组的理论频数1＜T＜5），可以通过连续性校正进行统计量的估算。
    • 如样本量仍然很小，可人为进行适当的合并
• Fisher确切概率法
  • 原理
    • 一种基于超几何分布理论可直接计算概率的检验方法
    • 不属于卡方检验范畴，但可作为卡方检验应用上的有益补充
    • 基本思想：保持周边合计数不变，计算交叉表中各个实际频数变动所有可能组合多对应的概率，再将获得的现有样本的概率以及比它更极端的所有概率求和，直接求出单侧或双侧的累积概率进行推断
  • 适用条件
    • 任一情况
    • 当样本含量较小时
    • 样本量n＜40
    • 有一个格子的理论数T＜1
    • 卡方检验所得概率P接近检验水准α
  • 2×2交叉表的确切概率法
    • 1、建立检验假设，确定检验水准 H0： H1： α=0.05
    • 2、计算所有可能组合的概率Pi
      • 各种可能组合的概率计算公式
      • 组合的概率Pi服从超几何分布，且∑Pi=1
        • 是单峰分布
        • 当a在合计值一半附近时对应的概率最大
    • 3、将现有样本的概率以及比它更极端的所有概率求和，直接求出单侧或双侧的累积概率，作出推断
    • 注意
      • 找出概率小或等于原四格表概率的所有四个表，将其对应的概率相加，得到双侧概率
      • 如果是单侧检验，确定P值的方法与双侧检验不同。
        • 当H1为π1＜π2时，P值为原四格表及以上的四格表的Pi之和
        • 当H1为π1＞π2时，P值为原四格表及以下的四格表的Pi之和
      • 有时可先计算当前四格表所对应的概率，若该概率已经能与检验水准作出大小比较（如已大于0.05），可直接下结论，即直接得到两组差别无统计学意义
  • R×C交叉表的确切概率法
    • 适用条件：多个样本率或多个频率的分布比较卡方检验中，一般要求其理论频数不能过小，不能有1/5以上的格子理论频数1＜T＜5，也不允许有一个格子的理论频数T＜1，否则结果容易产生偏性，此时用Fisher确切概率法
    • 一般通过软件计算实现