导图社区 人卫第8班《卫生统计学》——第十一章《直线相关与回归推断》
- 142
- 7
- 0
- 举报
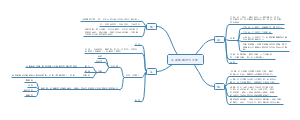
人卫第8班《卫生统计学》——第十一章《直线相关与回归推断》
人卫第8班《卫生统计学》,直线相关与回归是接下来第十三章的多重线性回归的基础,要认真学习哦~
编辑于2023-03-03 10:49:37 广东人卫第8班《卫生统计学》——第十一章《直线相关与回归推断》
社区模板帮助中心,点此进入>>
- 相似推荐
- 大纲
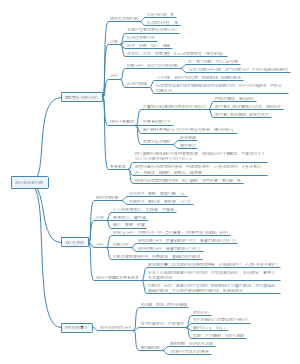
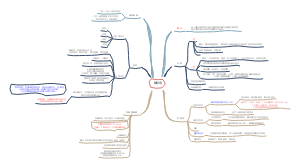
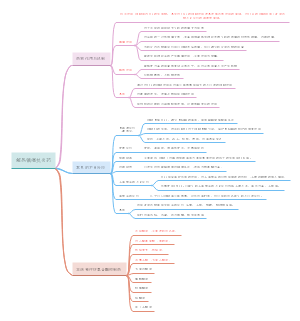
第十一章 直线相关与回归推断
概述
前后联系
联系第二章:我们学习了运用散点图、相关系数、回归系数以及回归直线等方法刻画两个变量之间的关联性
这是基于样本数据进行的描述和分析
与其他统计量类似,样本相关系数是总体相关系数的一个估计值,回归系数也是如此,本章将学习直线相关与直线回归的基本统计推断方法
本章是置信区间估计与假设检验在相关与回归中的综合应用
本章逻辑
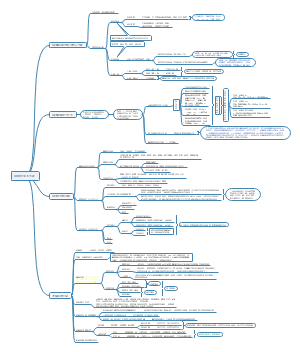
直线相关与回归推断
总体相关系数ρ
样本相关系数r
置信区间估计
假设检验
ρ=0的t检验
应用条件:两变量二元正态
总体回归系数β1
样本回归系数b1
置信区间估计
假设检验
β1=0的t检验
β1的方差分析
应用条件
直线关系
独立
正态(y)
方差齐(y)
两个或两个以上变量之间的关系强度:相关<回归
故应进行相关分析,再进行回归分析
直线相关系数的统计推断
两变量间有无直线相关关系
直线相关系数的置信区间估计
总体相关系数ρ
1、直线相关系数表示了两个变量之间直线关系的强度和方向,两变量无需区分解释变量与反应变量
2、实际工作中,常用样本相关系数r估计总体相关系数ρ
置信区间估计
1、一般情况下(ρ≠0)时,r的抽样分布并不对称,无法利用正态分布理论对ρ进行统计推断
2、利用数理理论和蒙特卡罗模拟显示,按下式对r作变换后的zr具有近似正态性:
r的取值范围为(-1,1),开区间
zr是单调增函数
3、服从均数为,标准差为的正态分布
4、故的1-α置信区间计算公式如下:
5、则总体相关系数的ρ的1-α置信区间:
直线相关系数的假设检验
ρ=0的假设检验
概述
1、样本相关系数不等于0并不表示总体中两变量一定存在直线关系
2、从相关系数为0的总体中随机抽样得到的一组样本,由于抽样误差的存在,计算得到的样本相关系数r=0.562,并不等于0
另外样本量对r的影响是十分大的
3、因此需对总体相关系数ρ是否为0进行假设检验
查表法
根据自由度v=n-2,查r界值表,比较统计量|r|与界值,统计量绝对值越大,P值越小
双侧界值
t检验
t统计量为:
双侧界值
Sr为样本相关系数r的标准误:
H0(两变量间的直线相关性无统计学意义或两变量之间无直线相关关系)成立时,tr服从自由度为v=n-2的t分布
应用到中心极限定理,样本量相对比较大的时候都服从近似正态分布,只不过要考虑到样本量的影响,所以我们用t分布
注意:假设检验只能定性地判断总体相关系数是否不为0,不代表r越大(P越小)相关性越强
应用条件
两个变量服从二元正态分布
1、如原始数据并不服从正态分布,或者属于等级资料,可以考虑秩相关系数描述相关性。
第二章
2、总体秩相关系数ρs的假设检验可以用以下方式进行推断
(1)当n≤50时,可查秩相关系数界值表,当|rs|超过界值,则拒绝H0
(2)n>50时,可采用t检验
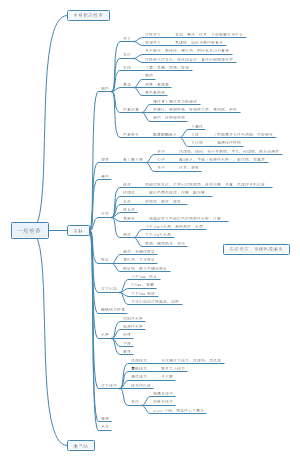
直线回归的统计推断
两变量之间有无直线回归关系
直线回归模型与参数检验
背景前提
回归方程相当于回归方模型的一次抽样获得的结果
回归模型前提条件:x固定时,y服从正态分布
因为已经确定了解释变量和反应变量,我们更关心解释变量对反应变量的影响,即y值得变化
回归模型与参数解释
1、简单直线回归模型假设y的观测值服从一系列随解释变量x变化的正态分布,其连续变化的均值取决于x值。
2、在总体回归直线中,当解释变量x的值固定时,反应变量y服从均数为的正态分布。总体回归直线如下:
表示X取某个数值时所对应的y的条件总体均数,随着x取值的变化而变化。
为总体回归直线的截距或常数项,表示x等于零0时,y的平均值。
为总体回归直线的斜率或回归系数,表示x改变一个单位时,y的平均改变量。
3、在直线回归中,假设每一个x组对应的都在回归直线上,但是由于个体观测值不一定总等于其均数。故而y的个体值与其总体均数之间有如下关系:
式中,为残差,
这里的写成σ²而不写成σyi²是因为,进行回归分析的条件之一是他们的方差齐
4、下图为总体直线回归模型示意图。直线描述了条件总体均数随着x取值的变化而变化。4个正态分布曲线反映了反应变量y随着解释变量x的4个不同取值而有所不同。
回归模型关注的是是否能够准确地预估xi条件下的y的均数
联系前面所学:对应样本的均数的相关性是比单个样本的相关性是更强的
β1的置信区间估计和假设检验
概述
1、基础:第二章第四节,基于样本数据,利用最小二乘法拟合回归直线来描述反应变量和解释变量之间的关系。
2、以此对总体回归直线的参数进行估计。在样本回归直线上,y的预测值通常用表示:
3、类似单变量分析中常需用样本均数对总体均数进行推断,在得到样本回归方程后,我们也需要推断相应总体中这种回归关系是否确实存在,即推断y的条件总体均数是否随x的变化而呈线性变化。
4、如同其他统计量,样本回归系数不等于0并不一定表示总体中两变量一定存在回归关系。
β1的置信区间
1、在第二章中,我们知道回归直线斜率的计算公式为。其中,r是y与x的相关系数,Sy为y的标准差,Sx为x的标准差。
b和r的符号一致,且ρ是否为0的假设检验和β1是否为0的假设检验结论是一致的,即tr=tb(t统计量值)
2、代数运算可验证,的计算公式也可用下式表达:
和分别表示x的离均差平方和、x与y的离均差积和。
3、是总体回归系数的一个点估计。类似于总体均数的置信区间估计,的双侧1-α置信区间:
样本回归系数的标准误与残差均方的算术平方根成正比
4、其中
是自由度v=n-2的双侧t界值
为样本回归系数b1的标准误
为残差的标准误,他是扣除x对y的影响后y的变异程度,y对于回归直线的离散程度
Sy·x度量了实际散点远离回归直线的离散程度,反映了模型的可靠性,越小模型越好
β1假设检验
β1=0的t检验
通过前述回归系数的概念可知,β1是一个“平均变化”,即自变量变化一个单位时,y的相应两个条件总体均数之差,是一个均数的概念。故对β1是否不为0的假设检验,可以将b1视为一个均数进行t检验来判断:
关注其自由度
结论:当拒绝H0时,回归方程有统计学意义
回归系数的方差分析
1、对总体回归系数的假设检验也可以利用与前述组间总体均数比较的方差分析思想来解决。
2、下图给出了两均数比较的分布示意图。
若也用回归来描述,横坐标的分组变量x取值假设为1和2。结果变量的总体均数表示为μ,两组均数分别表示为μ1和μ2。不难看出,此时两组结果变量均数之差恰好就是回归方程中的参数β1,对于β1是否不为0方差分析恰好就是两组均数是否不等的假设检验。
μ2-μ1=β1(x2-x1),则β1是否为0=(μ2-μ1)是否为0
完全随机设计的数据是可以和直线回归对应起来的,不同的处理组相当于不同的x,不同处理组对应的观测值相当于不同处理组下y的分布。基本要求也是也要的,要求y相互独立、正态、方差齐
3、由此可见,均数比较问题和回归问题都是基于条件均数的分布,回归中的个体观测值独立性、方差齐性、条件均数的线性假设和均数比较问题是一致的,对离均差平方和与自由度的分解也是相同的,只是具体操作和计算有所不同。
4、理解回归系数假设检验中方差分析的基本思想,需要分解反应变量y的离均差平方和与自由度。如下图:
5、方差分析
(1)在图中,任意一点a(x,y)的纵坐标被回归直线与均数截成三段,其。由于点a是散点图中任取的一点,若将全部数据点都按上法处理,并将等式两端平方后再求和(可以证明,下式等号右端两项中括号部分的乘积和等于0),则有:
(2)上式也可以表示为: 
称为总离均差平方。既不考虑y与x的回归关系时y的总变异。
称为回归平方。在中,由于无论回归关系如何,特定样本的均数不变,故此部分变异是由于的不同造成的,而不同正是由于两变量的回归关系引起的。因此反映了在y的总变异中可以用y与x的回归关系所解释的部分,也即y的总变异中由于y与x的回归关系而使y的总变异减少的部分。越大,说明回归效果越好。
即我们可以用回归方程预测的
称为残差平方和。他反映了除x对y的回归关系影响之外的所有一切因素对y的变异的作用,也即在总平方和中无法用回归关系解释的部分,表示考虑回归关系之后y的变异。在散点图中,各实测点离回归直线越近,越小,说明直线回归的拟合越好
(3)与组间均数比较的方差分析进行对比可见,在对反应变量的平方和分解中,回归只是用条件均数代替了均数比较中各组的组均数,而这两者的意义都是条件均数,故而在思想上两者平方和的分解是一样的。
(4)回归中上述3个离均差平方和相应的自由度之间的关系为: 
与组间均数比较的方差分析对比,两个检验的总自由度都是n-1(y的自由取值个数n减去这1个参数个数)
回归的自由度是其平方和中所含参数个数的差值决定的。对应其中前一项所含的β0和β1,减去对应后一项中一个参数,所以自由度为1
残差自由度因其平方和中暗含β0和β1两个参数,故其自由度为n-2
(5)由离均差平方和及其自由度的分解可见,当β1接近于0时,更可能出现较小的和较大的;而当β1远离0时,更可能得到较大的和较小的。故相对于随机误差而言,回归所解释的变异越大,越有理由认为β1≠0.
(6)或者可认为不考虑回归时,随机误差是y的总变异,而考虑回归后,扣除回归的贡献使随机误差减小为。如果两变量间总体回归关系确实存在,回归的贡献应大于随机误差,大到何种程度时可以认为具有统计学意义,可根据和的关系构造F统计量:
其中:MS为均方,在H0:β1=0的假设下,统计量F服从v回,v残的F分布
(7)实际计算时,可以利用下式直接求得。
b1代表y的变异
lxx代表的是x的总变异
(8)在直线回归中,对同一数据做总体回归系数β1是否不为0 的假设检验,方差分析和t检验是一致的:
它们有相同的自由度、应用条件
当v=1时
假设检验结论:当拒绝H0时,回归方程有统计学意义,可以认为两变量间有直线回归关系
直线回归分析的应用
反应变量平均值的置信区间
回归直线的置信带
1、给定数值,由样本回归方程算出的只是条件总体均数的一个点估计值。由于存在抽样误差,会因样本而异,反映其抽样误差大小的标准误可按下式计算:
x确定时
2、其条件总体均数的双侧(1-α)置信区间的计算公式为:
注意自由度
3、用同样的方式,可计算出所有x对应y的总体均数95%置信区间。以x为横坐标,y为纵坐标,将自信期间的上下限分别连起来形成两条弧线间的区域,称为回归直线的置信带。
4、两条性质
当,反应变量总体均数的标准误达到最小值,其对应的置信带最窄。离越远,其标准误越大,对应的置信带越宽。
样本量越大,对应的反应变量总体均数的标准误也越小,置信区间带越窄
反应变量个体值的预测区间
1、利用回归方程进行统计预测,就是将解释变量带入回归方程中,对反应变量的个体值进行估计。给定数值对应的个体y也存在一个波动范围,其标准差可按下式计算:
与置信区间的不同在于标准误的不同
置信区间
均值的标准误
个体观测值的预测区间
残差的标准误+均值的标准误
样本量对其影响比较小,且变异比较小,两条线接近于平行
2、因此,时个体y值得双侧(1-α)预测区间为:
3、值得注意的是,当时,其条件总体均数的置信区间与个体y值的预测区间含义是不同的:
前者表示在固定的处,反复抽样100次,可算出100个相应y的总体均数的置信区间,在概率意义上平均而言,有100×(1-α)个置信区间包含总体均数;
总体均数是否在这个范围之内→对应置信区间的概念
而后者表示个体值的取值范围,即在固定的处,随机抽取100个个体。平均有100×(1-α)个个体值在求出的范围内。(对应正态分布的应用——可以提供参考值范围)
当x=xp时对应的y的参考值范围→对应医学参考值的范围
4、用同样的方法,可计算出所有x值对应的y值的95%预测区间,以x为横坐标,y为纵坐标,将预测区间的上下限分别连起来形成的两条弧形线间的区域,称为y的预测带。
5、同一x值下,个体y值得预测区间要宽于条件平均值的可信区间
应用条件
概述
1、类似于单变量情形。在小样本时,直线回归涉及的统计推断问题都基于F分布。
2、统计模型是基于一系列假设条件下对客观现象的抽象化表示,独立、正态分布、方差齐的若干解释变量的条件均数恰好在一条直线上要是直线回归模型的基本假设。实际数据是否满足这些假设可以用统计学方法进行判断。但较为简单直观的方法是观察原始数据散点图和各种残差图。
3、如果实际数据在不满足应用条件的情况下进行直线回归分析,将影响回归系数估计的精度与假设检验的P值,甚至可能得到专业上无法解释的结论。
条件
反应变量与解释变量之间呈直线关系
各观测值相互独立
解释变量固定时所对应反应变量服从条件正态分布
不同解释变量取之下反应变量的条件方差相等,即方差齐。
方差分析的应用条件