导图社区 第四章 工程计价方法与依据
- 171
- 6
- 2
- 举报
第四章 工程计价方法与依据
建设工程造价管理第四章 工程计价方法与依据基础知识总结,包括工程计价方法、工程计价依据的分类,人工、材料、机具台班消耗量定额等。
编辑于2022-03-27 15:18:08- 建设工程造价管理
- 全国二级…
- 工程计价方法与依据
- 相似推荐
- 大纲
第四章 工程计价方法与依据
工程计价方法
工程计价的基本方法
工程计价顺序
分部分项工程计价
单位工程计价
单项工程计价
建设工程总造价
工程计价
工程定额计价
工程定额主要用于国有资金投资工程编制投资估算、设计概算、施工图预算
对非国有资金投资工程,在项目建设前期和交易阶段,作为计价的辅助依据
工程量清单计价
工程量清单主要用于建设工程发承包及实施阶段
工程量清单计价用于合同价格形成以及后续的合同价款管理
综合单价
是完成工程量清单中一个规定计量单位项目所需的人工费、材料费、施工机具使用费、管理费、利润、一定范围的风险费用
工程定额计价
工程定额的原理和作用
原理
工程定额是指在正常施工条件下完成规定计量单位的合格建筑安装工程所消耗的人工、材料、施工机具台班、工期天数及相关费率等的数量标准(费用标准)
分类
按不同用途
施工定额(企业性质)
预算定额
概算定额
概算指标
估算指标
按不同的编制单位和执行范围
全国统一定额
行业定额
地区统一定额
企业定额
补充定额
作用
施工定额
施工定额是指完成一定计量单位的某一施工过程,或基本工序所需消耗的人工、材料和施工机具台班数量标准
施工定额是施工企业成本管理和工料分析的重要依据
预算定额
预算定额是在正常的施工条件下,完成一定计量单位合格分项工程和结构构件所需消耗的人工、材料、施工机具台班数量及其费用标准
预算定额是一种计价性定额,以施工定额为基础综合扩大编制而成
主要用于施工图预算的编制,也可用于工程量清单计价中的综合单价的计算
概算定额
概算定额是完成单位合格扩大分项工程,或扩大结构构件所需消耗的人工、材料、施工机具台班的数量及其费用标准
概算定额是一种计价定额,基本反映完成扩大分项工程的人材机消耗量及其相应费用,以预算定额为基础综合扩大编制而成
主要用于设计概算的编制
概算指标
概算招标是以扩大分项工程为对象,反映完成规定计量单位的建筑安装工程资源消耗的经济指标
概算指标是一种计价定额,主要用于编制初步设计概算
投资估算指标
投资估算指标是以建设项目、单项工程、单位工程为对象,反映其建设总投资及其各项费用构成的经济指标
投资估算指标是一种计价定额,主要用于编制投资估算
包括建设项目综合估算指标、单项工程估算指标、单位工程估算指标
工程定额计价的程序⑧
收集资料
熟悉图纸和现场
计算定额工程量(考虑一定施工方法)
套定额单价
编制工料分析表
费用计算
复核
编制说明
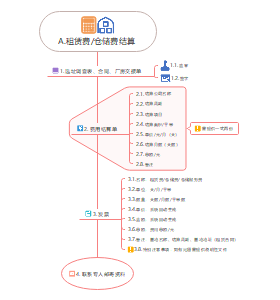
工程量清单计价
工程量清单的原理和作用
原理:根据清单规范规定列清单项目,计算清单项目工程量,根据规定的方法计算出综合单价,汇总各清单合价得出工程总价
范围
工程量清单计价活动涵盖施工招标、合同管理、竣工交付全过程
主要包括编制招标工程量清单、最高投标限价、投标报价,确定合同价,工程计量与价款支付、合同价款的调整、工程结算和工程计价纠纷处理等活动
作用
提供一个平等的竞争条件
满足市场经济条件下竞争的需要
有利于工程款的拨付和工程造价的最终结算
有利于招标人对投资的控制
工程量清单计价的程序⑧
收集资料
熟悉图纸和现场
计算清单工程量(不考虑一定施工方法,净量)
工程量项目组价
形成综合单价分析表
费用计算
分部分项工程费=∑(分部分项工程量×分部分项工程项目综合单价)
单价措施项目费=∑(措施项目工程量×措施项目综合单价)
总价措施项目费=∑(措施项目费计费基数×费率)
单位工程造价=分部分项工程费+措施项目费+其他项目费+规费+增值税
复核
编制说明
工程计价依据的分类
工程计价依据体系
法律法规:XX法、XX条例、XX适用法律问题的解释
部门规章:XX规定、XX办法
国家标准:XX规范
全国统一定额:XX定额
协会标准:XX规程
工程计价依据的分类
按用途分类 (7大类、20小类)
规范工程计价的依据
国家标准
有关行业主管部门发布的规章、规范
行业协会推荐性规程
计算设备数量和工程量的依据
可行性研究资料
初步设计、扩大初步设计、施工图设计图纸和资料
工程变更及现场签证
计算分部分项工程人工、材料、机具台班消耗量及费用的依据
概算指标、概算定额、预算定额
人工单价
材料预算单价
机具台班单价
工程造价信息
计算建筑安装工程费用的依据
费用定额
价格指数
计算设备费的依据
设备价格、运杂费率
计算工程建设其他费用的依据
用地指标
各项工程其他费用
相关的法规和政策
包含在工程造价内的税种、税率
与产业政策、能源政策、环境政策和土地等资源利用政策有关的取费标准
利率、汇率
其他
按使用对象分类(单位)
规范建设单位计价行为的依据
可行性研究
用地指标
工程建设其他费用定额
规范建设单位和承包商双方计价行为的依据
预算定额、概算定额、 概算指标、投资估算指标和造价指标
预算定额
作用
是编制施工图预算、确定建筑安装工程造价的基础
是编制施工组织设计的依据
是施工单位进行经济活动分析的依据
是编制概算定额的基础
是合理编制最高投标限价的基础
编制原则
社会平均水平原则
简明适用原则
编制依据
现行施工定额
现行设计规范、施工及验收规范,质量评定标准和安全操作规程
具有代表性的典型工程施工图及有关标准图
新技术、新结构、新材料和先进的施工方法
有关科学实验、技术测定和统计、经验资料
现行的预算定额、材料单价及有关文件规定
消耗量的确定
计量单位的确定
人、材、机消耗量的确定
人工消耗量
基本用工 (施工定额)
完成定额计量单位的主要用工
超运距用工
平均运距比劳动定额中的平均运距远
辅助用工
现场加工材料用工:筛砂子、淋石灰膏
人工幅度差
正常施工条件下,劳动定额中没有包含的用工因素
例如:各工种交叉作业配合工作的停歇时间, 工程质量检查和工程隐蔽、验收等所占用的时间
材料消耗量
材料
主要材料
直接构成工程实体的材料(钢筋、水泥)
辅助材料
构成实体主要材料外的其他材料(垫木、钉子、铅丝)
周转性材料
脚手架、模板多次周转使用,但不构成工程实体的摊销材料
其他材料
难以计量的零星用料(棉纱、编号用的油漆)
凡设计图纸标注尺寸及下料要求的,按设计图纸计算材料净用量(砼、钢筋)
材料损耗量是在正常施工条件下,不可避免的材料损耗,按经验确定(现场内材料运输损耗、操作过程中的损耗;现场外材料运输损耗算在材料单价)
周转性材料按材料使用次数及损耗率确定
机具台班消耗量
以使用机械为主的项目,如机械挖土、空心板吊装等,要相应增加机械幅度差(占有工作面)
施工机具是配合工人班组工作的,如砌墙是按工人小组配置塔吊、卷扬机、砂浆搅拌机,不增加机械幅度差
概算定额
主要作用
编制设计概算和修正概算
对项目设计进行技术经济分析和比较的基础
编制主要材料计划的参考依据
编制概算指标的依据
编制依据
现行预算定额
设计及施工技术规范
典型工程施工图和其他材料
人工工资标准、材料预算价格、机械台班预算价格
概算指标
主要作用
编制投资估算、编制基本建设计划、估算主要材料用量计划的依据
编制初设概算、选择设计方案的依据
考核基本建设投资效果
编制依据
标准设计图纸、各类工程典型设计
国家标准、规范
各类工程造价资料
概算定额、预算定额及补充定额
人工工资标准、材料预算价格、机械台班预算价格
投资估算指标
内容 (三个层次)
建设项目综合指标
包括单项工程投资(工程费用)、工程建设其他费用、预备费
单项工程指标
包括建筑工程费、安装工程费、设备、、工具及生产家具购置费(工程费用)
单位工程指标
建筑安装工程费(能独立设计、施工的工程项目的费用)
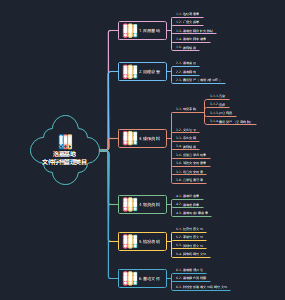
人工、材料、机具台班消耗量定额
人工、材料、机具台班消耗量以劳动定额、材料消耗量定额、机具台班消耗量定额的形式来表现,是工程计价最基础的定额, 是地方和行业部门编制预算定额的基础, 是个别企业依据其自身的消耗水平编制企业定额的基础
劳动定额
分类及关系
时间定额:指在某工种某一等级的工人或工人小组在合理的劳动组织等施工条件下, 完成单位合格产品所必须消耗的工作时间
产量定额:是指某工种某等级工人或工人小组在合理的劳动组织等施工条件下, 在单位时间内完成合格产品的数量
工作时间
工作时间是指工作班的延续时间 建筑安装企业工作班的延续时间为8h(每个工日)
工作时间消耗的研究 分为两个系统
工人工作时间
必须消耗的时间
有效工作时间
基本工作时间
内容:与产品生产直接有关,一般与工作量大小成正比
例如:砌砖中挂线、铺灰浆
辅助工作时间
内容:同技术操作无直接关系的辅助性工作时间
例如:修磨检验工具、移动工作梯、工人转移工作地点
准备与结束工作时间
内容:执行任务前准备,完成任务后整理
休息时间
内容:工人恢复体力所必需的时间
不可避免的中断时间
内容:施工工艺特点所引起的工作中断时间
例如:汽车司机等候装货、安装工人等候构件起吊
损失时间
损失时间是与产品生产无关,而与施工组织和技术上的缺点有关,与工人在施工过程中的个人过失或某些偶然因素有关的时间消耗
多余和偶然工作时间
内容:正常施工条件下不应发生的时间消耗
例如:拆除超过图示高度的多余墙体的时间
停工时间
内容:施工本身造成的停工时间和非施工本身造成的停工时间
例如:材料供应不及时,由于气候变化和水、电源中断而引起的停工时间
违反劳动纪律的损失时间
例如:在工作班内工人迟到、早退、闲谈、办私事
工人所使用的机器工作时间 (机械工作时间)
必须消耗的时间
有效工作时间
正常负荷下的工作时间
有根据的降低负荷下的工作时间
不可避免的无负荷工作时间
内容:由施工过程的特点所造成的无负荷工作时间
例如:推土机到达工作段终端后倒车时间, 起重机吊完构件后返回构件堆放地点的时间
不可避免的中断时间
内容:与工艺过程的特点、机械使用中的保养、工人休息等有关的中断时间
例如:汽车装卸货物的停车时间,给机械加油时间,工人休息时的停机时间
损失时间
机械多余的工作时间
内容:完成任务时无须包括的工作占用时间
例如:灰浆搅拌机多运转时间,工人没有及时供料的机器空转
机械停工时间
内容:由于施工组织不好及由于气候条件影响所引起的停工时间
例如:未能及时给机械加水、加油
违反劳动纪律的停工时间
内容:工人迟到早退引起的机械停工时间
例如:在工作班内工人迟到、早退、闲谈、办私事
低负荷下工作时间
内容:工人或技术人员的过错所造成的施工机具在降低负荷的情况下工作的时间
编制方法
经验估计法
特点:方法简单、工作量小,定额准确性差
适用:多品种生产或单件、小批量生产的企业,新产品试制、临时性生产
统计分析法
根据过去生产同类型产品、零件的实作时间/统计资料,整理分析
适用:大量生产或成批生产的企业,生产条件比较正常、产品较固定、原始记录和统计工作较健全的企业
技术测定法
优点:准确性较好
缺点:费时费力,工作量较大
比较类推法 (典型定额法)
具备条件:结构相似、工艺同类、条件可比、变化规律
优点:准确性和平衡性较好
缺点:工作量较大
材料消耗定额
材料消耗定额包括 (不含现场外运输损耗)
直接用于建筑安装工程的材料
不可避免的施工废料
不可避免的施工操作损耗
净用量定额与 损耗量定额的关系
总消耗量=净用量+损耗量=净用量×(1+损耗率)
编制材料消耗定额 的基本方法
现场技术测定法
一般材料的净用量比较容易确定,损耗量不能随意确定,需通过技术测定区分难以避免的损耗及可以避免的损耗,从而确定出较准确的材料损耗量
实验室试验法
精确度高,易脱离现场实际情况
统计法
通过对现场用料的大量统计资料进行分析
理论计算法
运用计算公式计算材料消耗量,适合计算块状、板状、卷状等材料的消耗量
砖砌体材料净用量
标准砖尺寸:240mm×115mm×53mm
砂浆用量:B=1-砖数×砖块体积
各种块料面层的材料净用量
施工机具台班定额
人工、材料、机具台班单价及定额基价
人工单价
人工日工资单价组成 (不含加班加点工资)
计时工资/计件工资
奖金
津贴补贴
特殊情况下支付的工资
人工日工资单价确定方法
年平均每月法定节假日
日工资单价计算
日工资单价管理
人工日工资单价在我国具有一定的政策性, 最低日工资单价≥工程所在地最低工资标准
普工1.3倍 一般技工2倍 高级技工3倍
材料单价
组成
材料原价
材料运杂费
运输损耗费
采购及保险费
各项费用的确定
运输损耗费
材料在运输和装卸过程中不可避免的损耗(施工现场外)
材料运输损耗=(材料原价+材料运杂费)×运输损耗率
采购及保管费
组成
采购费
仓储费
工地保管费
仓储损耗
采购及保管费=(材料原价+材料运杂费+运输损耗费)×采购及保管费费率
材料单价=【(材料原价+材料运杂费)×(1+运输损耗率)】×(1+采购及保管费费率)
一般计税方法,材料原价、运杂费均应扣除增值税进项税额
施工机具台班单价
施工机械台班单价组成(7) 安旧动工检维其
折旧费
检修费
维护费
安拆费及场外运费
人工费
燃料动力费
其他费用
施工仪器仪表台班单价(4) 动折护校
折旧费
维护费
校验费
动力费
定额基价
概念:指反映完成定额项目规定的单位建筑安装产品,在定额编制基期所需的人工费、材料费、施工机具使用费或其总和
构成
定额项目基价=人工费+材料费+施工机具使用费
人工费=定额项目工日数×人工单价
材料费=∑(定额项目材料用量×材料单价)
施工机具费=∑(定额项目台班量×台班单价)
套用
换算
类型
当设计要求与定额项目配合比、材料不同时的换算
乘以系数的换算
基本思路
换算后定额基价=原定额基价+换入费用-换出费用
适用范围
砂浆强度等级
混凝土强度等级
抹灰砂浆
其他配合比材料
建筑安装工程费用定额
编制原则
合理确定定额水平的原则
简明、适用性原则
定性与定量分析相结合的原则
企业管理费和规费费率的确定
计算基数
直接费(人材机)
人工费+施工机具使用费
人工费
利润
计算公式:利润=取费基数×相应利润率
基数
人工费
直接费
直接费+间接费
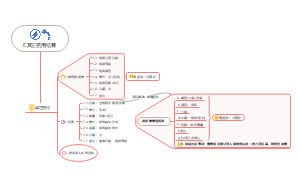
工程造价信息及应用
工程造价信息 概念和特点
工程造价指数
概念和意义
概念:工程造价指数是一定时期的建设工程造价相对于某一固定时期工程造价的比值,以某一设定值为参照得出的同比例数值。用来反映一定时期由于价格变化对工程造价的影响程度,是调整工程造价价差的依据,反映了报告期与基数相比的价格变动趋势
意义
可分析价格变动趋势及其原因
可预计宏观经济变化对工程造价的影响
是工程发承包双方进行工程估价和结算的重要依据
内容及其特征
各种单项价格指数
内容:人工费、材料费、施工机具使用费、各种费率指数
特点:个体指数
设备、工器具价格指数
内容:由不同规格、不同品种设备工器具组成
特点:总指数→综合指数
建筑安装工程造价指数
内容:各项个体指数的影响,各项的加权平均
特点:总指数→平均指数
建设项目或单项工程造价指数
内容:各种指数平均
特点:总指数→平均指数
工程造价信息 的动态管理
信息技术在工程造价 计价与计量中的应用
BIM技术与工程造价
BIM技术特点
可视化
协调性
模拟性
互用性
优化性
在工程造价管理 各阶段的应用
决策阶段
高效准确估算出规划项目的总投资额
设计阶段
设计方案优选或限额设计,多专业一致检查
招投标阶段
工程量自动计算、统计分析,形成准确的工程量清单
施工过程
直观看到项目具体实施情况并得到该节点的造价数据
工程竣工结算
提高工程量计算的效率和准确性