衍生4-forward rate and fras

这是一篇关于衍生4-forward rate and fras的金融学思维导图。

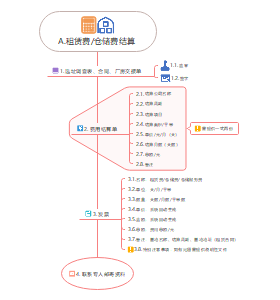
4-forward rate and fras

• rates & value
  • bond value (计算债券的现值)
    • 关键信息
      • 
      • time to maturity
      • face value/principal
        • the money u will receive at the maturity
      • coupon rate
        • 所标的利率是年化的
      • payment frequency
        • 会影响coupon rate,以致coupon payment
      • bond yield
        • discount rate of cash flow
  • zero rate/spot rate(零息利率)
    • 概念：provide a payoff only at time T (不考虑息票率的收益率)
    • 公式：
    • 计算1： determine treasury zero rate ——bootstrap method (票息剥离方法)
      • 原理： 将息票从债券中剥离出来并以此进行zero rate计算的方法
      • 计算
        • 小于等于一年： 1/T*In(FV/bond price)
          • 
        • 大于一年： 设置该年的zero rate为R，用不同时期的zero rate立公式， 解方程得到该年zero rate
          • 
    • 计算2： use zero rate to calculate bond pricing
      • 原理：discount rate for different time varies, so we should discount each cash flow at proper zero rate
      • 例题：
  • bond yield (债券收益率)
    • 概念： the discount rate that makes the present value of cash flow equal to the market price of the bond
    • 公式：
    • 计算器计算： 先算复利 (不是年化利率，而是对应发coupon的利率， 所以N和PMT都是算细分的) 然后再转化为连续复利 Rcc = frequency*ln(1+isa)
  • par yield (平价收益率)
    • 概念： the coupon rate that causes the bond price equal to face value
    • 公式：
      • 这里的c虽然只是一个利率，但是去掉了%， 所以相当于‘*100’
    • 计算： d是总共时长的贴现值 A是不同时期贴现值的相加
  • 当PV = FV时，bond yield = par yield
    • 平价债券率就是发行价格等于面值，而YTM就是所有现金流的贴现率。 当贴现出来的价格等于面值时，两者是相等的 （记住就行，原因不做说明）
• forward rates
  • 概念： the future zero rate implies by today's term structure of interest rates
    • 解释： 远期利率是受即期利率所影响的 
    • 注意远期利率是对于未来利率的一种预测。 时间越接近未来预期点，forward rate will converge to the actual rate （forward rate 每天都要调整变化的）
  • 计算
    • 原理： 在市场中，假设有两种方案可以选择，一个是直接用即期利率进行投资 一个是一年用即期，一年用远期 而这两种方案的收益应该是同样的（否则将被市场淘汰）
    • T1,T2/R1,R2分别是1，2年的数据
      • 
      • 如果不用连续复利：
      • 注意：算的远期利率应该是T2的利率
  • instantaneous forward rate (瞬态远期利率)
    • 概念： the forward rate that applies for a very short period
    • 公式： R是即期利率
      • 关系变化： 如果斜率upward sloping,Rf>R,反之亦成立
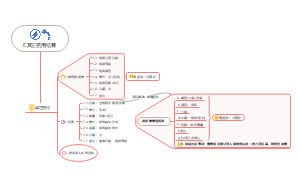
• forward rate agreement (FRA——远期利率合约)
  • 概念： 一种利率合同 双方双方针对特定货币和期限的一笔名义存款或贷款 约定利率水平 并在结算日根据市场实际利率水平结算利息差额 (normally be LIBOR)
  • 参与方： long position would borrow the money (贷款方)
    • if LOBOR rate > stipulated rate, long earns positive money
  • payoff
    • 基本信息
      • forward price K: the forward rate of the underlying asset
      • underlying asset:floating rate(eg.LOBOR)
      • contract value: the principal L
    • 时间线
      • FRA initiation约定日： 双方签下FRA合同，约定在未来某一天开始交易
      • FRA expiration起息日
        • 有点像对冲策略 long borrows L from the short position at K long lends L in the spot market at K
      • loan maturity 到期日： close positions and calculate the net interest difference
    • so
      • for long position:
        • 帮助理解一下： 用K买入的，那么如果现价S高了的话，说明自己是以低价买入的，是一种隐形的payoff
      • for short position:
  • cash settlement
    • 原理： 现金结算，可以提前拿到钱 因为在FRA expiration已经可以观察到St了(K是签合同的时候就知道的)
    • 基本信息
      • 
      • Rk：the contract agreed interest rate
      • Rf: the forward LIBOR rate for T1-T2 at t(T0-T1)
      • Rm: the actual LIBOR rate for T1-T2 at T1
      • Rf:risk-free rate for T0-T2 with continuous compounded
        • 要注意题给的是cc还是annually compounded,条件不同解题方法也不同
    • compounding frequency: Rf和Rk的compounding frequency correspond to the length between T1-T2
      • if T2 - T1 = 1 year,frequency is annually compounding
      • if T2 - T1 = 1 month,frequency is monthly compounding
    • pricing:settlement
      •  1year是T0-T1，6 month 是T1-T2， 现在所在的观测点就是T0
      • pricing before expiration:at t
        • t时刻对于long position's gain: Rf: the updated forward price of LIBOR
          • Rk是t=0时所设置的合同利率，此后Rf一直都是不断变化的，直到T1时刻 而计算在结算日之前的收益，就是计算Rf和Rk的差价， 前三个乘式都可以理解，就是结算日到到期日这段时间的收益 后面是要把现金流贴现到t时刻
      • pricing at expiration:at T1
    • timeline
      • number1: until the contract expires (从T0-T1)
      • number2: until the underlying loan is settled (从T0-T2)
        • eg.'2*3 FRA'，就是a 1-month loan in 2-month
      • 隐藏的的number3：the maturity of the underlying loan (从T1-T2)