衍生10-property(性质) of stock option

这是一篇关于衍生10-property(性质) of stock option的思维导图

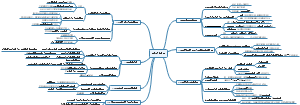
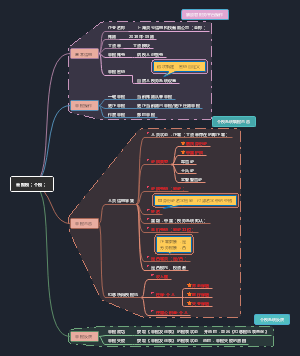
10-property(性质) of stock option

• upper & lower bounds of option price
  • American VS European: A provides more exrcise opportunity than E (only be exercise at maturity 也就是说，A可以随时交易，但E只能在到期日时交易) C ≥ c P ≥ p
    • 
  • for call
    • upper bound(上限) for European/American call option prices
      • c/C ≤ So call option can never be worth more than stock,otherwise people will buy stock directly
        • proof: if C > So. borrow So and buy one share of stock short an A call and close liability position(卖掉call期权) total profit: C-So, so there's an arbitrage opportunity since c ≤ C，we have c ≤ So
    • lower bound(下限) for European/American call option prices
      • to avoid arbitrage,there's a case
        • arbitrtage strategy T0: short-sell stock and receive So long a call option, pay c invest (So - c) T1: receive investment income (So-c)e^rT if St>K: exercise option and close the short-selling position. earning is (So-c)e^rT - K if St<K: do not exercise option,use St to buy stock to close position.earning will more than (So-c)e^rT - K
        • T0
          • short-sell one unit of stock and receive S0
          • long a call option for one unit of the stock and pay c
          • invest S0 - c for T year at rf
        • T1
          • investment income is (S0 - c)e^(rf*T)
          • strategy
            • if St > K: exercise option and close short-selling position (执行期权，买下股票，并将股票还给broker)
              • earning:
              • to avoid arbitrage:
            • if St < K: do not exercise option,use St to buy stock and close the short-selling position
              • earning:
              • to avoid arbitrage:
      • lower bound for E&A(no dividend)
        • (cuz K can be any positive number)
        • more formal argument(另一种推导理论)
          • portfolio A： E call option + zero-coupon bond with payoff K at T
            • price:
            • at T,payoff:
          • portfolio B: one share stock
            • price: S0
            • at T,payoff: St
          • cuz payoff A > B.so the price of A must be higher than B
  • for put
    • upper bound for European/American put option prices
      • for E:
        • if p ≥ Ke^(-rT),you can short the put an invest at r(卖出期权，把钱拿来投资) 而在T time,can buy the stock from long position at K  so there's an arbitrage
      • for A:P ≤ K 由于A put option allows holder to sell stock of K at any time before maturity
    • lower bound for European/American put option prices
      • to avoid arbitrage,there's a case
        • arbitrage strategy T0: borrow c+So long a put option and pay c buy stock and pay So T1: if St>K: do not exercise the option,sell the share and receive St(St>K) if St<K: exercise option,receive K clear the liability (c+So)e^rT,and net gain will be higher than K-(c+So)e^rT
        • T0
          • borrow S0+p
          • long a put option and pay p,buy stock and pay S0 (用借来的钱买看跌期权和股票)
        • T1
          • clear the liability and pay
          • strategy
            • if St > K: do not exercise the option,sell stock and receive St
              • to avoid arbitrage:
            • if St < K: sell the stock to short position and receive K
              • to avoid arbitrage:
      • lower bound for E(no dividend)
        • more formal argument
          • portfolio C: E put option + stock
            • price:
            • payoff:
          • portfolio D: zero-coupon bond payoff K at T
            • price:
            • payoff:K
          • payoff is C > D,so the price of C will be more expensive
      • lower bound for A(no dividend)
        • P > max(K-So,0)
          • cuz if P < K - So, at this time,K-So > 0 if exercise option quickly,get K,which > P+So, so it's an arbitrage
• effect of dividends
  • lower bound for E call
    • • portfolio A: call+stock price:c+D+Ke^(-rt) payoff:max(St,K)+FV(D) portfolio B: stock price:So payoff:St+FV(D)
  • lower bound for E put
  • put-call parity of E
  • put-call parity of A
• put-call parity(看跌看涨期权平价关系式)
  • put-call parity for European options
    • portfolio A: call + zero-coupon bond,price is (c+Ke^(-rt))
    • portfolio C: put + stock,price is (p+So)
    • value of portfolio
      • (c+Ke^(-rt)) = p+So value is same at the maturity, so they must be worth the same today
        • find arbitrage opportunity
          • if p > p',that is p+So > c+Ke^(-ft)
            • T0
              • short C: receive p+So
              • long A: long a call and invest (p+So)-c
            • T1
              • if St>K: exercise the call,can buy the stock at K
              • if St<K: exercise the put,can buy the stock at K
            • net gain:(p+So-c)e^(rt)-K
          • if p < p',that is p+So < c+Ke^(-ft)
            • T0
              • short A: short call and borrow
              • long C: long a put and stock,pay p+So
            • T1
              • if St>K: exercise call,sell stock at K
              • if St<K: exercise put,sell stock at K
            • net gain: K-borrowe^(rt)
  • put-call parity for American options
    • • proof: C-P ≤So-Ke^(-rT) cuz A put option is more valuable than E put option(P≥p) A call option won't exercise early(C=c) 因为可以提前行权，所以更具有价值，价格也会更高一点 so it can be concluded So-K≤C-P suppose there are two portfolios portfolio E:european call+cash K price:c+K payoff:at T,max(St-K,0)+Ke^(rT) at t,Ke^(rT) 因为E option没办法提前行权 portfolio F:american put option+one share stock price:P+So payoff:at T,max(St,K) 卖掉股票，要么是成交价，要么是现价 at t,when K≥St,is K 两种情况，E都比F价值高，so it can be concluded
• early exercise of American option (提前执行)
  • exception: a call with non-dividend paying stock
  • put option should always be exercised early if it is sufficiently deep in the money
• factors affecting option price
  • stock price(S) & strike price(K)
  • time to expiration(T)
    • for A option: long-life provides more chance,so it's more valuable
    • for E option: the relationship is uncertain
  • volatility(σ)
    • owner will benefit from this as the downside risk is limited
  • Rf(r)
    • increase expected stock return
    • decrease PV
    • effects
      • increase call price
      • decrease put price
  • amount of future dividend(d)
    • decrease P(call)
    • increase P(put)
    • 原理： reduce stock price on ex-dividend date 股价下跌，看跌期权就会涨