24一建经济第1章

本导图的主要目的旨在学习一建经济的同时，将已学到的知识点分享与大家进行参考。希望在各位前辈的指导下共同进步。

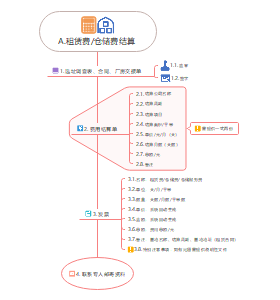
第1章资金时间价值计算及应用

• 1.1利息的计算★★★
  • 1.1.1利息和利率
    • 1.利息的含义
      • 在资金债权债务关系中，债务人（需求方）支付给债权人（供给方）的资金总额超过其最初从债权人所获资金数额的部分，称为利息。即还本付息总金额和本金之差。
    • 2.利息的本质
      • 从本质上看，利息是对资金供给方（债权人）放弃一定时期资金使用权的补偿（机会成本）；是资金供给者的报酬（收益），同时也是资金需求者使用资金的代价（成本）。
      • 来源于资金发挥运营职能而形成的利润的一部分。
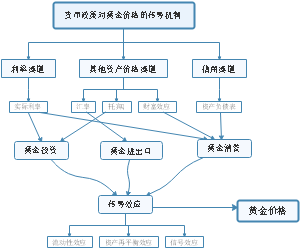
    • 3.利息对经济活动的影响
      • 对企业影响 合理利用资金，减少资金占用，提高资金周转效率；并直接影响企业资金筹措决策。 对居民影响 利息收入的高低，是居民资金使用方式决策的重要依据，从而影响其资产使用行为。 对政府影响 通过利息手段调节微观主体（企业、居民）行为，为特定宏观经济管理目的服务。
    • 4.利率
      • (1)利率的含义
        • 也称利息率，是单位时间内应得或应付利息额与本金之比，一般用百分数表示。
        • 『提示1』计息周期：计算利息的时间单位，通常为年、半年、季、月、周或日。
        • [结论1]利息是资金收益或使用代价的绝对数，利率是资金收益或使用代价的相对数，均可表示资金的增值程度。
      • (2)利率的影响因素
        • 影响因素 变动关系 社会平均利润率 最高界限 供求对比状况 供过于求，下降；供不应求：上升 资金承担的风险 正向变动 债务资金使用期限 正向变动 宏观调控政策 通过信贷政策影响市场利率 所处经济周期不同阶段 扩张期：上升；衰退期：下降。
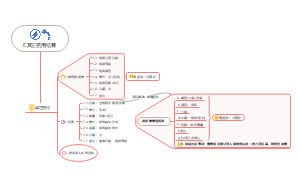
  • 1.1.2利息的计算方法
    • 1.单利计息
      • 『利不生利』
      • 『结论2』在以单利计息的情况下，如果各期利率不变，总利息与本金，利率以及计息周期数成正比关系：
      • 第t期利息：
      • 第t期期末本利和：
    • 2.复利计息
      • 『利滚利』
      • 『结论3』在计算某一计息周期的利息额时，其先前计息周期所累积的利息要作为计算本期利息的基数，即“利生利”“利滚利”的计息方式：
      • 第t期利息：
      • 第t期期末本利和：
    • 3.单利和复利的比较
      • 『结论4』在计息周期数超过1时，单利计息和复利计息就会存在差异；计息周期越多，两者差距就越大。
      • 『结论5』本金越大，利率越高，计息周期数越多，复利计息金额与单利计息金额差距越大。
      • 『结论6』在工程经济分析中，一般采用复利计息方式计算。
      • 『结论7』按期（年、半年、季、月、周、日）计算复利的方法称为间断复利（普通复利），按瞬时计算复利的方法称为连续复利。在实际使用中采用间断复利。
      • 『小结』
        • 计息方式 计息基础 计算公式 当计息期超过1期 单利计息 本金 It＝P×i单 总体利息少 复利计息 上期末本利和 It＝I×Ft-1 总体利息多
• 1.2名义利率与有效利率★★
  • 当计息周期小于一年时，就出现了名义利率和有效利率的概念。
  • 1.2.1名义利率的计算
    • 概念：计息周期利率i乘以一年内的计息周期数m所得的年利率，即：
    • 『提示2』通常公布的年利率为名义利率。
  • 1.2.2有效利率的计算
    • 计息周期有效利率  年有效利率 
    • 『结论8』计息期数越多（计息周期越短），年名义利率和有效利率的差别越大。
    • 『结论9』在工程经济分析中，如果各技术方案的计息期不同，就不能使用名义利率来评价，而必须换算成有效利率进行评价，否则会得出不正确的结论。
• 1.3资金等值计算及应用
  • 资金的价值是随时间变化而变化的，是时间的函数，随时间的推移而增值，资金的增值部分就是原有资金的时间价值。
  • 1.3.1资金时间价值的影响因素
    • 影响因素 变动关系 资金的使用时机 不同时机产生的价值有可能不同 资金的使用时长 正向变动 资金数量的多少 正向变动 资金周转的速度 正向变动
  • 1.3.2资金的等值计算
    • 不同时期、不同数额但其“价值等效”的资金称为等值，又叫等效值。
    • 1.现金流量图和现金流量表
      • 现金流量视角：特定的技术方案。
      • 现金流量的类别：
      • （1）现金流量图
        • 『结论10』四个步骤：
          • 1.时间轴；
          • 2.确定方向（注意系统角度）；
          • 3.发生时点；
          • 4.数额大小。
        • 『结论11』现金流量三要素：现金流量的大小、方向和作用点。
      • （2）现金流量表
        • 『提示3』现金流量表中，时间单位数值表示该时间单位期末，记在某一时间单位的现金流量视为发生在该期期末；
        • 『提示4』现金流量表中分列现金流入和现金流出时，直接填写现金流量数据，不分列现金流入和现金流出而统称为现金流量时，现金流出用负数表示。
    • 2.资金等值的计算公式
      • 复利情况下
      • 1）一次支付现金流量等值计算
        • 一次支付
        • 已知现值求终值
        • 已知终值求现值
        • 总结
          • [结论12]一次支付终值系数（1＋i）n和一次支付现值系数（1＋i）-n互为倒数关系。即（1＋i）n×（1＋i）-n=1。
          • [结论13]在P一定，n相同时，i越高，F越大；在i相同时，n越大，F越大。在F—定，n相同时，i越高，P越小；在i相同时，n越大，P越小。
          • [结论14]在工程经济评价中，需要正确选取折现率，并注意现金流量的分布情况。在不影响技术方案正常实施的前提下，尽量减少建设初期投资额，加大建设后期投资比重。
      • 2）等额支付系列现金流量等值计算
        • 年金支付
        • 『提示5』在5期时间序列的每期期末均发生现金流量A，A称为年金，是发生在（或折算为）某一特定时间序列各计息期末（不包括第1期期初，即0期）的等额资金系列的价值。
          • 『注意』计算价值的时点；计算期数n为A的个数；时间点是指的年末。
        • （1）等额支付系列终值计算
          • 每年投入A，求未来F有多少
        • （2）偿债基金的计算（已知F、i、n，求A）
          • 已知未来要还F，每年存多少
          • 『结论15』式中：称为偿债基金系数，用符号（A/F，i，n）表示。故偿债基金计算公式可表示为：
          • 『结论16』年金终值系数和偿债基金系数互为倒数关系。
        • 算的是未来F与年金A的关系
        • （3）年金现值
        • （4）资金回收计算（已知P、i、n，求A）
          • 现在投入一笔资金，在资金时间价值作用下，一定期限内每年年末等额回收一笔资金，使收回的资金总额等于现在投入的资金及其增值额之和。银行发放贷款然后分期等额回收是资金回收的典型应用。
        • 算的是现值P与A的关系
• 1.3.3等值计算公式应用要点
  • 1)合理选取收益率
    • 一要合理选取收益率i进行经济分析，依据过高或过低的收益率进行经济分析的结果会影响决策的科学性和合理性；
    • 二要在规划各项现金流量（资金收付）安排时，应尽量将现金流入往早期安排，尽量推迟现金流出的支付时间，以充分利用资金时间价值。（早收晚付）
  • 2)正确认识等值计算系数的作用
    • 等值计算系数的作用在于将预计或实际现金流量换算到设定的同一个时点进行综合经济分析。
    • 这种计算不会导致预计或实际现金流量发生时间（时点）发生变动，也不会改变现金流量的方向。
  • 3)准确把握等值计算系数中的n
    • 一次支付等值计算系数中的n是时间序列中的期数；
    • 等额支付系列等值计算系数中的n是等额支付发生的次数。
  • 4)严格遵循现值P，终值F，年金A等值换算的对应关系
    • 一次支付
    • 年金支付
      • 『小结』等值点的确定
        • 1.原则：现值看头，终值看尾。
        • 2.运用：现值点和第一期年金间隔一期：P=A（P/A，i，n）终值点和最后一期年金时点重合：F=A（F/A，i，n）
  • 5)计息周期小于资金收付周期时等值计算的处理
    • （1）按收付周期的实际利率计算；
    • （2）按收益率（利率）i的时间单位（计息周期）计算。