The Bayesian Network Represent

"探索贝叶斯网络的强大表示力！本文从联合分布的实际挑战出发，揭示如何通过图结构捕捉概率依赖关系核心内容分为三部分：1）贝叶斯网络基础，阐释独立性假设与参数优化2）图与分布的映射理论，包括完美映射、最小I图及D分离准则3）分布P与图G的独立性等价性讨论，涵盖完备性与可靠性分析通过两大关键思想，展现概率模型与图论的精妙结合"。

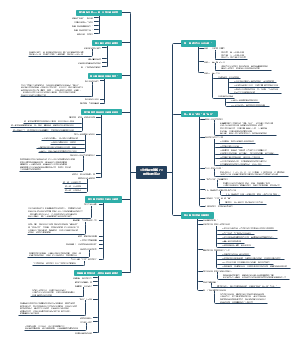
The Bayesian Network Representation

• 用所有参数表示联合分布不实际
  • N个二进制变量联合分布所需要的参数个数为
  • 计算量太大
  • 在统计上，估计这些参数不可能并且所需要的数据量太大
  • 在认知上，这些参数也不符合人类直觉
• Two key ideas
  • the representation of independence properties of the distribution
  • the use of an alternative parameterization that allows us to exploit these finer-grained independencies
• 1 Exploiting Independence Properties
  • Independent Random Variables
  • The Conditional Parameterization
    • the conditional representation is more natural than the explicit representation of the joint.
  • The Naive Bayes Model
• 2 Bayesian Networks
  • Bayesian networks build on the same intuitions as the naive Bayes model by exploiting conditional independence properties of the distribution in order to allow a compact and natural representation
  • Model(from P to G)
    • a directed acyclic graph (DAG)
      • nodes: rondom variables
      • edges: direct influence of one variable on another
      • This graph G can be viewed in two very dierent ways
        • a data structure
          • provides the skeleton for representing a joint distribution compactly in a factorized way;
        • a compact representation
          • for a set of conditional independence assumptions about a distribution
        • these two views are, in a strong sense, equivalent
    • a set of local probability models
      • represent the nature of the dependence of each variable on its parents
      • conditional probability distribution (CPD) for r.v. X given its parents
      • joint probability
        • the chain rule for Bayesian networks
    • Reasoning Patterns
      • causal reasoning
      • evidential reasoning
      • intercausal reasoning
  • A formal semantics (from G to P)
    • Basic Independencies
      • a node depends directly only on its parents
        • why???
    • Bayesian network structure
  • Graphs and Distributions(G == P?)
    • A distribution P satisfies the local independencies associated with a graph G if and only if P is representable as a set of CPDs associated with the graph G
    • I-Maps
      • I-Map to Factorization
        • every distribution for which G is an I-map must satisfy these assumptions
      • factorization
        • Bayesian network
          • specifies the completeness??
        • Thm 1
          • the conditional independencies imply factorization
      • Factorization to I-Map
        • Thm 2
          • Thm1 and Thm2 imply the if and only if above
• 3 Independencies in Graphs
  • Are there other independencies that hold for every distribution P that factorizes over G?
  • D-separation
    • Direct connection
    • Indirect connection
      • Indirect causal effect/Causal trail
        • X->Z->Y
          • active if and only if Z is not observed
      • Indirect evidential effect/Evidential trail
        • Y->Z->X
          • active if and only if Z is not observed
      • Common cause
        • X<-Z->Y
          • active if and only if Z is not observed
      • Common effect/v-structure
        • X->Z<-Y
          • active if and only if either Z or one of Z's descendants is observed
    • The definition of observed variable and active trail
    • The definition of d-sepertation
      • global Markov independencies I(G)
  • Soundness and Completeness
    • Soundness
      • the first property we want to ensure for d-separation as a method for determining independence is soundness
        • if we find that two nodes X and Y are d-separated given some Z, then we are guaranteed that they are, in fact, conditionally independent given Z
      • Thm 3
        • i.e. any independence reported by d-separation is satisfied by the underlying distribution.
    • Completeness
      • d-separation detects all possible independencies
      • faithful
      • Thm 4
        • • this can only conduct from the given G,but if the G cannot reflcets all the dependencies, we cannot deduce that I(P) is the subset of I(G) except faithful is fullfilled
      • Thm 5
    • An Algorithm for d-Separation
    • I-Equivalence
      • very dierent BN structures can actually be equivalent, in that they encode precisely the same set of conditional independence assertions
      • The definition of I-equivalent
        • this is a equivalence relation
        • any distribution P that can be factorized over one of these graphs can be factorized over the other.
      • skeleton
        • definition
          • but the two networks have the same trails is clearly not enough,such as v-structure
        • Thm7
          • attention: this characterization is not an equivalence,this the sufficient condition for I-equivalence
            • example : complete graph
      • immorality
        • definition
        • Thm8
        • cover edge
        • Thm 9
• From Distributions to Graphs
  • Given a distribution P , to what extent can we construct a graph G whose independencies are a reasonable surrogate for the independencies in P?
  • Minimal I-Maps
    • definition
    • how to get it?
      • Algorithm
    • notation
      • G is a minimal I-map for P is far from a guarantee that G captures the independence structure in P
  • Perfect Maps
    • definition
    • find the P-map
      • Is whether every distribution has a perfect map?NO!
        • deterministic relationships can lead to distributions that do not have a P-map
        • A dierent class of examples is not based on structure within a CPD, but rather on symmetric variable-level independencies that are not naturally expressed within a Bayesian network
        • A second class of distributions that do not have a perfect map are those for which the independence assumptions imposed by the structure of Bayesian networks is simply not appropriate
      • EXIST, how to find it?
  • Finding Perfect Maps
    • one of our tasks in this section is to develop a compact representation of an entire equivalence class of DAGs
    • 1 Identifying the Undirected Skeleton
      • lemma 1
      • lemma 2
    • 2 Identifying Immoralities
      • Proposition 1
      • Proposition 2
    • 3 Representing Equivalence Classes
      • the definition of class PDAG
      • Rules for class PDAG
      • Thm10
      • Proposition 3
      • Proposition 4
      • Proposition 5
      • Proposition 6
      • Proposition 7
      • Proposition 8