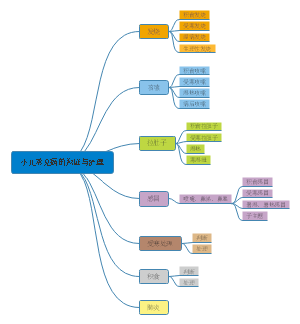
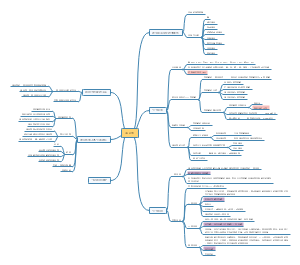
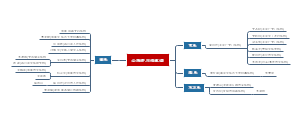
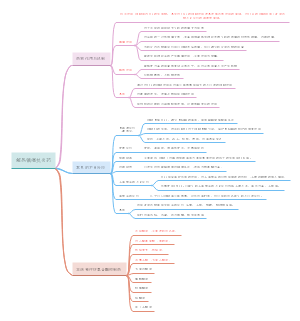
医学统计学思维导图

详细概述了医学统计学的主要内容和关键步骤。在“统计描述”部分详细讨论了统计描述的表达方式，包括绪论、统计推断、同质与变异、变量与数据类型、基本概念、总体和样本、误差、概率与运算法则、定量数据以及特定数据类型的统计描述等。在“统计推断”部分，介绍了正态曲线和正态分布的特征，布局清晰，内容丰富，涵盖了医学统计学的主要知识点和流程，对于理解和应用医学统计学具有重要的指导意义。

医学统计学

• 绪论
  • 作用
    • 研究对象
      • 医学中具有不确定性的事物
    • 主要作用
      • 通过数据的偶然性揭示内在规律性
    • 要点
      • 正确的选用统计分析方法，结合专业知识做出科学的结论
  • 基本内容
    • 统计设计
      • 实验分组、抽样方法、样本量估计、数据管理、统计分析方法等
    • 数据整理与核查
      • 数据编码
        • 系统化：分组、归纳、汇总等
      • 数据核查
        • 净化：清理、核对、纠错等
    • 统计描述表达方式
      • 统计指标
      • 统计表
      • 统计图
    • 统计推断
      • 参数估计
        • 用样本统计量估计总体参数分为点估计和区间估计
      • 假设检验
        • t检验、ANOVA、x²检验、秩和检验
        • 作用：能够辨别出由随机波动引起的差别的概率大小
        • 目的：比较总体参数有误差别
  • 基本概念
    • 同质与变异
      • 同质：指观察单位或研究个体间具有相同或相近的性质，通常要求主要研究指标的影响因素相同或基本相同
        • 观察单位是研究对象的基本单元，即为一个患者或一份生物样品
      • 变异：是指同一种测量在总体中不同观察单位或个体之间的差别
    • 变量与数据类型
      • 变量
      • 数据类型
        • 定量数据（计量资料）
        • 定性数据（计数资料）
        • 有序数据（等级资料）
    • 总体和样本
      • 总体指研究对象的全体，通常由所有的同质观察单位或个体组成
      • 样本指从总体中选取的有代表性的一部分观察单位或个体，通常使用随机选取方法得到
    • 误差
      • 非随机误差
        • 系统误差
        • 过失误差
      • 随机误差
        • 随机测量误差
        • 抽样误差
    • 概率与运算法则
      • 范围：0≤P≤1
      • 习惯上将P≤0.05的事件称为小概率事件
      • 乘法法则
      • 加法法则
      • 条件概率
      • Bayes公式
• 统计描述
  • 特定数据类型的统计描述
    • 定量数据
      • 频数分布
        • 表示方式
          • 频数表
          • 直方图
        • 作用
          • 揭示资料的分布类型（对称、正偏态、负偏态）
          • 解释资料的分布特征（离散、集中）
      • 描述集中趋势的统计学指标
        • 算术均数
          • 适用条件:正态或近似正态分布资料
          • 计算方法
            • 直接法(小样本，原始资料）
            • 加权法（大样本或频数表资料)
        • 几何均数
          • 适用条件：等比资料或对数正态分布资料
          • 计算方法
            • 直接法（小样本，原始资料）
            • 加权法（大样本或频数表资料）
        • 中位数和百分位数
          • 适用条件：偏态分布资料，开口资料和分布不明的资料
      • 描述变异程度的统计学指标
        • 极差
          • 适用范围：任何计量资料
          • 优点：计算简便
          • 缺点：n大，R也会大
        • 四分位数间距
          • 适用条件：与中位数匹配描述
          • 优点：一组变量中间50%变量的极差
          • 缺点：仍未考虑到每个观察值
          • Q=P75-P25
        • 方差与标准差——X~N(μ，σ²）
          • 适用条件：与均数匹配使用。用于对称分布，尤其正态分布
          • 表示方法
            • 总体方差、总体标准差用σ、σ²表示
            • 样本方差、样本标准差用S、S²表示
        • 变异系数——CV
          • 适用条件：比较观察指标单位不同或均数相差较大的资料变异程度
          • CV=S/X×100%
    • 定性数据
      • 常用相对数（比值）
        • 率
          • 表示在一定空间或时间范围内某现象的发生数与可能发生的总数之比
          • 说明某现象出现的强度和频率
          • 率=比例基数=某事物或现象的实际发生数/可能发生该事物或现象的个体总数×比例基数K【π总体率，p样本率】
        • 构成比
          • 表示某事物内部各组成部分在整体中所占的比重，常以百分数表示
          • 构成比=某一组成部分的观察单位数/同一事物各组成部分的观察单位总数×100%
        • 相对比
          • A、B两个有关联指标值之比，用以描述两者的对比水平
          • 相对比=A/B
          • 分类
            • 两类别例数之比
            • 相对危险度（RR)
            • 比数比（OR)
        • 标准化率
          • 采用某影响因素的统一标准构成，以消除构成不同对率的影响，使标准化后的标准化率具有可比性
          • 标准的选择原则
            • 1.两组之一
            • 2.两组合计
            • 3.另选其他，通用的或便于比较的标准
      • 医学常用的相对数指标
        • 死亡统计指标
          • 死亡率
            • 死亡率=某年某地死亡人口数/同年该地平均人口数×1000‰
            • 分母等于年中人口数=（年初人口数+年末人口数）/2
          • 死亡专率
        • 疾病统计指标
          • 发病率
            • 发病率=某时期某病新病例数/同期间内平均人口数×比例基数
            • 罹患率——特殊发病率
          • 患病率（某地）
            • 患病率=发病率×病程（P=I*D)
          • 病死率、治愈率、存活率、感染率、续发率
      • 相对数指标使用的注意问题
        • 不要把构成比与率相混淆
        • 使用相对数时分母不宜过小
        • 正确合并估计率指标
        • 注意资料可比性
        • 样本率或构成比存在抽样误差
• 正态分布与医学参考值范围
  • 正态分布
    • 正态曲线
      • 中间高，两边低，左右对称，略称钟形
    • 正态分布的特征
      • 对称性：以X~μ为中心，左右完全对称，并以X轴为渐近
      • 集中性：单峰，在X=μ处曲线最高，在μ±σ各有一个拐点
      • 两个参数
        • μ：位置参数，决定正态分布曲线的中心位
        • σ：形态参数，决定正态分布曲线的高矮胖瘦
      • 面积分布呈一定规律（对称区域面积相等）
        • 曲线下的面积即为概率
        • 曲线下的总面积为1或100%
        • 区间μ±σ面积为68.27%
        • 区间μ±1.96σ面积为95.00%
        • 区间μ±2.58σ面积为99.00%
    • 标准正态分布：Z分布，Z~
      • 任意正态分布，X~N(μ，σ²),令Z=X-μ/σ，则Z~N（0,1）的标准正态分布
      • Z界表值用途
        • 根据Z值查左侧尾部面积（概率）
        • 根据左侧尾部面积（概率）查Z
    • 正态分布的应用
      • 估计变量值的概率分布
      • 制定医学参考值范围
      • 质量控制
      • 许多统计分析方法的理论基础
  • 医学参考值范围
    • 制定注意事项
      • 确定同质的参照总体
      • 选择足够例数的参照样本
      • 控制检测误差
      • 选择单、双侧界值
      • 选择适当的百分数范围
      • 选择计算参考值范围的方法
    • 计算方法
      • 正态分布法（服从正态或近似正态分布）
      • 百分位数法（任何分布类型的资料）
• 统计表与统计图
  • 统计表
    • 结构——标题、标目、线条、数字、备注
    • 分类
      • 简单表（一个分类变量）
      • 组合表（两个及以上分类变量)
  • 统计图
    • 结构——标题、标目、图域、图例、刻度
    • 分类
      • 描述定量数据
        • 直方图
          • 连续型数值变量频数分布
          • 注意事项
            • 纵轴刻度必须从0开始
            • 矩形面积代表各组段频数或频率
        • 线图
          • 描述统计量随时间变化而变化的趋势
          • 分类
            • 普通线图——反映不同指标变化的幅度
            • 半对数线图——反映不同指标变化的速度
        • 箱式图
          • 比较两组或多组偏态分布资料的特点
          • 特点——纵轴可以不从0开
        • 误差条图
          • 反映均数和可信区间
      • 描述定性数据
        • 直条图
          • 表示相互独立的某统计指标值
          • 分类
            • 单式直条图
            • 复式直条图
          • 特点——直条图的纵轴起点必须为零
        • 构成图
          • 适合描述分类变量的构成比
          • 分类
            • 圆图——用于一组资料内部构成比
            • 百分条图——用于多组资料构成比的比较
      • 描述双变量数据——散点图
• 统计推断
  • 参数估计
    • 由样本统计量估计总体参数的大小（量的推断）
    • 抽样误差
      • 均数（定量资料）
        • 均数的抽样分布
          • 中心极限定理
            • 一般只要n≥30，可认为样本均数服从正态分布
          • 正态总体抽样的抽样分布规律
            • 样本均数的分布以μ为中心，左右基本对称
            • 其变异程度大大减小，n越大，样本均数的变异程度越大
          • 偏态总体抽样的抽样分布规律
            • 样本含量大时，样本均数的分布仍近似正态分布
        • 均数的抽样误差
          • 产生原因
            • 总体中个体差异大小即σ的大小
            • 抽取的样本含量大小即n的大小
          • 表现形式
            • 样本均数彼此间的差异
            • 样本均数与总体均数间的差异
          • 衡量标准——均数的标准误差
            • 概念：样本均数的标准差
            • 符号：σx(理论值），Sx（估计值)
            • 作用
              • 反映抽样误差的大小
              • 用于确定总体均数的可信区间
      • 率（定性资料）
        • 率的抽样分布
          • n较小时，样本率的抽样分布呈离散型分布
          • 当n足够大，样本率的抽样分布逼近正态分布
            • 一般n,p和n(1-p)＞5
        • 率的抽样误差
          • 表现形式
            • 样本率彼此间的差异
            • 样本率与总体率间的差异
          • 衡量标准——率的标准误
            • σp(理论值），Sp（估计值）
            • π已知，用理论值，否则，用估计
          • 方法
            • 点估计
            • 区间估计
              • 可信区间
                • 准确度：1-α越接近1越好
                • 精密度：区间宽度越窄越好
              • 区间估计类型
                • 均数估计
                  • 通过样本均数对总体大小进行估计
                  • σ已知——z分布
                  • σ未知
                    • 大样本（n≥50）——z分布（t分布的极限为z分布）
                    • 小样本——t分布
                • 均数差值估计
                  • 通过两样本均数的差值对两个总体均数差值大小进行估计
                  • 自由度——v=n1+n2-2
                  • 两样本均数之差的标准误差——Sx1-x2
                • 总体率估计
                  • 小样本率：n≤50，查表法（二项分布）
                  • 大样本率：n p≥5且n(1-p)≥5
  • 假设检验
    • 比较总体参数间的有无差别（质的推断）
    • 基本问题
      • 判断两份样本之间的差异是抽样误差导致的，还是本质差异导致的
    • 基本原理
      • 反证法
      • 小概率事件原理
    • 基本步骤
      • 建立假设，确定检验水准
        • H0：原假设（零假设，无效假设）
        • H1：备择假设（研究假设）
        • α：检验水准
      • 选择检验方法，计算检验统计量
        • 定量数据
          • t检验
            • 适用数据：一组或两组样本均数的比较
            • 应用条件
              • 随机样本
              • 正态分布总体
              • 两独立小样本比较时，要求两总体方差相等
            • 单样本t检验
              • 目的
                • 推断未知总体均数μ和常数μ0有无差别
              • 方法
                • σ已知：z检验
                  • 计算z值，查z界值表中p
                • σ未知
                  • 大样本（N＞50）：Z检验
                  • 小样本：t检验
                    • 计算t值，求得相应t界值表中p
            • 配对样本均数t检验
              • 目的
                • 检验两相关样本均数所代表的两未知均数是否相等
            • 两独立样本均数比较t检验
              • 目的
                • 检验两独立样本均数所代表的两未知总体均数是否相等
              • 方法
                • n1≥50且n2＞50：大样本Z检验
                • n1≤50或n2≤50
                  • 两样本的方差齐性检验
                    • F检验
                      • 使用条件：两样本均来自正态总体
                      • F分布：正偏态，两个参数v1,v2
                  • 两总体方差不齐
                    • t'检验
                      • 小样本，两样本来自正态总体
                    • z检验
                      • σ已知
                      • σ未知的大样本资料（n＞50）
        • 定性数据
          • x²检验
            • 四格表资料的x²检验
              • 适用数据——四格表数据
              • n<40或T<1
                • Fisher确切概率法
                  • 计算四个数据变化的各种组合
                  • 计算检验值
                  • 确定p值
              • n≥40且T≥5时使用专用公式
              • n≥40且1≤T<5时使用校正公式
            • 配对四格表资料的x²检验
              • 目的：推断两个总体率有无差别
              • 特点：两种方法的差别由b,c两格数据来反映，a,d两格表示两法结果相同，不予考虑
            • R×C表资料的x²检验
              • 目的
                • 可用于多个独立样本率的比
                • 两个及多个独立样本构成比的比
              • 条件
                • 理论数不能太小，各格的T≥1且1≤T<5格子不宜多余总格子数的R×C的数量、
      • 确定P值，做出统计推断
        • P≤α，拒绝H0，接受H1，差别有统计学意义，可认为两总体有差别
        • P≥α，不拒绝H0，差别无统计学意义，即根据目前试验结果，尚不能认为两总体有差别
        • I型错误：拒绝实际上成立的H0，属于弃真的错误，犯这种错误的概率是α
        • II型错误：接受实际上不成立的H0，属于取伪的错误，犯这种错误的概率是β
        • 注意事项
          • n一定时，α增大，β减少；反之成立
          • 如要同时减小α和β，唯一可行的办法是增加n
    • 假设检验与参数估计的关系
      • 区别
        • 区间估计用于定量推断总体参数的范围
        • 假设检验用于定性推断总体参数是否不等
      • 联系
        • 置信区间可回答假设检验有无差别的问题
        • 置信区间可提供假设检验的不能提供的信息
        • 假设检验能提供确切的概率P值，置信区间不能提供