现代投资组合理论和资本市场理论

最小方差前沿，根据可行集中收益率和相关洗水的平面图可以得出，可行集最左边的点是有效的，右边所有的点都是无效的。如果把最左边的点都连在一起形成一条曲线，这条曲线成为最小方差前沿。在相同的收益率水平下，这条曲线上的组合具有最小方差。

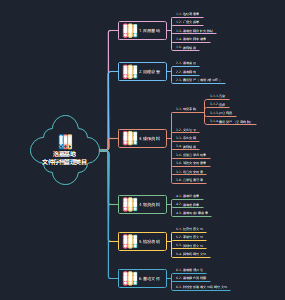
现代投资组合理论和资本市场理论

• 现代投资组合理论和资本市场理论的发展历程
  • ①均值-方差模型（哈里.马科维茨），1952年，他在《金融杂志》上发表了一篇题为“资产组合的选择”的文章中首次提出了均值-方差模型，奠定了投资组合理论的基础，标志着投资组合理论的开端。现代投资组合理论的核心思想是把多重证券的投资组合看做一个整体来进行分析和度量，然后把投资组合的风险分解为两部分--非系统风险和系统风险。
  • ②资本资产定价模型（威廉.夏普、约翰.林特耐和简.莫辛），三人分别独立研究出著名的资本资产定价模型（Capital Asset Pricing Model ，CAPM），CAPM对资产的收益、风险以及两者的关系进行了精确描述，并在一系列假设条件下就投资者行为得出如下结论：对所有投资者，最优的资产组合都是无风险资产和市场资产组合的组合。这种组合的所有可能情况形成一条直线，本称为资本市场线（Capital Market Line，简称CML）。现在，CAPM已经被广泛应用于度量各种风险证券或者风险证券组合的系统风险。
    • 资本市场线（Capital Market Line，简称CML）
      • 是指表明有效组合的期望收益率和标准差之间的一种简单的线性关系的一条射线。它是沿着投资组合的有效边界，由风险资产和无风险资产构成的投资组合。
      • 资本市场线可表达为： 总报酬率=Q*（风险组合的期望报酬率）+（1-Q）*（无风险利率） 其中 ：Q代表投资者自有资本总额中投资于风险组合M的比例，1-Q代表投资于无风险组合的比例。
  • ③套利定价理论（斯蒂芬.罗斯），他于1976年突破性地发展了CAPM，提出了套利定价理论（Arbitrage pricing theory，APT）。该理论认为风险资产的收益与多个共同因素之间存在线性关系，从而将单因子CAPM发展为多因子模型。APT的前提是完全竞争和有效资本市场。APT认为，只要任何一个投资者不能通过套利获得收益，那么期望收益率一定与风险相联系。
    • 套利
      • 套利亦称“利息套汇”。主要有两种形式：(1) 不抛补套利。即利用两国资金市场的利率差异，把短期资金从低利率的市场调到高利率的市场投放，以获取利差收益。(2) 抛补套利。即套利者在把短期资金从甲地调到乙地套利的同时，利用远期外汇交易避免汇率变动的风险。套利活动会改变不同资金市场的供求关系，使各地短期资金的利率趋于一致，使货币的近期汇率与远期汇率的差价缩小，并使资金市场的利率差与外汇市场的汇率差价之间保持均衡，从而在客观上加强了国际金融市场的一体化。但是大量套利活动的进行，会导致短期资本大规模的国际移动，加剧国际金融市场的动荡。
  • ④期权定价模型（费雪.布莱克与迈伦.斯科尔斯），于1973年运用随机微分方程理论推导出期权定价模型。
  • ⑤有效市场假说（尤金.法玛），1970年提出了有效市场假说（Efficient Markets Hypothesis，EMH），并且把有效市场分为以下三种不同类型：
    • ①强有效市场，指股价已反映了全部与公司有关的信息，包括所有公开信息及内部信息。
    • ②半强有效市场，认为股价已经反映了所有公开的信息。
    • ③弱有效市场，认为股价已反映了全部能从市场和交易数据中得到信息。
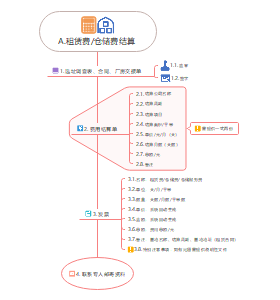
• 资产收益率的期望、方差、协方差、标准差等概念、计算和应用
  • ①单个或多个资产的期望收益率
    • 期望收益率又被称为平均收益率，是资产各种可能收益率的加权平均值。多个资产组成的投资组合的期望收益率为其所包含各个资产的期望收益率的加权平均。
  • ②单个资产的反差和标准差
    • 方差的标准差是估计资产手机收益率和期望收益率之间可能偏离程度的测度方法。
      • ​
      • ​
      • 式中：δ^2为方差；δ为标准差；ri表示该资产在第i种状态下的收益率；pi表示收益率ri发生的概率；n表示资产可能的收益状态的总数；E（r）表示该资产的期望收益率。
      • 如果每种状态可能性相同，那我们可以用1/n来代替概率pi，即：
        • ​
        • ​
      • 在实际应用中，常常用资产过去m期的收益率作为样本来估算该资产收益率的方差和标准差。样本的方差和标准差为：
        • ​
        • ​
        • 式中：-r为样本中m期收益率的均值。样本方差是对总体方差的无偏估计。
  • ③资产收益率的协方差和相关系数
    • 在投资组合理论中，使用协方差和相关系数测度两个风险资产的收益之间的相关性。
      • 协方差
        • 协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
    • 对于已知资产 i 和 j 的收益率的联合分布，其协方差为：
      • ​
      • 对于s种（ri，rj）的状态，假定每种状态的可能性为 pk ，k 状态下两种资产的收益率分别为rik 和 rk 。那么
        • ​
      • 若使用历史上m期样本计算资产 i 和 j 的收益率的协方差，则其公式为：
        • ​
      • 两个资产收益率的相关系数定义为协方差初一两个证券各自标准差的乘积，以希腊字母ρ表示：
        • ​
      • 相关系数的取值范围是「-1，+1」。相关系数<0，两变量为负线性关系；=0，无关系；>0，正。
  • ④投资组合收益率的方差和标准差
    • 投资组合收益率的方差和标准差，取决于各资产的反差、权重以及相互之间的相关系数。
    • ……
    • 单一资产方差不变，相关系数越小，资产组合的方差就越小。
• 资产收益相关性的概念、计算和应用
  • 对于由两个资产 i 和 j 构成的组合，给定一个特定的投资比例，则得到一个特定的投资组合，它具有特定的预期收益率和标准差，如图7-1的标准差-预期收益率平面中表现为一个特定的点。如果让投资比例在一个范围内连续变化，则得到的投资组合点在标准差-预期收益率平面中构成了一条连续曲线。给定不同的相关系数，得到不同的曲线。
    • ​
    • 当ρ=1时，……
    • 当ρ=-1时，……
      • 转折点即标准差为0的组合，等效于无风险资产。
    • 当ρ=0时，……
      • 相关系数月销，组合的曲线越往左边弯曲，组合风险越小（即在相同收益率的情况下，风险更小。），组合的效用越高。
• 均值-方差模型的基本思想
  • 马科维茨投资组合理论的基本假设是投资者是厌恶风险的。在这个假设下，他建立了一个投资组合分析的模型，其要点主要有：
    • ①投资组合具有两个相关的特征，一是预期收益率，二是各种可能的收益率围绕其预期值的偏离程度，这种偏离程度尅用方差度量。
    • ②投资者将悬着并持有有效的投资组合。
    • ③通过对每种证券的期望收益率、收益率的方差和每一种证券与其政权之间的相互关系（以协方差来度量）这三类信息的适当分析，可以在理论上识别出有效投资组合。
    • ④对上述三类信息进行计算，得出有效投资组合的集合，并根据投资者的偏好，从有效投资组合的集合中选择出最适合的投资组合。
• 有效前沿、无差异曲线和最优组合的概念
  • 可行集，代表市场上可投资产所形成的所有组合，亦称机会集。所有可能的组合都位于可行集的内部或边界上。
    • 可行集图1，待用Axglph制作，卡在了如何绘制曲线的问题上。
  • 最小方差前沿，根据可行集中收益率和相关洗水的平面图可以得出，可行集最左边的点是有效的，右边所有的点都是无效的。如果把最左边的点都连在一起形成一条曲线，这条曲线成为最小方差前沿。在相同的收益率水平下，这条曲线上的组合具有最小方差。
    • 在最小方差前言最左边的拐点处会有一条与纵轴平行的直线与最小方差前言相切，只有一个焦点，这个切点叫作全局最小方差组合。代表所有资产组合中风险最小的组合。
  • 有效前沿，从你全局最小方差组合开始，其上半部分被成为马科维茨有效前沿，简称有效前沿。有效前沿是能够达到的最优的投资组合的集合，它位于所有资产和资产组合的左上方。
    • 有效前沿上的投资组合为有效组合，其特点是包含了所有风险资产，所有成为有效组合是完全分散化的投资组合。
    • 如果一个投资组合是有效的，那么投资者就无法找到另外一个预期收益率更高且风险更低的投资组合。
  • 效用，是投资带给人的满意程度。假定每一个投资者可以根据资产（或资产组合）的预期收益与风险情况对效用进行量化比较，则可得出其效用函数。效用函数的常见形式为：
    • U=E(r)-1/2Aδ^2，式中：U 为效用值；A为某投资者的风险厌恶系数；E（r）为资产的预期收益；δ^2为资产收益的方差。
    • 根据投资者对风险不同的态度，可以将投资者分为风险中性、风险厌恶和风险偏好三类。
      • 风险中性的投资者仅根据期望收益这一个指标做投资决策，不关心风险。
      • 风险厌恶的投资者，在期望收益相同的投资方案中，会选择其中风险最小的。
      • 风险偏好的投资者，在期望收益相同的投资方案中，会选择其中风险最大的。
  • 无差异曲线，根据投资者的效用函数，可以画出无差异曲线。无差异曲线是在期望收益-标准差水平上由相同给定效用水平的所有点组成的曲线。
    • 无差异曲线，待用Axglph制作，卡在了如何绘制曲线的问题上。
    • 特点
      • ①风险厌恶的投资者的无差异曲线是从左下方向右上方倾斜的。
      • ②同一条无差异曲线上的所有点向投资者提供了相同的效用。
      • ③对于给定风险厌恶系数的某投资者来说，可以画出无数条不会交叉的无差异曲线。
      • ④风险厌恶程度高的投资者与风险厌恶程度低的投资者相比，其无差异曲线更陡，以为随着风险增加，其要求的风险溢价更高。
      • ⑤当向较高的无差异曲线移动时，投资者的效用增加。
  • 最优组合，指使投资者效用最大化的是无差异曲线和有效前沿相切的点所代表的投资组合。
    • 最优组合，待用Axglph制作，卡在了如何绘制曲线的问题上。
• 资本市场理论
  • 资本市场理论的前提假设
    • ①所有的投资者可以以无风险利率任意地借入或贷出资金。
    • ②所有的投资者都是风险厌恶者，都以马科维茨均值-方差模型分析框架来分析证券，追求效用最大值，购买有效前沿与无差异曲线的切点的最优组合。
    • ③所有的投资者的投资期限都是相同的，并且不在投资期限内对投资组合做出动态调整。
    • ④所有投资者的期望都是相同的，
    • ⑤所有的投资都可以无限分割，投资数量任意。
    • ⑥无摩擦市场（主要指没有税和交易费用）。
    • ⑦投资和是价格的接受者。
  • 市场均衡状态
    • ①所有投资者将选择持有包括所有证券资产在内的市场组合M。
    • ②市场组合处于有效前沿。
    • ③市场组合的风险溢价与市场组合的方差和投资者的典型风险偏好成正比。
    • ④单个资产的风险溢价与市场投资组合M的风险溢价和该资产的β系数成比例。β系数是衡量资产收益率相对市场组合收益率变化的敏感度的指标。
• 系统性风险和非系统性风险
  • 非系统性风险
    • 指能够通过构造资产组合分散掉的风险，是可以避免的风险。
  • 系统性风险
    • 指不能通过构造资产组合分散掉的风险；系统性风险是固定不变的。
  • 风险溢价
    • 指投资者要求在承担风险的时候得到的风险补偿。但是非系统性风险可以通过构造资产组合分散掉，因此，承担非系统风险，不能得到风险补偿。
      • 非系统性风险与系统性风险，待用Axglph制作，卡在了如何绘制曲线的问题上。
• 资本配置线和证券市场线
  • 资本配置线（CAL）
    • • ​
    • 资产配置线上的点表示无风险资产与风险资产 x 的线性组合，其截距是无风险资产收益率Rf，斜率是（E（Rf）-Rf）/δx，这个斜率就是风险自查你的夏普比率，也是这条CAL上任一点的夏普比率。
      • 函数图，待补充。
  • 资本市场线
    • 每一个投资者都有不同的最优投资组合及不同的CAL。有效前沿上的点表示所有投资和最优的风险资产组合。我们去无风险资产与有效前沿上的点相连，可以得到无数条CAL。在无数条CAL中，因为在相同的风险水平下，最优的CAL期望收益率最高的是与有效前沿相切的那条（即资本市场线，CML）。
      • 资本市场线从纵轴上无风险利率点Rf处向上延伸，与原马科维茨有效前沿曲线相切于点M，这条直线上包括了所有风险资产投资组合M与无风险资产的组合。当市场达到均衡时，切点M即市场投资组合，理论上，市场投资组合包括市场上所有的风险资产，并且其包含的各资产的投资比例与整个市场上风险资产的相对设置比例一致。
        • 函数图，待补充。
      • ​
  • 证券市场线
    • 预期收益率与β系数的关系式可以表示为证券市场线（SML），证券市场线描述了单个资产的风险溢价与市场风险之间的函数关系。可以用来判断一项资产的定价是否合理。
      • ​
      • 资本资产定价模型给的定价公式为：
        • ​
        • β系数为零的资产的预期收益率等于无风险收益率。
      • ​
        • 在实际操作中，CAPM的假设调价未必能得到满足。不是所有的投资者都会完全按照分散化的理念去投资，不同的投资者会对于各资产的预期收益率及风险的判断也不会完全一致。这将导致现实中各资产的预期收益率未必与CAPM的预测结果一致。CAPM解释不了的收益部分习惯上用希腊字母（α）来描述，有时称为“超额”收益。