大物实验

《大学物理实验（高等院校物理教材）》是2010年由清华大学出版社出版的图书，作者是郭悦韶等。图书简介 　本实验教材根据教育部颁发的《高等工业学校物理实验课程教学基本要求》，结合高校专业设置特点和实验设备的具体情况，

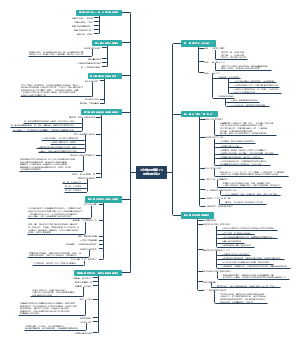
大物实验

• Measurement and Error
  • Basic concept of measurement and error
    • Measuring
      • Meaning of measuring
        • Measure
          • 
        • elements of measurement
          • Method，Accuracy，Object，Unit
      • Classification
        • According to the method
          • Direct measurement
            • basic
          • Indirect measurement
            • a large number of data
            • can be converted into direct measurement
        • According to the measurement conditions
          • Same precision measurement
    • Error
      • True value
      • Absolute error and relative error
        • Absolute error 绝对误差
          • True value
            • 
            • 
          • Known correction value
            • 
        • Relative error 相对误差
          • 
      • Sources of error
        • Instrument error
        • Method error
        • Enviromental error
        • Persons error
      • Classification of errors
        • Systematic error 系统误差
          • Features:certainty
          • Homodyne(零差) of micrometer screw/pointer voltmeter
        • Random error 偶然误差
      • Several related concepts of error
        • Precision---Random error
        • Accuracy---Systematic error
  • Estimate random error of direct measurement
    • Normal distribution for random error
      • single peak
      • boundedness
      • symmetry
    • Use arithmetic mean value as measurement result
      • 同一对象
      • 不同对象
    • Estimation error by standard deviation
      • 
    • Confidence probability and confidence limits
      • 
      • 
    • Excluding bad value
      • Pauta criterion
        • 
        • Mean value N and error S should be calculated after excluding the bad value, Until there is no bad value.
        • Note：N<10 is not reliable when using Pauta criterion.
• Measurement Uncertainty
  • Conception
    • Role
      • Quality assessment for measurements （ International standard ）
    • Implication
      • Because of error,the uncertainty degree of measurement result
  • Classification
    • A type uncertainty
      • Using statistical
    • B type uncertainty
      • Not using statistical
  • Calculations
    • Direct measurement
      • Table
      • Estimation error
        • Satisfy conditions?
          • NO: Enlarge the estimate error
          • Yes:Continuous reading instruments?
            • No: No estimation error
            • Yes: Estimate error
      • Instrument error
        • Labeling on the instrument
          • Vernier Caliper
        • Label accuracy class on the instrument
          • Pointer Meter
          • meaning of accuracy level
            • Resistance box
              • Numerator of percentage of maximum percentage error to measured value
            • Pointer meter
              • Numerator of Percentage of maximum error to full-scale values
        • Implied or instructions labeling
          • Ruler
        • Instrument error estimation
          • Continuous reading instruments
            • 
          • Discontinuous reading instruments
            • 
      • Single measurement
        • Often use single measurement
        • Conditions
          • No significant fluctuation measurements
      • Combined uncertainty
    • Indirect measurement
      • Total Differential of Multi-Function
        • 
      • Transfer expressions for uncertainty
        • 
      • Simplify calculation of Uncertainty principle to abandon the small error
        • Any one less than another one for 1/3 → Square less than 1/10 →ignore
  • Overall uncertainty
    • 
  • Expression of measurement result
    • 
  • 
• Significant numbers
  • Conception
    • In the measurement results ， consists of several reliable numbers and onesuspicious number， to be a Significant figures
  • Notes and expalnation
    • Significant figures of “0”
      • 0’ in the middle or at the end is significant
        • Can't add and delete“0”at the end of result!
      • In front of the decimal point“0” and behind the point“0”invalid
        • When unit conversion,the same number of significant figures
    • Values in scientific notation
      • 
      • Data into appropriate units more concise, more readable
    • Relationship between instrument and significant figures
      • Significant figures are determined by the accuracy of theinstrument range and the measured quantity
  • Determine significant figures of the direct measurement-how to read
    • General rules
      • A Instrument error known-result has the same bit as that ofinstrument error or one more bit
    • 
  • Determine significant figures of the indirect measurement-algorithms
    • Addition and Subtraction
      • Leave the same number of decimal places in theanswer as there are in the quantity with leastnumber of decimal places答案小数点后小数位数与所给数据小数点后小数位数最小的数相同
    • Multiplication and division
      • Leave as many significant figures in the answer as thereare in the quantity with the least number of significantfigures在答案中留下有效数字的个数与所给数据有效数字个数最少的个数相同
    • Power and roots
      • Significant figures are the same as its substrate or square root有效数字与所给底物或平方根的有效位数相同
    • logarithm
      • Lg x mantissa and x have the samenumber of significant figures.Lgx的小数部分和x的小数部分有效位数相同
    • functions
      • Significant figures are determined by transfer relationship of uncertainty
    • Natural numbers and constants
      • Significant figures are infinite
        • Constants A e significant figures take the least or one moresignificant figures involved in computing quantity
• Data Processing
  • Table
    • clear, order, concise
    • Indirect measurement values in the table must be listed after the tablewith complete calculation process; if it is the same calculation, one completecalculation must be listed.
  • Drawing method
    • intuitively, regularly, subjective and arbitrary large (roughly
    • function
      • Average performance
      • Seeking empirical formula
      • Interpolation and Extrapolation内插和外推
      • Calibration curve校准曲线
        • Fold line connected with the line section between points
      • Curve linearization
        • 
        • 
        • 
    • Mapping rules
      • 
      • 
      • 
      • 
      • 
      • 
      • Axis no need the same ratio
      • Axis no need through zero
      • Scale simple, No need follow significant figure rule
      • Greater the slope, smaller the horizontal data spacing
    • Find linear equations
      • Not use experiment data, use data on the both sides of fitting line
      • Read conditions by grid's 1/10, meets the rule of significant figures
      • Completely process in calculating the slope and intercept
  • Successive minus method
    • relatively simple and objective, but the argument should be equal intervals, less rigorous
    • Divided into two groups, Subtract corresponding items
      • 
    • Applications
      • Odd data exit, delete first\last\middle data
      • Successive minus of numerator and denominator at the same time
  • Least sauqres method
    • objective rigorous,but more complex
    • Regression Analysis
      • Processing data by the statistical, so as to determine its function by calculation
      • Step
        • Infer functional form(regression functions)
          • 
        • Determine the parameters with experimental data to find best a, b, c
          • Least squares method
        • Test the function resonale or not using experimental data
          • Calculate the correlation coefficient equal to 1 or not
    • Find linear equation using least squares
      • 这个公式好像是错的
    • Correlation coefficient
      • 
    • Notes and examples
      • 6 steps, include formula, process, results, and significant figures
      • Not meet significant figures rule, Keeping more bits
      • Correlation coefficient |r| close to 1, intercept a last position same as y
      • Slope b significant figures the same as that of slope b' calculated by first and last data
  • Computer-aided process data
    • overcome the arbitrariness ofmapping method, but also make the complicated least square methodvery simple