导图社区 collage physics chapter 1~2
- 31
- 1
- 0
- 举报
collage physics chapter 1~2
这是一篇关于collage physics chapter 1~2的思维导图,便于理解课本,有助于期末考试复习和背诵。
编辑于2022-10-04 20:43:46 陕西- 相似推荐
- 大纲
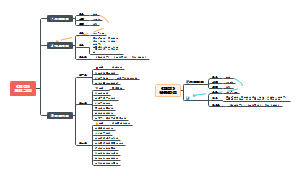
AP Physics
Unit 2
Motion in One Dimension
Displacement, Velocity, and Acceleration
Displacement
Motion invovles the displacement of an object from one place in space and time to another
SI unit: meter
Velocity
the average speed of an object over a given time interval is the length of the path it travels divided by the total elapsed time
Average speed = path length/elapsed time
SI unit: m/s
graphical interpretation of velocity
the position versus time graph
instantaneous velocity
the slope of the line tangent to the position versus time curve at " a given time" is defined to be the instantaneous velocity at time,
the intantaneous speed of an object, which is a scalar quantity, is defined as the magnitude of the instantaneous velocity.
Acceleration
when the object's velocity and acceleration are in the same direction, the speed of the object increases with time
instantaneous acceleration
the instantaneous acclereation a is the limit of the average acceleration as the time intrval Δt goes to zero
the instantaneous acceleration of an object at a given time equals the slope of the tangent to the velocity versus time grapgh at that time
Motion Diagrams
a motion diagram is a representation of a moving object ar successive time intervals
a motion diagram is analogous to images resulting from a stroboscopic phorograph of a moving object
One-Dimensional Motion with Constant Acceleration
when one object moves with constatn acceleration, the instantaneous acceleration at any point in a time intercal is equal to the calue of the acerage acceleration over the entire time interval
the average acceleratoon equal to the instantaneous acceleration when a is constant
the area under the graph of v versus t for any object is equal to the displacement Δx of the object
Freely Falling Objects
a feely falling object is any object moving freely under the influence of gravity alone, regradless of its initial motion
gravitational acceleration
g
at earth's surface , thecalue of g is approximately 9.8 m/s^2,for quick estimates we use g ≈10m/s^2
Unit 1
Units
Standrads
The standard system of units for the fundamental quantities of sicence, called SI (System International).
Length
The SI unit of the length is the Meter
The meter was redefined as the distance traveled by light in vacuum during a time interval of 1/299792458 second.
Approximate values of Some Measured Lengths
Observable Universe
1*10^26 meter
Earth to Andromeda Earth to proxima
2*10^22 meter
Centauri
4*10^16 meter
One light-year
9*10^15 meter
Earth to Sun
2*10^11 meter
Earth to Moon
4*10^8 meter
Radius of Earth
6*10^6 meter
World's tallest building
8*10^2 meter
Football field
9*10^1 meter
Housefly
5*10^-3 meter
Typical organism cell
1*10^-5 meter
Hydrogen atom
1*10^-10 meter
Atomic nucleus
1*10^-14 meter
Proton diameter
1*10^-15 meter
Mass
The SI unit of mass is the Kilogram
The kilogram is defined as the mass of a specific platinumiridium alloy cylinder kept at the International Bureau of Weights and Measures at Sevres
Approximate Vlues of Some Masses
Observable Universe
1*10^52 kg
Miky Way galaxy
7*10^41 kg
Sun
2*10^30 kg
Earth
6*10^24 kg
Moon
7*10^22 kg
Shark
1*10^2 kg
Human
7*10^1 kg
Frog
1*10^-1 kg
Mosquito
1*10^-5 kg
Bacterium
1*10^-15 kg
Hydrogen atom
2*10^-27 kg
Electron
9*10^-31 kg
Time
The SI unit of time is the Second
The second is now defined as 9192631700 times the period of oscillation of radiation from the cesum atom
Approximate Vlues of Some Time Intervals
A period is defined as the time required for one complete vibration
Age of Universe
5*10^17 s
Age of Earth
1*10^17s
Age of college student
6*10^8 s
One year
3*10^7 s
One day
9*10^4 s
Heartbeat
9*10^4 s
Audible sound wave prtiod^a
1*10^-3 s
Typical radio wave period^a
1*10^-6 s
Visible light wave period^a
2*10^-15 s
Nuclear collision
1*10^-22 s
Some Prefixes for Powers of Ten used with metric (SI and cgs) Units
The centimetre–gram–second system of units (abbreviated CGS or cgs) is a variant of the metric system based on the centimetre as the unit of length, the gram as the unit of mass, and the second as the unit of time.
10^-18
atto-
a
10^-15
femto-
f
10^-12
pico-
p
10^-9
nano-
n
10^-6
micro-
μ
10^-3
milli-
m
10^-2
centi-
c
10^-1
deci-
d
10^1
deka-
da
10^3
kilo-
k
10^6
mega-
M
10^9
giga-
G
10^12
tera-
T
10^15
peta-
P
10^18
exa-
E
the Building Blocks of Matter
atoms
electron
nucleus
proton
the proton is nature's most common carrier of positive charge, equal in magnitude but opposite in sign to the charge on the electron
neutrons
the neutrons have no charge and has a mass about equal to that of a proton
once believed to be the smallest particle of matter but since foud to be a composite of more elementary particles
Dimensional Analysis
one way to analyze such expression
dimensions can be treated as algebraic quantities
Dimensions and Some Units of Area, VolumE, and Accelration
distance x has the dimension of length [x]=L,Time t has dimension [t]=T,velosity v has the dimensions length over time:[v] = L/T, and acceleration the dimensions length divided by time squared [a] = L/T^2
SI
Area (L^2)
m^2
Volume(L^3)
m^3
Velosity(L/T)
m/s
Acceleration(L/T^2)
m/s^2
cgs
Area (L^2)
cm^2
Volume(L^3)
cm^3
Velosity(L/T)
cm/s
Acceleration(L/T^2)
cm/s^2
U.S.customary
Area (L^2)
ft^2
Volume(L^3)
ft^3
Velosity(L/T)
ft/s
Acceleration(L/T^2)
ft/s^2
uncertainty in Measurement and Significant FIgures
All measurements are subject to uncertainty
No quantity of any substance can be determined with perfect accuracy
When there are many digits in a calculator, only a few of them are meaningful and valuable
Multiplication and division
When two or more quantities are multiplied (divided), the number of significant digits in the final product (quotient) is the same as the number of significant digits in the least accurate factor of the factors being combined, where least accurate means the least number of significant digits.
Addition and subtraction
For addition and subtraction, it is best to focus on the number of decimal places involved rather than the number of significant digits. When numbers are added (subtracted), the resulting number OF decimal places should be equal to the smallest number OF decimal PLACES in any of the terms IN the sum (difference).
Unir Conversions for Physical Quantites
The conversion factor between SI and American customary length units
1 mi = 1 609 m = 1.609 km
1 m = 39.37 in. = 3.281 ft
1 ft = 0.3048 m = 30.48 cm
1 in. = 0.025 4 m = 2.54 cm
Trigonometry
Estimates and Order-of-Magnitude Calculations
getting an exact answer to a calculation may often be difficult or impossible
The approximation is called an order of magnitude estimate and requires finding the nearest power of 10 to the actual value of the quantity
The symbol ~ means "on the order of" or "is approximately",
Coordinate System
basic information
a fixed reference point O is called origin
a set of specified aces, or directionsm with an appropriate scale and labels on the axes
instructions on labeling a point in space relative to the origin and axes
defination
a point on a line can be located with one coordinate, apoint in a plane with two coordinates
positive x is usually selected a stight of the origin and positive y upward from the origin
Trigonometry Review
sine
sinθ
side opposite θ/ hypotenuse
y/r
cosine
cosθ
side adjacent to θ/ hypotenuse
x/r
tangent
tanθ
side opposite θ/ side adjacent to θ
y/x
pythagorean theorem
r^2=x^2+y^2
Vectors
Vectors
quantity
vactor quantity
a vector quantity is characterized by having both a magnitude and a direction,
scalar quantity
a scalar quantity has magnitude, but no direction
equality of two vectors
adding vectors
Triangle method of addition
communtative law of addition
negative of a vector
subtracting vectors
multiplying or dividing a vector by a scalar
Components of a Vector
adding vectors algebraically