统计学作业

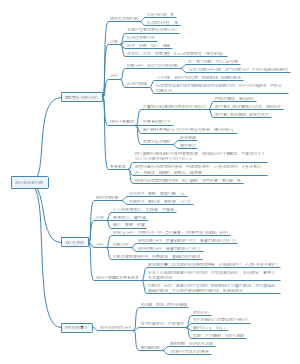
预防医学统计学，数值变量资料、分类变量资料的统计分析。

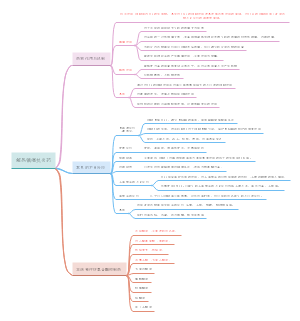
统计学

• 数值变量资料的统计分析
  • 统计描述
    • 集中趋势
      • 算数均数
      • 几何均数G
      • 中位数M
      • 百分位数Px
    • 离散趋势
      • 全距(极差)
      • 四分位数间距(P25－P50－P75)
      • 离均差平方和、方差、标准差
      • 变异系数
        • CV=S/V×100%
    • 正态分布及参考值范围
  • 统计推断
    • 标准误
      • • S一定 n↑ 标准误↓
    • t分布
      • 单峰分布以0为中心，左右对称，类似于标准正态分布
    • 参数估计
      • 点估计
        • 样本 均数X、S、P→总体μ、σ、π
        • 低把握度
      • 区间估计
        • σ已知，或σ未知但足够大，按Z分布
          • 双侧时100(1－α)%置信区间
          • 单侧时
        • σ未知，按t分布
          • 双侧时100(1－α)%置信区间
          • 单侧时
    • 假设检验
      • 步骤
        • 1.选择检验方法，建立检验假设并确定检验水准
          • H0:原假设(无效假设)
          • H1:对立假设(备择假设)
          • α常取0.05或0.01
        • 2.计算统计量
        • 3.确定P值
          • 若P≤α，拒绝H0,接受H1
          • 若P＞α，不拒绝H0
        • 4.作推断结论
          • 第Ⅰ类错误(弃真错误)，概率为α
          • 第Ⅱ类错误(取伪错误)，概率为β
          • 增加样本量n，可以同时减少两类错误
      • 检验方法
        • Z检验
          • 样本含量n较大(n≥100) n虽小但总体标准差σ已知
        • t检验
          • 总体标准差σ未知 样本含量较小(n＜100) 样本来自正态总体 两样本均数比较时方差齐
            • 配对t检验
            • 成组设计两样本均数的比较
            • 样本均数与总体均数的比较
        • 方差分析(ANOVA)
          • 变异的分解
          • • 用于多个均数的比较
          • 应用条件:正态，方差齐
• 分类变量资料的统计分析
  • 统计描述
    • 常见数据形式:绝对数
    • 常见相对数
      • 率
      • 构成比
      • 相对比
    • 率的标准化
      • 直接法
      • 间接法
  • 统计推断
    • 总体率的估计
      • 率的抽样误差和标准误
      • 可信区间估计
        • 正态近似法
          • n足够大，np、n(1－p)均大于5时
        • 查表法
          • n较小(n≤50)，p接近0或1
    • 率的Z检验
      • 样本率与总体率的比较
      • 两个样本率的比较
      • 率的多重比较
        • Scheffe'可信区间法
        • Bonferroni检验水准调整法
    • X²检验
      • 基本思想
        • 理论频数T=(行合计×列合计)/总例数
      • 四格表资料
        • n≥40且T最小≥5时用X²检验基本公式或四格表专用公式
        • n≥40,1≤T最小＜5时，用校正公式
        • n＜40或T最小＜1时，用确切概率法
      • 配对资料
        • b+c＞40时用基本公式
        • 25＜b+c＜40时用校正公式
        • b+c＞25时用确切概率法
      • 行乘列表资料
        • 检验统计量
        • 多个样本率的比较
          • H0:π1=π2=π3，即……有效率相等
          • H1:……不全相等
        • 两组构成比的比较
          • 双向无序
          • 单向有序
            • 比较效应有无差别，可用CMN法
            • 也可进行秩和检验，Ridit分析等
        • 多组构成比的比较
        • 关联性检验
          • 定性资料
          • R×C列联表
            • 双向无序列联表
              • 计算Pearson列联系数C
            • 双向有序且属性不同的列联表
              • Spearman秩相关、CMH中非零相关
            • 双向有序且属性相同的列联表
              • Kappa检验
      • 线性趋势检验
• 非参秩和检验
  • 基本思想
    • 基于秩次，通过编制，用秩次代替原始数据信息进行检验
  • 配对设计两样本
    • 二分类资料
      • NcNemar配对检验
    • 不满足参数检验条件
      • Wilcoxon符号秩和检验
    • 数值变量资料
      • t检验
  • Wilcoxon符号秩和检验
    • 用于配对样本差值的中位数和0比较
    • 单个样本中位数M和总体中位数M0比较
    • 两个独立样本比较
      • 查表法
        • n1≤10和n2-n1≤10时，查T界值表
      • 正态近似法
        • n1＞10或n2-n1＞10时，可用正态近似法做Z检验
        • 相同秩次较多(超过25%)，进行校正
      • Mann–Whitney U检验
  • 多样本比较的秩和检验
    • Kruskal–Wallis H检验
      • 建立假设检验
        • H0:……总体分布位置相同
        • H1:……总体分布位置不全相同
      • 计算统计量H值
        • 存在相同秩时，进行校正
      • 确定P值，作出判断
        • 查H界值表
          • 样本个数g=3，样本例数n≤5时
        • 查X²界值表
          • g=3且最小样本例数大于5或g＞3时
  • 多样本区组设计比较秩和检验
    • Friedman M 检验
      • 确定P值
        • 查表法
          • 当n≤5和g≤15时，查M界值表
        • X²分布近似法
          • n、g超出M界值表范围时
  • 等级资料的比较
    • 两样本比较
    • 多组等级资料比较
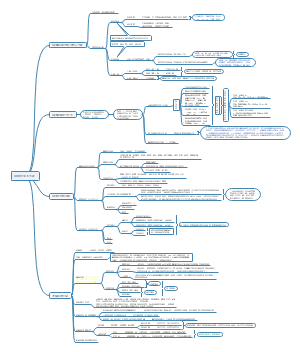
• 统计图和统计表
  • 统计表
    • 基本要求
      • 1.标题:放在表上方
      • 2.标目:要有横标目、纵标目，注意单位
      • 3.线条:至少用三条线，只有横线
      • 4.数字:无数字用“-”表示，缺失数字用“…”表示， 数值为0者记为“0”，不要留空项，数字按小数位对齐
      • 5.备注:标“*”号，在表下方说明
    • 种类
      • 简单表:主语只有一个层次
      • 组合表:主语有两个以上层次
  • 统计图
    • 基本要求
      • 1.正确选用适当统计图
      • 2.标题:位于图下方
      • 3.横纵轴注明标目单位
      • 4.图例:不同颜色或线条表示，放在图的右上角或下方位置
    • 常用统计图
      • 直条图
        • 相互独立资料
        • 纵轴起点从零开始
        • 用直条长短表达数值大小
      • 直方图
        • 连续性变量的频数表资料
        • 横轴组距相等
        • 用矩形面积表达各组段的频数或频率
      • 圆图
        • 构成比资料
        • 圆的总面积为100%
        • 用圆的扇形面积表达内部构成比
      • 百分比条图
        • 构成比资料
        • 圆的总长度为100%
        • 用直条各段的长度表达内部构成比
      • 线图
        • 连续性资料
        • 纵轴为算术尺度
        • 用线段的升降表达事物的动态变化
      • 半对数线图
        • 连续性资料
        • 纵轴尺度为对数
        • 用线段的升降表达事物的发展速度
      • 散点图
        • 双变量资料
        • 变量x为横轴变量，y为纵轴
        • 用点的密集度和趋势表达两变量间的相关关系
      • 箱式图
        • 计量资料
        • 均数最大值，均数最小值，中位数，25%、75%的百分位数
        • 用典型值比较数据的内部特征
      • 统计地图
        • 区域性资料
        • 在地图上标识
        • 描述区域性特征
• 直线回归与相关
  • 线性回归
    • 概述
      • 简单线性回归
      • 基本步骤
        • 1.绘制散点图
        • 2.估计回归参数，列出回归方程
        • 3.对回归方程进行假设检验
        • 4.在散点图上绘制回归直线
        • 5.解释回归系数的统计学意义
        • 6.评价回归方程的拟合效果
          • 剩余标准差
          • 决定系数r²=SS回归/SS总 r²越大（越接近1），拟合效果越好
    • 应用
      • 条件
        • 线性
        • 独立
        • 正态性
        • 方差齐
      • 区间估计
        • 总体回归系数β可信区间估计
        • 个体Y的预测值容许区间估计
    • 残差分析
      • 评价资料是否符合回归分析的条件
      • 识别异常点
      • 了解资料和回归模型之间的关系
  • 线性相关
    • 相关关系与确定性关系
      • 确定性关系:两变量间的函数关系
      • 非确定性关系:在宏观上存在关系，但未精确到可以用函数关系表达
      • 相关关系:相关关系不一定是因果关系
    • 两定量资料的相关
      • 分析步骤
        • 散点图
        • 相关系数计算
          • 总体相关系数ρ（－1≤r≤1）
        • 相关系数的假设检验
          • H0:ρ=0，……无相关关系
          • H1:ρ≠0,……有相关关系
    • 秩相关
      • Spearman等级相关
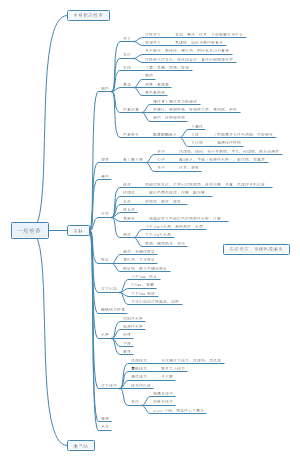
• 小总结
  • 资料类型
    • 定量资料
      • 正态，方差齐
        • 单组设计
          • 样本与总体均数比较的t检验
        • 完全随机设计
          • 多组
            • 单因素方差分析
          • 两组
            • 两样本的t检验
        • 配对设计
          • 两组
            • 配对t检验
          • 多组
            • 随机区组设计方差分析
      • 非正态，方差不齐
        • 单组设计
          • Wilcoxon符号秩和检验
        • 完全随机设计
          • 两组
            • t'检验、Wilcoxon秩和检验
          • 多组
            • Kruskal–Wallis H秩和检验
        • 配对设计
          • 两组
            • Wilcoxon符号秩和检验
          • 多组
            • Friedman M 秩和检验
    • 定性资料
      • 无序
        • 单组设计
          • 二项分布直接计算概率法、正态近似法(Z检验)
        • 完全随机设计
          • 两组
            • X²检验，确切概率法
          • 多组
            • R×C表资料X²检验、确切概率法
        • 配对设计
          • 两组
            • 配对四格表X²检验。
          • 多组
            • R×C列联表配对X²检验
      • 有序
        • 完全随机设计
          • 两组
            • Wilcoxon秩和检验
          • 多组
            • Kruskal–Wallis H秩和检验
        • 配对设计
          • 两组
            • Wilcoxon符号秩和检验
          • 多组
            • R×C列联表配对X²检验
• 对于行×列表多个样本率/构成比比较的X²检验， 不能有1/5以上的格子理论数少小于5或者 不能有一个格子的理论数小于1， 否则易出现偏性。
• 有统计学意义后进行两两比较 方法:SNK、Dunnett、LSD