导图社区 期货及衍生品分析与应用 第3章 分析方法
期货及衍生品分析与应用 第3章 分析方法
这是一篇关于私募基金的全景图（上）的思维导图，对于私募基金不知道大家的了解有多少，本图提供大家一个思路分析。
结构化产品是以金融工程学知识为基础，利用基础金融工具和金融衍生工具进行不同的组合得到的一类金融创新产品。最为流行的结构化金融衍生品主要是由商业银行开发的各类结构化理财产品以及在交易所市场上可上市交易的各类结构化票据，它们通常与某种金融价格相联系，其投资收益随该价格的变化而变化。
金融期货及衍生品是指以金融工具为标的物的期货合约或期权等衍生产品。权益类、利率类和汇率类衍生品三大类。
社区模板帮助中心，点此进入>>
费用结算流程
租赁费仓储费结算
E其它费用
F1开票注意事项
F2结算费用特别注意事项
洛嘉基地文件存档管理类目
CFA一级Ethics-standard思维导图
货币政策对黄金价格的传导机制
云报税（个税）
收入
第3章 分析方法
基本分析方法
概念
方向性判断
价格及其运动和变动趋势
期货品种、期货板块也包括对期货相关指数和宏观经济指标
解决
期货价格的运动方向问题，即趋势问题
经济周期分析法
经济周期及其对期货市场的影响
周期性的波动
繁荣
经济活动扩张或向上阶段
衰退
由繁荣转为萧条的过程，经济活动的收缩或向下阶段
萧条
经济活动的收缩或向下阶段
复苏
由萧条转为繁荣的过渡阶段
期货价格影响
经济运行周期
最重要的因素
决定
变动趋势
宏观经济
良好
投资和消费增加，需求增加
价格攀升
恶化
投资和消费减少，需求下降
价格下滑
大类资产配置应用
美林投资时钟
衰退阶段（6～9点）
产能过剩
盈利能力下降
去库存
价格下行
低通胀甚至通缩
复苏阶段（9～12点）
经济开始增长
过剩产能还没消化
通胀较低
过热阶段（12～3点）
经济持续加速增长
产能增加
通胀高
滞涨阶段（3～6点）
经济增长降到合理水平下
通胀仍继续
成本上升挤压利润空间
明斯基时刻
资产价值崩溃的时刻
经济长时期稳定
导致债务增加、杠杆比率上升
金融危机和陷入漫长去杠杆化 周期
特点
优点
长期性、趋势性较好
长期趋势分析较有帮助
国债、股市以及金融属性强
缺点
周期判断正确
不应忽略短期、中期
幅度不小的波动
影响因素的复杂化
不可过分迷信
平衡表法
作用
说明
供求关系
平衡表构成
期末结转库存，当期生产量，进口量，消耗量，出口量，当期结转库存等
前期对照值、未来预测值
公式
期初库存=上期末库存
期末库存=总供应量-总使用量
库存消费比=期末库存/总使用量（包括国内消费和出口）
其他
产量=收获面积（不是播种面积）×平均单产
总供应量=期初库存+产量+进口量
总使用量=压榨量+出口量+种子用量+残余用量
国内消费=总使用量-出口量
简单明了，部分数据公开、透明、容易取得
综合考虑
巨大影响
社会库存、走私量等信息
不同机构
统计口径不同
季节性分析法
较适合
原油和农产品
因季节变动产生规律性变化
供应淡季或者消费旺季
价格高企
供应旺季或者消费淡季
价格低迷
容易掌握，简单明了
只适用特定阶段
结合其它阶段性因素客观评估
特殊情况
供求失衡
削弱原油季节性规律
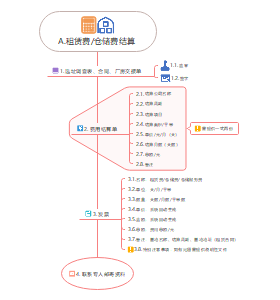
成本利润分析法
价格区间判断
底部或顶部
重要参考指标
期货产品生产成本线或企业盈亏线
成本利润分析
不能单独计算某一商品
考虑上下游、副产品价格、替代品价格和时间等因素
大豆及其相关产品利润分析
种植成本与利润
国产大豆现货
较强的成本支撑
进口成本
到岸价格（美元／吨）=[CBOT（芝加哥期货交易所）期货价格（美分/蒲式耳）+到岸升贴水（美分/蒲式耳）]*0.36475（美分／蒲式耳转换成美元／吨的换算率）
到岸完税价（元／吨）＝到岸价格（美元／吨）＊1.13（增值税）＊1.03（关税）＊美元对人民币汇率＋港杂费
未来进口的大豆成本
判断
套期保值
期货盘面出现压榨利润
盘面卖出压力可能开始增加
大豆压榨利润及期货套期保值利润
油厂大豆现货压榨利润＝豆粕出厂价＊出粕率＋豆油出厂价＊出油率－进口大豆成本－压榨费用
大豆期货盘面套期保值利润＝豆粕期价＊出粕率＋豆油期价＊出油率－进口大豆成本－压榨费用
注意
结果是动态价格
与现时点有差异
产生副产品或者可循环利用的产品
科学性、参考价值较高
价格
易受供求关系、资金炒作等影响
结合
其他基本面分析
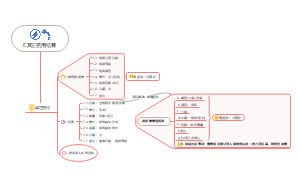
持仓分析法
研究
持仓内部结构
各会员
多空持仓变化
分析
买卖双方力量变化
预测
方向
主力机构的持仓方向
影响
国内
最前20名会员额度单位及数量
当日交易量和多空持仓量
方法1
多空主要持仓量
多空合计数之差
多>空
多单在主力，空单在散户
反之亦然
方法2
寻找主力所在
多单（空单）是否集中
结合价格涨跌找主力
即“区域“或“派系”
方法3
某一品种
主要席位
交易状况和持仓增减
美国CFTC持仓报告分析
概述
收集期货持仓构成数据
美国商品交易委员会（ＣＦＴＣ）
权力部门
监管期货和期权交易、促使市场免于虚假价格
一部分
公布
美国商品交易委员会的持仓报告（COT）
持仓分类
报告交易商持仓
头寸超过水平
美国商品交易委员会规定
基金持仓
一般来自期货或者商品基金
商业持仓
生产商、贸易商、加工企业、用户
从事与现货有关交易
保值者
非商业持仓
互换交易商、资产管理机构、其他投资者
不涉及现货交易
投机者
CFTC报告中
最核心内容
意义
分析表现
大型对冲机构和大型投机商
预测价格
较好
对冲机构
预测效果
一贯好于
大型投机商
不同市场
结果差异较大
小型交易商
最差
商业头寸
净头寸的变化
不是持有多\空头
季节性变化
农产品
商业交易者
套期保值盘
资金面角度
短期作用明显
长期走势需结合其他
事件驱动分析法
系统性因素事件
宏观经济政策
货币政策、财政政策或者其他突发性政策等
金融衍生产品
价格变动
主要原因
包括
黑天鹅
意外性
产生重大影响
或多或少的可解释和可预测
与灰犀牛
相互补足
极其罕见的、出乎人们意料
灰犀牛
太过于常见以至于人们都习以为常
较典型
影子银行、房地产泡沫、国有企业高杠杆、地方债务、违法违规集资等
对商品期货的影响
估值
影响价格大趋势
如
货币政策宽松
提高估值
非系统性因素事件
微观层面的时间
影响具体某个品种
突发性事件
投资者面临
供需层面
主要比较
结果和预期
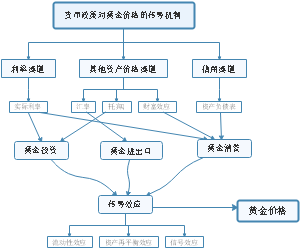
战争对黄金价格影响
事实之前
预期
主宰价格波动
局部性战争
影响局限在一定范围内
战争的溢价
持续时间不长
突发性越高
影响越高
不确定性越大
影响越大
战争出现
主权信用货币
持续贬值
黄金
升值开始
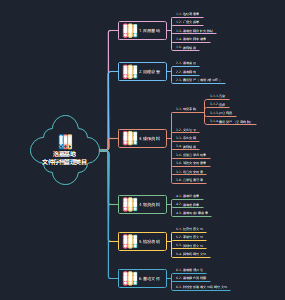
计量分析方法
相关关系分析
变量关系分类
确定性函数关系
变量
对应的确定关系
相关关系
变量取值
不能由另外一个变量唯一确定
x取?
y对应不是确定值
y对应某一种分布
没有关系
不相关
分析相关关系方法
观察
散点图
变量之间
求解
相关系数的大小
度量相关程度
变量之间线性关系
相关系数
分类
总体相关系数
计算
总体全部数据
样本相关系数r
样本数据
取值范围
-1≤r≤1
取值意义
|r|越接近于1
相关关系越强
|r|越接近于0
相关关系越弱
r大于0
正向相关
r小于0
负向相关
r等于0
不存在线性关系
不表示没有关系
线性回归分析
一元
基本假定
i=1，2，3，……，n
yi：因变量或被解释变量
xi：自变量或解释变量
μi：一个随机变量，随机扰动项
满足
假定1
μi（i=1，2，3，……n）均独立同分布
正态分布随机变量
E（μi）=0
=常数
假定2
每个μi
不互相关
Cov（μi，μj）=0（i≠j）
假定3
μi与自变量任一观察值xi
Cov（μi，xi）=0（i=1，2，3，……n）
α、β：常数，回归参数
步骤
模型设定
求相关系数
建立回归模型
参数估计
最小二乘法
拟合最优
回归残差
yi观察值
回归值
：α、β估计量
使残差平方和最小
普通最小二乘法
ei：μ估计量
模型汇总
查表
Anovaa
回归平方和➗总计平方和=
Df=n-2
系数a
常量B=α
xB=β
常量标准误差Se=
x标准误差Se=
常量t=t（）
xt=t（）
Sig与α对比
小于α
决绝原假设
模型检验
拟合优度
可决系数
TSS：总离差平方和
ESS：回归平方和
RSS：残差平方和
：总离差
：残差
：回归离差
TSS= ESS +RSS
TSS一定时
拟合优度越大
线性回归效果越好
接近1
效果越好
接近0
效果越差
T检验
回归系数检验
提出假设
原假设H0：β=0
备择假设H1：β≠0
构造t统计量
服从自由度n-2的t分布
给定显著水平α
查n-2的t分布
得
拒绝原假设H0：β=0
接受备择假设H1：β≠0
x对y产生显著影响
x对y影响不显著
模型应用
y如何随x变化
点预测
i推某个预测值f
已知xf得yf，看作E（yf）
区间预测
置信度1-α
y平均值区间预测
预测期平均值
：残差平方和
y个别值区间预测
y的真实值yf
特征
同置信程度
个别值区间宽
个别值误差大
样本n越大
越精确
xf离x均值越近
越大
抽样范围越宽
多元
关系
一个因变量
多个自变量
零均值
E（μi）=0（i=1，2，……n）
同方差与无自相关
Var（μi）==常数（i=1，2，……n）
无多重共线性
无线性关系
解释变量间
互不相关
解释变量与随机扰动项
Cov（μi，μji）=0（i=1，2，……n，j=1，2，……k）
正态性
正态分布
随机扰动项
μi~N（0，）
最小二乘准则
最小
βj（j=0，1……k）的估计值
F
Sig.<0.05
5%显著性水平下拒绝原假设
其他B=β1，β2……
其他标准误差Se=1，2……
其他t=t（1）……
多个Sig.<0.05
检验
变大
随解释变量增多
修正可决系数
n：样本容量
k：解释变量个数
可能变小、负值
显著性F检验
原假设H0：β1=β2=……=βk=0
备择假设H1：βj（j=0，1，……k）不全为0
构造F统计量
服从自由度n-k-1的F分布
查自由度n-k-1的F分布
得Fα（k，n-k-1）
F>Fα（k，n-k-1）
拒绝原假设H0：β1=β2=……=βk=0
接受备择假设H1：βj（j=0，1，……k）不全为0
线性关系显著
影响不显著
备择假设H1：βj≠0（j=0，1，……k）
服从自由度n-k-1的t分布
查n-k-1的t分布
接受备择假设H1：βj≠0（j=0，1，……k）
xj对y产生显著影响
xj对y影响不显著
如何只随一个条件变化
时间序列分析
预测未来值
根据
某个变量的过去值
基本概念
随机过程
集合
按时间顺序排列
随机变量Y
连续型随机变量
Y（t）
离散型随机变量
Yt
平稳性随机过程
均值和方差不随时间改变
任两期协方差值
仅依赖于两期距离或滞后长度
不依赖于事件
反之
非平稳随机过程
白噪声过程
均值0
方差
不变常数
序列
无相关性
自相关函数与偏自相关函数
自相关函数ρ
时间序列Yt
ρk=
平稳时间序列
有
偏自相关函数φ
yt和
k=1
φkk=ρ1
k>1
平稳和非平稳时间序列
随着时间的变化
不变化
均值、方差和协方差
非平稳时间序列
不是平稳时间序列
单整
d阶单整序列yt_I(d)
非平稳序列{yt}
d次差分成平稳序列
d-1次差分不平稳
例
1，3，7，13，21
1次差分
2，4，6，8
0阶单整序列yt_I(0)
序列{yt}本身平稳
1，2，3，4
非平稳序列转化为平稳序列
差分平稳过程
时间序列
1阶单整
趋势平稳过程
趋势线上平稳
将其对时间做回归
回归后残差项平稳
残差项估值
是平稳时间序列
非平稳序列的单位根检验
DF检验
三种线性回归模型
无漂移项，无趋势项
有漂移项
无趋势项
有趋势项
t=1，2……T；μt~i.i.d.N(0,)
若γ=1
有单位根
非平稳序列
原假设H0：γ=1
拒绝原假设
无单位根
平稳性时间序列
不拒绝原假设
操作
方程双方减去
λ=γ-1
原假设变成H0：λ=0
最小二乘法估计值
服从DF分布
1%、5%、10%显著性下比较t和DF是否拒绝原假设
ADF检验
DF存在问题
1阶滞后相关才有效
大多数
高级滞后相关
三种模型
原假设H0：λ=0
ARMA模型
自回归移动平均模型
因变量回归得到
对因变量对的滞后值
对随机误差项的现值和滞后值
细分
移动平均（MA）
c常数项
{ε}白噪音果诚
引入之后算子L
自回归（AR）
{v}白噪音果诚
AR（p）
平稳条件
的根
全在单位圆之外
过程特征
无条件期望相等
设为u
自回归移动平均（ARMA）
ARMA（p,q）过程平稳性条件
应用
识别
核心工具
自相关函数（简记为ACF）
偏自相关函数（简记为PACF）
及它们各自的相关图
MA、AR、ARMA果诚自相关函数及偏自相关函数的特点
MA（q）过程的ACF特征
若j>q
ACF（j）=0
截尾
AR（p）过程的PACF的P阶截尾
当j<P
PACF取值不为0
当j>P
PACF取值为0
AR（P）过程的ACF以及MA（q）过程的PACF特征
平稳的AR（p）过程可转化为MA（∞）过程
AR（p）过程的ACF是拖尾
可逆的MA（q）过程可转化为AR（∞）过程
MA（q）过程PACF是拖尾
判断平稳性
ACF和PACF
确定ARMA（p，q）中p、q可能值
ACF、PACF以及它们的图形
诊断与检验
检验参数估计值
是否具有统计显著性
t统计量
检验残差序列
随机性
博克斯-皮尔斯（Box-Pierce）提出的Q统计量
原假设H0：p1=p2=……pk（模型误差序列是白噪声过程）
自相关系数估计值
用残差序列计算
若拟合不正确
序列有其他成分
Q将很大
拟合正确
Q值很小
判别
若
不拒绝H0
拒绝H0
协整分析和误差修正模型
协整
多个非平稳性时间序列
某种线性组合平稳
{xt}和{Yt}均为一阶单整
即xt~I（1）,yt~I（1）
一组非零常数α0和α1
使得α0 xt+ α1 yt~I（0）
E-G两步法
原理
设xt，yt
xt~I（1），yt~I（1）
协整模型
yt=α0+α1xt+ut
最小二乘法估得估计年纪残差序列
平稳
存在协整
误差修正模型
基本思想
变量间存在协整
存在着长期均衡关系
实现过程
短期波动过程中的不断调整
GARCH类模型分析
波动率
衡量
用资产收益率的条件方差
条件方差越大
风险越高
聚集现象
价格剧烈波动期后
还是
跟随者价格剧烈波动期
价格波动较平缓期后
价格波动平缓期
交替出现
明显杠杆效应（非对称性）
正负收益率
对未来波动率影响不对称
一般负影响很大
持续性
慢慢消减
随时间
直至消失
金融资产收益率
尖峰厚尾、波动率聚集
ARCH回归条件异方差波动率模型
Engle提出
20世纪70年代后
波动率随时间变化
线性依赖过去收益率
聚集性
金融数据
尖峰厚尾
GARCH广义回归条件异方差波动率模型
Bollersley提出
局限性
非负线性约束条件（参数非负）
估计模型参数
被违背
杠杆效应
收益率
无法解释
没有建立联系
当期条件异方差与条件均值
延伸
GJR或TGARCH模型
增加虚拟变量I
前期收益率为负
当期的I值取1
前期收益率非负
当期的I值取0
收益率存在杠杆效应
参数γ显著不为0
EGARCH模型
解决波动率杠杆效应
α2≠0
杠杆效应存在
解决非负线性约束条件违背
条件异方差取对数处理
MGARCH模型（GARCH-in -Mean模型）
建立关系
条件异方差与条件均值
γ的系数显著不为0
当期资产收益率
受影响
前一期资产波动率
