统计推断复习

医学统计学推断部分复习总结，"统计推断的核心：从数据中挖掘真相！本文系统梳理统计推断要点，涵盖参数估计（可信区间计算、中心极限定理应用）、假设检验（z检验、两类错误控制）和方差分析（变异分解思想）重点解析：①置信区间与医学参考值范围的区别②标准差与标准误的异同③多重比较替代t检验的原因④不同设计类型的变异分解附统计描述技巧（频数表、直方图绘制）和资料类型处理（计量/计数/等级资料），助你掌握数据分析底层逻辑。

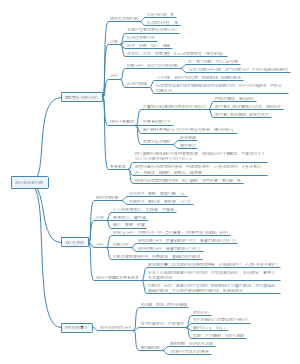
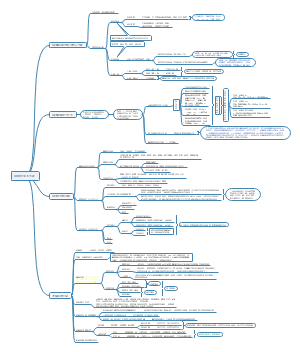
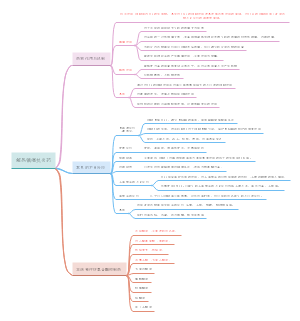
统计推断复习

• 参数估计
  • 抽样误差
    • 由于抽样造成的样本量与总体参数之间的差异
  • 均数标准误
    • 反应样本均数之间的变异，即反映抽样误差的大小
      • 样本均数服从正态分布的情况
        • 从正态分布的整体中抽样
        • 样本量大（>=50），根据中心极限定理样本均数都近似服从正态分布
    • 标准差和标准误的区别
      • 标准差
        • 反映个体观察值之间的变异
      • 标准误
        • 反映样本均数之间的变异，可以反映抽样误差大小
  • 率的标准误
    • 样本率的标准差
  • 可信区间
    • 区间估计
      • 按照事先给定的概率进行参数估计得到的区间
    • 可信度
      • 事先给定的概率1-α
    • 又被称为置信区间CI
      • 意义：该区间包括总体均数μ的概率
    • 估计效果
      • 准确度
        • 可信度1-α
      • 精确度
        • 区间的宽度
      • 两者相互矛盾，但在可信度确定的情况下，增大样本量可减小区间宽度
    • 按照给定的可信度计算得出包含未知总体参数的区间
  • 总体均数的区间估计
    • σ已知
      • 样本均数服从标准正态分布z
    • σ未知
      • 统计量服从t分布
      • 如果样本大于50，样本均数也服从z分布
  • 两总体均数差值的区间估计
    • 简单记一下公式（草稿）
• 假设检验
  • 基本原理
    • 显著性检验
    • 目的
      • 定性比较总体参数之间有无差别或总体分布是否相同
    • 基本思想
      • 根据现有样本计算统计量，得到P值，如果P值很小，根据小概率事件不可能在一次事件中发生的原理，倾向于拒绝H0，接受H1,认为两样本之间的差异有统计学意义
  • 两类错误
    • I类错误
      • 错误地拒绝了H0，实际情况与H0一致
      • 概率
        • α
    • II类错误
      • 错误地接受H0，实际情况为拒绝H0
      • 概率
        • β
          • 难以估计
    • 两者概率趋势相反，想要同时减小α、β只能增加样本量
  • 检验效能
    • power of test
      • 当不同的总体间确有差别时，按检验水准α能发现差别的能力，用1-β
  • 假设检验选择
    • 计量资料
      • 单组比较
        • 正态性
          • 单样本t检验（比较均数）
      • 两组比较
        • 配对设计
          • 正态
            • 配对t检验（比较差值d是否为0）
          • 非正态
            • Wilcoxon符号秩和检验
        • 完全随机设计
          • 正态，方差齐
            • 两独立样本均数比较的t检验
          • 正态，方差不齐
            • t'检验
          • 非正态，方差不齐
            • Wilcoxon秩和检验
          • 大样本可使用z检验
            • 依据：中心极限定理
        • 方差齐性检验
          • 方差分析
      • 多组比较
        • 随机区组设计
          • 正态，方差齐
            • 随机区组设计的方差分析
          • 非正态或方差不齐
            • Friedmen秩和检验
        • 完全随机设计
          • 正态，方差齐
            • 完全随机设计的方差分析
          • 非正态或方差不齐
            • H检验（H-W检验）
        • 多个样本均数的两两比较
          • 不能使用t检验
            • 极大增加了犯I类错误的概率
          • 比较方法
            • LSD-t检验
              • 一对或几对在专业上有特殊意义的样本均数间的比较，理论上只适合两组之间
            • SNK-q检验
              • 多个样本两两之间全面比较
            • Dunnett-t检验
              • 多个实验组与对照组之间比较
        • 方差齐性检验
          • 正态分布
            • Bartlett检验
          • 非正态分布
            • Levene检验
        • 注：随机区组设计是配对设计的拓展
    • 计数资料
      • 两组比较
        • 配对设计
          • McNemar假设检验法
            • b+c>=40
            • b+c<40
        • 完全随机设计
          • n>=40且所有T>=5
            • 不校正，卡方检验
          • n>=40且1=<T<5
            • 连续性校正卡方检验
          • n<40或T<1
            • Fisher确切概率法
      • 多组比较
        • 卡方检验
        • Fisher确切概率法
          • T<1或1<T<=5超过格子总数1/5
    • 等级资料
      • 单组比较
        • Wilcoxon符号秩和检验
          • 目的
            • 比较未知样本中位数和已知总体中位数是否相同
      • 两组比较
        • 配对设计
          • Wilcoxon符号秩和检验
            • 基本思想
              • 推断配对资料差值是否来自中位数为0的总体
              • 假定两种处理效应相同，则差值的总体分布对称，总体中位数为0，即样本正负秩和绝对值相近
            • 目的
              • 比较差值中位数和0的差别
        • 完全随机设计
          • Wilcoxon秩和检验
            • 目的
              • 比较两总体分布位置有无差异
            • 确定秩和检验统计量T
              • 编秩次
              • 分别求两组的秩和
              • 统计量T的确定
                • 例数相同取n较小的为统计量
            • 确定P值
              • n1<=10,n2-n1<=10，查表
              • 上述条件任意不满足，正态近似检验
              • 相同秩次较多采用校正公式
      • 多组比较
        • 随机区组设计
          • Friedmen秩和检验
        • 完全随机设计
          • H检验
            • 组数k=3,且每组例数<=5，查H界值表
            • k>3或每组例数>5时，H近似服从自由度为k-1的卡方分布
  • 假设检验步骤
    • 建立假设检验，确定检验水准
      • H0：μ1=μ2，+专业结论（...相同）
      • H1：μ1≠μ，+专业结论（...不相同）
      • 其他
        • 注意比较的对象
        • 多个均数的比较→多个均数之间不全相等（方差分析）
        • 率的比较π1=π2（卡方检验）
        • 秩和检验
          • 比较的是总体分布的位置
            • 结论中写清楚总体分布位置（相同、不相同、不全相同）
        • 线性回归
          • β=0
        • 线性相关
          • ρ=0
        • 多元线性回归
          • H0：β1=β2=..βm=0
          • H1：β1..βm之间至少有一个不为0
        • logistic回归
          • βj=0
        • Cox回归
          • βj
        • log-rank检验
          • S1（t）=S2（t）
    • 计算检验统计量
      • 根检验类型有关
      • 注意自由度计算
  • 秩和检验注意事项
    • 特点
      • 非参数估计
    • 应用
      • 有序分类资料（等级资料）
      • 分布类型未知的资料（不服从正态分布）
      • 开口资料
      • 不符合参数检验条件的资料
    • 推断目的
      • 比较一个总体表达分布位置的中位数和已知中位数是否有差别
      • 推断两个或多个总体的分布位置是否有差别
    • 编秩次
      • 省略所有为0的对子数，相应样本总数减去为0的对子数
      • 按差值的绝对值编秩次，绝对值相等取秩次的平均值，最后加上正负号
      • 求正秩和和负秩和，任取一个作为检验统计量
    • 确定P值
      • n<=50
        • 查表，在范围内则P>该范围对应的概率
        • 不在范围内则小于范围对应的概率
      • n>50
        • 近似正态法，相同秩次太多则用校正后的近似正态公式
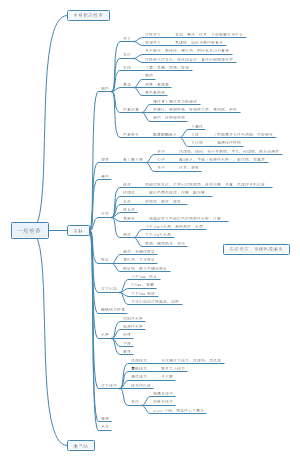
• 统计描述
  • 定量资料的统计描述
    • 频数表
    • 直方图
      • 描述数据的分布特征和形态
        • 对称分布
        • 偏态分布
          • 正偏态分布
          • 负偏态分布
    • 用途
      • 陈述资料的形式，代替原始资料做进一步分析
      • 观察数据的分布类型
      • 发现离群值和异常值
      • 样本量较大时可用频率代替概率
    • 集中趋势的描述指标
    • 离散趋势的描述指标
  • 定性资料的统计描述
    • 常用相对数
      • 率
        • 在一定空间或时间范围内某现象的发生数与可能发生的总数之比
        • 意义
          • 表示某现象出现的强度或频率
        • 特点
          • 强调时间范围，指某一段时间内某现象发生的强度或频率
      • 构成比
        • 某事物内部各组成部分在整体中所占的比重
        • 特点
          • 构成比之和为100%
          • 内部为此消彼长的关系
        • 注意
          • 不能用构成比代替率
            • 意义不同
              • 率反映某事物发生的强度或频率
              • 构成比反映某组成部分在整体的比重
            • 构成比内部此消彼长，率不会随其他率的改变而改变
            • 死亡构成比仅能反映某病死人数在总病死人数的比重，不能反映疾病的严重程度，因用病死率表示
          • 平均率不等于率的平均
          • 构成比和率的比较应做假设检验（存在抽样误差），同时要注意可比性
      • 相对比
        • 例数比
          • 倍数关系
        • 相对危险度
          • 两种不同条件下疾病发生的概率之比
          • 意义
            • 反映疾病和暴露之间的关联强度
        • 比数比
          • 又称优势比，指病例组和对照组中暴露和非暴露比例之比
          • 意义
            • 反映疾病和暴露之间的关联强度
      • 标准化率
        • 在比较两不同人群的患病率、发病率和死亡率等资料时，为消除其内部构成（年龄、性别、工龄、病情轻重等）对率的影响，可以使用标准化率
        • 计算方法
          • 直接法
            • 计算公式（见草稿）
            • 标准构成选取
              • 选取有代表性、较稳定、数量较大的人群作为标准构成，如全国或全身范围内的数据
              • 选取各组例数合计
              • 从需要比较的组中仍选一组
        • 注意事项
          • 仅反映相互比较的各组间的相对水平，不反映实际情况，选用的标准不同得到的标准化率可能不同
    • 医学中常用的相对数
      • 死亡统计指标
        • 死亡率
          • 某年某地每千人口中的死亡人数，反映当地居民总的死亡水平
        • 年龄别死亡率
          • 某年某地在某年龄组中每千人口的死亡人数
          • 消除了年龄构成不同对死亡率的影响
        • 死因别死亡率
          • 某年某地每10万人口中因某原因的死亡人数
          • 反映各类病伤死亡对居民生命的伤害程度
        • 死亡构成比
          • 全部死亡人数中，死于某死因的人数占总死亡数的百分比
          • 反映不同死因的相对重要性
      • 疾病统计指标
        • 发病率
          • 某时期内某病新发病例出现的频率
          • 反映疾病对人群健康影响和描述疾病分布状态的指标
            • 仅指这段时间内新患病的频率
        • 患病率
          • 某一时间点某人群患某病的频率
          • 表示病程较长的慢性病的发生或流行情况
        • 发病率和患病率的区别
          • 意义
            • 一个指某时期内新发病的频率，一个指某时间内所有患病人数的频率
            • 发病率
              • 反映某疾病对人群健康影响及疾病分布状态
            • 患病率
              • 反映慢性病的发生或流行情况
          • 分子
            • 某时间的新发病例
            • 某时间内所有患病人数
          • 分母
            • 可能会发生该病的人群，不包括已患病和打疫苗的人群
            • 所有调查人数
        • 病死率
          • 某时期内某病患者中因该病死亡的频率
          • 表示该病的严重程度和医疗水平，多用于急性传染病
          • 分母为同期患有该病的人群
            • 与死因别死亡率的区别
              • 定义
              • 意义
              • 区别
                • 死因别死亡率
                  • 分母为某时期内当地平均人口数
                • 病死率
                  • 分母为某时期内患者数
        • 治愈率
  • 统计表和统计图
    • 统计表
      • 统计表的编制原则
        • 重点突出，简洁明了
          • 一张表只表达一个中心内容和主题
        • 主谓分明，层次清楚
          • 主语在左边作为横标目
          • 谓语在右边作为纵标目
        • 格式规范
          • 数据规范，文字和线条从简
      • 统计表的结构
        • 标题
          • 正中上方，包括时间、地点和内容，多张表格要编号，度量衡一致放在后面括号内
        • 标目
          • 总标目是对纵标目的归纳
          • 层级不宜多于三个
        • 线条
          • 一般为三线表
        • 数字
          • 阿拉伯数字，位数对齐，小数位数一致
            • 不留空格
              • 无数字-
              • 缺失...
              • 数字零0
        • 备注
    • 统计图
      • 统计图的编制原则
      • 统计图的结构
        • 标题
          • 位于图的正下方，包括时间地方和内容，有编号
        • 图域
          • 原图，直角坐标系第一象限，长方形框架
        • 标目
          • 纵轴和横轴数字刻度意义，有单位要标出
        • 图例
          • 不同颜色或图案的注释，通常放在图域和标题之间
        • 刻度
          • 表示量值大小的记号
      • 描述定量资料的统计图
        • 直方图
          • 描述连续性变量频数分布情况
          • 注意事项
            • 纵轴从0开始
            • 各矩形的高度为频数或频率，宽度为组距
        • 线图
          • 通过线段的上升或下降表示指标的连续变化过程，适用于描述一个指标随着另一个指标变化的趋势和波动情况
          • 分类
            • 普通线图
            • 半对数线图
              • 纵坐标为对数尺度，反映研究指标变化的速度
        • 箱式图
          • 比较两组或多组数据的平均水平和变异程度，可体现中位数、四分位数间距、最大值和最小值，适合于偏态分布
        • 误差条图
          • 表示多组资料比较的均数和标准差（或标准误、可信区间）
        • 散点图
          • 用点的密集程度和变化趋势表示两指标之间的直线或曲线关系
      • 描述定性资料的统计图
        • 直条图
          • 等宽直条表示相互独立的统计量数值大小
        • 构成图
          • 圆图
          • 百分条图
  • 医学参考值范围
    • 均数的可信区间和医学参考值范围的区别
    • 制定医学参考值范围的注意事项
      • 确定同质的参照总体
        • 正常人
          • 符合特定健康水平的人
      • 确定足够例数的参照样本
      • 控制检测误差
        • 控制随机误差，避免系统误差和过失误差
      • 选择单双侧界值
        • 根据专业知识确定
      • 选择适当的百分数范围
        • 一般为95%
          • 根据研究目的可适当缩小或增大
• 问答题
  • 标准差和标准误的区别
  • 方差分析基本思想及应用条件
    • P28
  • 置信区间和医学参考值范围的区别
    • P19
  • 方差分析中完全随机设计和随机区组设计变异分解的区别
  • 变异分解思想
  • 为什么用多重比较不用两两t检验？
    • 增加I类错误概率