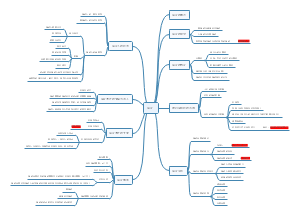
经济法-博弈思维导图

预测及解释行为，解决现实问题，研究合作和竞争的生活必备理论；博弈论是研究决策主体在决策主体之间的相互作用及影响主体决策效果的理论。

博弈

• 博弈论简介
  • 博弈论的定义
    • 1. 博弈论是研究决策主体在决策主体之间的相互作用及影响主体决策效果的理论。
    • 2. 博弈论是研究主体对主体决策行为的数学模型。
    • 3. 博弈论是研究主体对主体决策行为的数学理论。
    • 4. 博弈论是研究主体对主体决策行为的数学模型和理论。
  • 博弈论的应用领域
• 博弈类型
  • 零和博弈
    • 1. 零和博弈：指双方参与者中，一方获益将导致另一方损失，总和为零。
    • 2. 完全信息：在零和博弈中，所有参与者都了解所有相关信息。
    • 3. 策略空间：双方都有一定的策略选择空间，每种策略都有对应的收益。
    • 4. 最佳反应：对于任意给定的策略，参与者都会选择最佳反应以最大化自己的收益。
    • 5. 纳什均衡：在零和博弈中，如果每个参与者都选择了最佳反应，那么这种策略组合就是纳什均衡。
    • 6. 重复博弈：在零和博弈中，如果博弈是重复进行的，那么参与者的策略选择会影响未来的收益。
    • 7. 囚徒困境：零和博弈的一种经典案例，双方都选择“坦白”以最大化自己的收益，导致总体利益最小化。
    • 8. 实际应用：零和博弈在经济学、政治学、军事等领域都有广泛的应用。
  • 非零和博弈
    • 1. 非零和博弈是一种参与者能够同时获益的博弈类型。
    • 2. 在非零和博弈中，各方的利益并非相互排斥，而是可以同时实现。
    • 3. 合作是实现非零和博弈的关键，参与者通过合作能够实现更大的共同利益。
    • 4. 非零和博弈强调了双赢的可能性，让参与者有更大的动力寻求合作。
    • 5. 现实中很多经济、政治、军事等领域的问题都可以用非零和博弈来描述。
    • 6. 非零和博弈的理论研究对于理解和解决现实问题具有重要的指导意义。
    • 7. 在非零和博弈中，策略的选择和调整需要考虑到对方的反应和可能的合作。
    • 8. 非零和博弈的概念不仅适用于个体与个体之间的竞争，也适用于个体与集体、集体与集体之间的竞争。
  • 完全信息博弈
    • 1. 完全信息博弈中，参与者对所有信息都有全面了解。
    • 2. 纳什均衡是此类博弈的解，所有参与者都能做出最优决策。
    • 3. 零和博弈是一种完全信息博弈，一方的收益等于其他方的损失。
    • 4. 囚徒困境是经典的完全信息博弈问题。
    • 5. 重复剔除严格劣策略是求解完全信息博弈的方法之一。
    • 6. 完全信息动态博弈中，先行动者有信息优势，后行动者只能根据先行动者的选择做出反应。
    • 7. 完全信息博弈中，策略的帕累托有效是一种重要的均衡概念。
    • 8. 完全信息博弈广泛用于经济学、政治学、军事等领域的研究。
  • 不完全信息博弈
    • 1. 不完全信息博弈：参与者对其他参与者的策略空间、收益函数等信息不完全了解的博弈。
    • 2. 信息不对称：在不完全信息博弈中，各参与者的信息掌握程度存在差异。
    • 3. 贝叶斯纳什均衡：描述了在不完全信息博弈中，各参与者如何根据自身所掌握的信息选择最优策略的均衡概念。
    • 4. 信号传递：参与者通过一定的行为或信号传递信息，以影响其他参与者的决策。
    • 5. 信念修正：在接收到新的信息后，参与者会更新自己的信念，以更准确地反映博弈的现实情况。
    • 6. 混合策略：在不完全信息博弈中，参与者可能会采用混合策略，即以一定的概率选择不同的行动。
    • 7. 重复博弈：在多次进行的博弈中，参与者可能会考虑长远利益，而非单次博弈的收益，从而影响其策略选择。
• 博弈策略
  • 最优策略
    • 以下是围绕《博弈、博弈策略》输出“最优策略”的9个简短小点：
    • 1. 了解对手：在博弈中，了解对手的策略和偏好是制定最优策略的关键。
    • 2. 理性思考：博弈中需要保持理性，不被情绪左右，以便更好地制定和执行策略。
    • 3. 预测与应对：预测对手的行动并做出相应的应对是博弈策略的重要组成部分。
    • 4. 寻找均衡：在博弈中，寻找均衡策略可以使双方都达到满意的结果。
    • 5. 灵活变通：根据情况调整策略，保持灵活性是博弈中的关键。
    • 6. 长期视角：在制定策略时，需要考虑长期影响和结果，而不仅仅是短期收益。
    • 7. 合作与竞争：在博弈中，合作和竞争都是策略的一部分，需要权衡利弊。
    • 8. 优化决策：通过不断优化决策过程，可以提高博弈策略的有效性和准确性。
    • 9. 总结经验：在博弈结束后，及时总结经验教训，为下次博弈提供参考和改进方向。
  • 纳什均衡
    • 纳什均衡
      • 定义
        • 在一个博弈中，如果每个参与者的策略都是针对其他参与者的策略的最优反应，那么这个策略组合就是纳什均衡
      • 特点
        • 纳什均衡是博弈论中最重要的概念之一，它反映了参与者在博弈中的理性决策
        • 纳什均衡不一定是最优的，但它是参与者在给定条件下所能达到的最好结果
      • 例子
        • 囚徒困境
          • 两个囚徒被分开审讯，如果一方坦白而另一方不坦白，坦白的一方将获得减刑，不坦白的一方将受到重罚
          • 如果双方都坦白，他们都将受到较轻的处罚
          • 如果双方都不坦白，他们都将受到较轻的处罚
          • 在这个博弈中，纳什均衡是双方都坦白，但这并不是最优的结果
        • 智猪博弈
          • 在一个笼子里，一头大猪和一头小猪，笼子的一边有一个踏板，另一边有一个食槽
          • 如果大猪踩踏板，小猪就可以吃到食物，但如果小猪踩踏板，大猪就可以吃到食物
          • 在这个博弈中，纳什均衡是大猪踩踏板，小猪等待，但这并不是最优的结果
      • 应用
        • 纳什均衡在许多领域都有应用，包括经济学、政治学、社会学等
        • 纳什均衡可以帮助我们理解参与者在博弈中的行为，从而更好地制定策略和政策。
  • 混合策略
    • 1. 混合策略定义：混合策略是指在博弈中，参与者以一定的概率分布采取不同的行动。
    • 2. 概率分布：混合策略中的概率分布表示参与者采取每种行动的可能性。
    • 3. 纳什均衡：在混合策略的博弈中，如果每个参与者都以最佳混合策略应对其他参与者的混合策略，那么纳什均衡就是一种稳定的策略组合。
    • 4. 优势策略：在某些情况下，即使其他参与者采取混合策略，一个参与者也可能通过选择某个特定的优势策略来获得更高的收益。
    • 5. 风险占优：如果一个参与者采取混合策略以最大化其期望收益，并且该期望收益超过其他参与者可能获得的最高期望收益，那么该参与者的混合策略就被认为是风险占优的。
    • 6. 混合策略的复杂性：混合策略的复杂性在于参与者需要同时考虑其他参与者的可能行动和自己的可能反应，以确定最佳的混合策略。
    • 7. 混合策略的意义：混合策略在博弈论中具有重要的意义，因为它可以帮助我们理解在现实世界中如何制定复杂的决策和如何处理不确定性。
  • 重复博弈
    • 1. 重复博弈需要参与者长期互动，每次决策都影响未来的收益。
    • 2. 重复博弈可以促进合作，通过合作可以获得长期利益，而不是短期收益。
    • 3. 重复博弈需要参与者有耐心，能够抵制诱惑，做出正确的决策。
• 博弈分析方法
  • 静态博弈分析
    • 1. 博弈参与者：理解每个参与者的决策和目标，分析它们之间的互动关系。
    • 2. 策略空间：确定每个参与者的可选策略，以及这些策略可能带来的结果。
    • 3. 博弈均衡：寻找博弈中的均衡状态，即所有参与者最优策略的组合。
    • 4. 优势策略：分析每个参与者是否存在一个始终最优的策略，无论其他参与者如何选择。
    • 5. 博弈解：根据上述分析，确定博弈的解或解的概念，如纳什均衡、优势策略均衡等。
  • 动态博弈分析
    • 1. 动态博弈分析：研究博弈中的参与者如何根据对方的行动做出决策。
    • 2. 策略依赖性：参与者对对方策略的反应方式。
    • 3. 先行者优势：在动态博弈中，先行采取行动的参与者可能获得优势。
    • 4. 后行者策略：后采取行动的参与者根据先行者的策略来制定自己的策略。
    • 5. 子博弈精炼纳什均衡：在动态博弈中，子博弈精炼纳什均衡是更精确的均衡概念。
    • 6. 逆推归纳法：通过逆向推理找出子博弈精炼纳什均衡的方法。
    • 7. 完美信息博弈：参与者能够完全了解对方策略的动态博弈。
    • 8. 不完美信息博弈：参与者不完全了解对方策略的动态博弈。
    • 9. 扩展式博弈：将博弈表示为一系列行动和决策的序列，更全面地描述动态博弈过程。
  • 博弈树分析
    • 1. 博弈树分析是博弈论中常用的方法，通过构建博弈树来描述博弈双方的策略和结果。
    • 2. 博弈树可以帮助我们理解博弈的动态性和复杂性，展示双方的决策过程和结果。
    • 3. 博弈树分析可以揭示博弈中的优势和劣势，以及最优策略的选择。
    • 4. 通过博弈树分析，我们可以找到均衡策略和均衡结果，以及它们与初始条件的关系。
    • 5. 博弈树分析是一种直观和有效的工具，可以帮助我们更好地理解和解决各种博弈问题。
  • 矩阵博弈分析
    • 1. 矩阵博弈分析是一种通过矩阵形式表示参与者策略和收益的博弈分析方法。
    • 2. 矩阵博弈分析能够清晰地展示各参与者的决策和收益，便于分析博弈的均衡解。
    • 3. 矩阵博弈分析通常采用扩展型表示法，将参与者的决策和收益信息整合到一个矩阵中。
    • 4. 矩阵博弈分析中的矩阵元素表示参与者在不同策略下的收益，通过比较不同策略的收益来确定最优策略。
    • 5. 矩阵博弈分析可以应用于多种类型的博弈，如囚徒困境、寡头竞争等，帮助参与者制定最优策略。
    • 6. 矩阵博弈分析在经济学、政治学、军事学等领域都有广泛应用，为决策者提供有益的参考。
    • 7. 矩阵博弈分析可以用于研究多人参与的复杂博弈，通过分析各参与者的相互影响来寻找均衡解。
    • 8. 矩阵博弈分析中的均衡解通常采用纳什均衡或优势策略均衡等概念来描述，反映了各参与者的最优策略组合。
    • 9. 矩阵博弈分析在理论和实践上都具有重要价值，有助于提高决策者的分析和判断能力。
• 博弈论案例
  • 囚徒困境
    • 1. 囚徒困境是博弈论中的经典案例，描述了两个囚犯因合作或背叛而产生的不同结果。
    • 2. 在囚徒困境中，个体追求自身利益最大化可能导致集体利益受损。
    • 3. 囚徒困境揭示了人类决策中的社会困境，即合作与竞争并存。
    • 4. 通过囚徒困境，博弈论探讨了个体理性与集体理性的矛盾与平衡。
    • 5. 囚徒困境为政策制定者提供了思考如何在个体利益与集体利益之间找到平衡的思路。
  • 智猪博弈
    • 智猪博弈：
    • 1. 描述了两个个体在博弈中的策略选择和结果。
    • 2. 大猪选择行动，小猪选择等待。
    • 3. 大猪获得正收益，小猪获得负收益。
    • 4. 多次博弈后，小猪将选择行动以避免再次亏损。
    • 5. 纳什均衡为（行动，等待）。
  • 斗鸡博弈
    • 以下是关于“斗鸡博弈”的8个简短小点：
    • 1. 定义：斗鸡博弈描述两个强者在对抗时可能陷入的僵局。
    • 2. 场景：比如两个人互相瞪眼，谁先退让谁就可能被视为弱者。
    • 3. 策略：常见的策略包括“威慑”和“妥协”，但有时没有明确的赢家。
    • 4. 风险：如果不及时止损，双方都可能遭受重大损失。
    • 5. 理性选择：在斗鸡博弈中，理性往往意味着寻找双方都能接受的解决方案。
    • 6. 长期视角：避免陷入这种博弈，从长远角度看是更明智的选择。
    • 7. 外部因素：有时，外部因素如规则、法律或社会压力会影响斗鸡博弈的结果。
    • 8. 启示：斗鸡博弈提醒我们，在冲突中寻找共同利益和平衡是至关重要的。
    • 以上内容仅供参考，如需更多信息，建议查阅相关书籍或咨询专业人士。
  • 鹰鸽博弈
    • 1. 鹰鸽博弈：描述两种动物的行为选择对博弈结果的影响。
    • 2. 零和与非零和：区分鹰鸽博弈为零和与非零和博弈。
    • 3. 重复博弈：研究鹰鸽博弈在重复进行时的策略选择。
    • 4. 演化博弈：探讨鹰鸽博弈在演化过程中的策略演变。
    • 5. 混合策略：分析鹰鸽博弈中混合策略的运用及其影响。
    • 6. 实际应用：将鹰鸽博弈的原理应用于现实生活中的决策问题。
• 博弈论在现实生活中的应用
  • 经济领域
  • 政治领域
  • 军事领域
  • 商业领域
• 博弈论的未来发展
  • 博弈论与其他学科的交叉融合
  • 博弈论在复杂系统中的应用
  • 博弈论在AI和机器学习中的应用
    • 1. 博弈论为AI提供决策制定框架。
    • 2. 博弈论在机器学习中用于优化算法。
    • 3. 博弈论在推荐系统中应用，提升用户体验。
    • 4. 博弈论在金融风控中，降低风险。
    • 5. 博弈论在自动驾驶，提升交通效率。
    • 6. 博弈论在医疗健康，助力精准决策。
    • 7. 博弈论在环境保护，促进可持续发展。
    • 8. 博弈论在网络安全，增强系统防御。
    • 9. 博弈论在未来发展中，与多学科融合创新。
• 结论
  • 博弈论的重要性
    • 1. 博弈论揭示了决策的相互影响
    • 2. 博弈论有助于预测和解释行为
    • 3. 博弈论为政策制定提供理论支持
    • 4. 博弈论有助于解决现实世界中的问题
    • 5. 博弈论是研究合作与竞争的科学
  • 博弈论的应用前景
  • 博弈论对个人和组织的启示
    • 1. 博弈论揭示了决策过程的复杂性，对个人和组织而言，需要学会权衡利弊，选择最优策略。
    • 2. 博弈论有助于理解竞争与合作的关系，个人和组织应学会在竞争中寻求合作，实现共赢。
    • 3. 博弈论提醒我们考虑对手的反应，制定策略时要预见到对方的策略调整，保持灵活性。
    • 4. 博弈论强调信息的重要性，个人和组织应学会收集、分析信息，以制定更明智的决策。
    • 5. 博弈论的应用有助于个人和组织提高决策效率和准确性，实现更好的结果。