导图社区 CPA 财管 第3章 价值评估基础
- 25
- 1
- 举报
CPA 财管 第3章 价值评估基础
根据郑晓博老师讲义整理。 本章是原教材第三章和第六章的合并。 货币时间价值和风险是贯穿财务管理决策的两大基本观念,是资本成本、投资项目资本预算、证券价值评估、企业价值评估和长期筹资决策的基础。这两个知识点对理解财务管理的基本原理和决策方法意义重大,对后续多个章节的学习以及计算影响深远。 债券及股票的估值模型及其报酬率的计算是上述货币时间价值和风险的具体运用。债券到期收益率、普通股期望报酬率的计算与第四章资本成本计算的原理相同,计算资本成本是站在投资者的视角,如果不考虑筹资费用和所得税的影响,投资者要求的必要报酬率就是筹资者的资本成本。
编辑于2023-12-20 16:27:48- 价值评估基础
- 第3章
- 第三部分 职场进阶,成为一个领导者
《从总账到总监》:财务人员的进阶之路,太精彩了,这是第三部分笔记!《从总账到总监》是一本非常值得一读的书籍,它不仅让我看到了财务人员职业发展的过程还让我认识到什么才是真正的财务管理。书中大部分案例都始于财务,但并不终于财务,让我对职场和人生有了更深刻的认识。通读全书,其实并没有特别深奥难懂的财务专业知识,所有的知识点,都来源于日常工作与生活。在我看来,这本书对于那些对财务管理感兴趣的人来说是一本不可多得的读物。读完之后,我相信很多人都会跟我有同样的想法:如果现实中自己的上司像Bob那样该有多好啊!
- 《从总账到总监》第二部分 为成为优秀的财务人储备能量
《从总账到总监》:财务人员的进阶之路,太精彩了,这是第二部分笔记! 《从总账到总监》是一本非常值得一读的书籍,它不仅让我看到了财务人员职业发展的过程还让我认识到什么才是真正的财务管理。书中大部分案例都始于财务,但并不终于财务,让我对职场和人生有了更深刻的认识。通读全书,其实并没有特别深奥难懂的财务专业知识,所有的知识点,都来源于日常工作与生活。在我看来,这本书对于那些对财务管理感兴趣的人来说是一本不可多得的读物。读完之后,我相信很多人都会跟我有同样的想法:如果现实中自己的上司像Bob那样该有多好啊!
- CPA 财管 第十九章 业绩评价
根据郑晓博老师讲义整理。 本章主要介绍财务业绩评价与非财务业绩评价、关键绩效指标法(KPI)、经济增加值(EVA)以及平衡计分卡(BSC)的知识。 本章内容与第一章财务管理目标、第二章财务报表分析和财务预测、第四章资本成本、第十八章责任会计等章节有一定联系。
CPA 财管 第3章 价值评估基础
社区模板帮助中心,点此进入>>
- 第三部分 职场进阶,成为一个领导者
《从总账到总监》:财务人员的进阶之路,太精彩了,这是第三部分笔记!《从总账到总监》是一本非常值得一读的书籍,它不仅让我看到了财务人员职业发展的过程还让我认识到什么才是真正的财务管理。书中大部分案例都始于财务,但并不终于财务,让我对职场和人生有了更深刻的认识。通读全书,其实并没有特别深奥难懂的财务专业知识,所有的知识点,都来源于日常工作与生活。在我看来,这本书对于那些对财务管理感兴趣的人来说是一本不可多得的读物。读完之后,我相信很多人都会跟我有同样的想法:如果现实中自己的上司像Bob那样该有多好啊!
- 《从总账到总监》第二部分 为成为优秀的财务人储备能量
《从总账到总监》:财务人员的进阶之路,太精彩了,这是第二部分笔记! 《从总账到总监》是一本非常值得一读的书籍,它不仅让我看到了财务人员职业发展的过程还让我认识到什么才是真正的财务管理。书中大部分案例都始于财务,但并不终于财务,让我对职场和人生有了更深刻的认识。通读全书,其实并没有特别深奥难懂的财务专业知识,所有的知识点,都来源于日常工作与生活。在我看来,这本书对于那些对财务管理感兴趣的人来说是一本不可多得的读物。读完之后,我相信很多人都会跟我有同样的想法:如果现实中自己的上司像Bob那样该有多好啊!
- CPA 财管 第十九章 业绩评价
根据郑晓博老师讲义整理。 本章主要介绍财务业绩评价与非财务业绩评价、关键绩效指标法(KPI)、经济增加值(EVA)以及平衡计分卡(BSC)的知识。 本章内容与第一章财务管理目标、第二章财务报表分析和财务预测、第四章资本成本、第十八章责任会计等章节有一定联系。
- 相似推荐
- 大纲
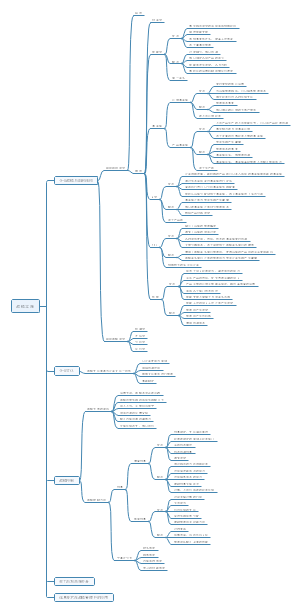
第三章 价值评估基础
本章概述
困心横虑,正是磨练英雄,玉汝于成。 ——曾国藩
知识结构
1. 利率基本知识
期限结构
收益曲线
组成部分
表达形式
2. 终值现值计算
复利终值和现值的计算
年金终值和现值的计算
3. 统计基础知识
平均趋势
离散程度
相互关系
投资组合
4. 投资组合理论
机会集
有效边界
资本市场线
证券市场线
5. 债权股票价值评估
债权价值和到期收益率
股票价值和到期收益率
第1部分 利率基本知识
【1】利率期限结构的含义
1. 利率期限结构的含义
利率期限结构(Term Structure)
[1]同一时点不同期限债券到期收益率与到期期限之间的关系
[2]也即: 长期利率和短期利率之间的关系
2. 即期利率与预期利率(理解不记)
即期利率6%
短期预期利率7%
只有一年,是短期
存一年,再存一年
本利和=100*1.06*1.07=113.42元
中间有选择权
两年期利率6.5%
中间没有选择权(流动性变差)
本利和=100*1.065*1.065=113.42元
【2】收益率曲线的含义
1. 收益率曲线的定义(理解不记)
收益率曲线(Yield Curve)是利率期限结构在图像上的表现
根据实际情况描绘出来的,不是推测。是实际现象,理论是为了解释这种现象。
2. 收益率曲线的形态
【3】利率期限结构理论概述
无偏预期理论=纯粹预期理论=预期理论
另外两项是有偏的理论
关系1
[无偏预期理论]和[市场分割理论]是两个极端,两者的假设和结论截然相反
[流动溢价理论]是折衷的理论
关系2
[无偏预期理论]认为利率完全由预期决定。利率是无偏的。
射击
[流动溢价理论]和[市场分割理论]是有偏预期理论认为除预期之外,其他因素也影响利率期限结构
利率期限结构理论
基本假设
主体
客体
市场
基本理论
长期和短期利率关系
现象解释
收益率曲线的不同形态
【4】无偏预期理论
1. 基本假设
主体:投资者对不同期限,没有偏好
佛系
客体:不同市场完全可以相互替代
长期可卖,短期续存
市场:资金长短期完全自由流通
哪边收益高,资金流向哪里
2. 基本理论
当前短期,即期利率是已知的
教材表述
利率期限结构完全取决于市场对未来利率的预期
长期即期利率是短期预期利率的函数或无偏估计
例题
2年期利率不是总共多少利息,是平均每年得到的利息。
按照预期理论,两种方案应当获得等量的资金。
3. 现象解释
预期理论认为,不同收益率曲线,是市场预期导致的。
上斜:长期比短期看起来高
另一个比自己高,才能拉高平均值
上升:未来利率比现在利率高
4. 主要缺陷
投资者对未来短期利率具有确定预期
资金在长期和短期资金市场之间的完全自由流动
【5】市场分割理论
1. 基本假设
主体:每类投资者较为固定地限制于某一期限的债券
上市公司资金,只能短期,流动性好的产品
客体:不同期限的债券根本无法相互替代
市场:市场按期限分割为相互隔离的细分市场
2. 基本结论
数量,横轴。价格,纵轴
教材表述
即期利率完全由各个期限市场上的供求关系决定
某一市场的变化不影响其他市场的供求或利率
思考: 假设央行开展 MLF 操作(medium-termlending facility中期借贷便利),在中期资金市场上注入的资金。
3. 解释收益率曲线
市场分割理论认为,不同收益率曲线,是市场供求导致的
VS预期理论认为,不同收益率曲线,是市场预期导致的
4. 缺陷
无法解释
不同期限的利率所体现的同步波动
长期利率随短期利率波动呈现规律性变化
【6】流动性溢价理论
1. 基本假设
主体:投资者偏好于短期债券,即存在流动性偏好。
客体:不同期限债券可以替代,但并非完全替代品。
市场:长期债券若要吸引资金,需要给出流动性溢价。
2. 理解流动性偏好和流动性溢价
流动性偏好
期限越长,利率风险越高。规避风险。
流动性溢价
对缺乏流动性的补偿
期限越长,越缺乏流动性
抬高了长期利率
VS风险溢价
风险越高,风险溢价越高
3. 基本理论
长期利率=短期内预期短期利率的平均值+流动性溢价
流动性溢价 =
LPR liquidity risk premium
短期利率能够影响长期利率,当不能唯一的决定长期利率。
4. 对收益率曲线解释
【7】利率期限结构理论总结
1. 三种理论各自假设
2. 各自理论
市场分割:把问题推给市场供求
3. 对收益率曲线的解释
4. 习题
A预期理论,B市场分割,C流动溢价
第2部分 终值和现值的计算
【8】货币时间价值和利率构成
1. 货币时间价值含义
货币时间价值(time value of money)
三个要素
货币
现金流
时间
时间轴
增值
增值率
2. 货币时间价值构成
A. 等待的补偿
实际无风险利率
B. 通胀的补偿
通货膨胀溢价
名义无风险利率
名义:包含通胀
无风险:不包含风险
C. 风险的补偿
违约风险溢价
流动性风险溢价
期限风险溢价
3. 市场利率构成
r = r*+IP+DRP+LRP+MRP
r*
纯粹利率,实际(真实)无风险利率
没有通胀,没有风险,的平均利率
短期政府债券的利率
短期无通胀
政府无风险
IP
Inflation Premium 通货膨胀溢价
为抵销通货膨胀对投资资金实际购买力的侵蚀,所要求的补偿
衡量:预计的平均通货膨胀率
rf=r*+IP
名义无风险利率(无风险利率)
是纯粹利率与通货膨胀溢价之和。rf(risk free)=r*+IP
衡量:政府债券利率
风险溢价
DRP违约风险溢价(Default Risk Premium) 违约风险=发行人不能按约定足额支付本利的风险
LRP流动性风险溢价(Liquidity Risk Premium) 流动性风险=不能短期内以合理价格变现的风险
MRP期限风险溢价(Maturity Risk Premium)
期限风险=债券因面临持续期内市场利率上升导致价格下跌的风险,也叫"市场利率风险"。(后续解释原理)
来源:市场利率上升
体现:价格下跌
期限越长,对利率的变动就越敏感
【9】单利计息和复利计息
单利计息
本利和=本金×(1+利率×期数)
复利计息
本利和=本金×(1+利率)^期数
【10】时间轴的说明
时间点和时间段组成
终值、现值计算的本质
【11】复利终值计算
1. 复利终值的概念
F
FV
本利和
2. 复利终值的计算
3. 复利终值系数
【12】复利现值计算
1. 复利现值的概念
P
PV
本金
2. 复利现值的计算
3. 复利现值系数
4. 复利终值和现值的比较
复利终值和复利现值互为逆运算
终值系数和现值系数互为倒数
【13】年金的概念与类型
1. 年金概念
概念
针对一次性款项 a lump sum payment
针对一系列款项 a series of payments
年金(Annuity),记做 A,是指间隔期相等的一系列等额款项。
2. 年金的四种形式
普通年金
预付年金
递延年金
永续年金
3. 子主题
【14】普通年金
从第一期开始,每期期末首付款的有限笔年金。
第一期,不递延
期末,不预付
有限,不永续
【15】普通年金终值计算
1. 逐笔折算
2. 加总求和
3. 公式简化
F=A×[(1+i)^n-1]/i
【16】普通年金现值计算
1. 逐笔折算
2. 加总求和
3. 公式简化
F=A×[1-(1+i)^-n]/i
终值和现值应试提示
考场上怎么写,怎么算?
【17】偿债基金和投资回收
1. 互为倒数关系
借入贷款,偿债。实际上是投资回收系数。
普通年金终值 VS 偿债资金
普通年金现值 VS 投资回收系数
2. 偿债基金系数
未来某一时点
到期偿债
3. 投资回收系数
回收初始投入资本
初始投资
4. 后续章节内容提示(等额年金和平均年成本)
【18】预付年金
1. 预付年金的含义
2. 预付年金终值和现值
3. 乘数调整法
F/A预付=F/A普通×(1+i)
P/A预付=P/A普通×(1+i)
4. 期数系数法
预付年金终值
期数加一,系数减一
预付年金现值
期数减一,系数加一
【19】递延年金
1. 概念
2. 终值
3. 现值
两步折现法
P=A×(P/A,i,n)×(P/F,i,m)
假想现金流法
P=A×[(P/A,i,m+n)×(P/A,i,m)]
先算终值法
P=A×[(F/A,i,n)×(P/F,i,m+n)]
4. 练习
第5年年初=第4年年末。第4年有收入,递延3年。
【20】永续年金
概念
现值
P=A÷i
【21】永续增长现金流的折现
1. 从永续年金到永续增长
更适用于股票价值评估
D代表股利dividend,r代表折现率,g代表增长率growth
默认D0不包含在现值中,现值第一笔现金是D1
2. 永续增长现金流的分布规律
3. 永续增长现金流的现值
V0=D0×(1+g)/(r-g)
V0=D1/(r-g)
4. 永续增长模型的适用前提
固定增长g
永续增长
D0到D1的增长率,即使不等于永续增长率g,也可以按永续增长模型计算
【22】带递延期现金流的折现
两步折现法的基本逻辑
递延期期数的确定
最早一笔钱,向前看一期
子主题
现值计算汇总练习
熟练和技巧
总结
2016
【23】多重折现率
折现率 VS 增长率
【24】利率表达形式的含义与换算
1. 各种表达形式的含义
报价利率
金融机构提供的利率
默认年利率
名义利率(含通货膨胀率)
要与复利次数n同时提供
计息期利率
每个计息周期,计付利息所依据的利率。(期间利率)
计息期利率=报价利率÷复利次数n
有效年利率
使以下:资金增值效果相等的年利率(等价年利率)
按计息期利率计息,每年复利n次。按有效年利率计算,每年复利1次。
有效年利率=(1+计息期利率)^n-1
2. 利率表达形式换算关系
【25】利率表达形式的应用
1. 票面利率,必须是报价利率
2. 资本成本和到期收益率,必须是有效年利率
3. 不同方案比较,应当在有效年利率口径进行
4. 终值、现值计算,应当在计息期口径计算
5. 题干给出“年折现率”或“折现率”,视为有效折现率
【26】复利次数变化的影响
1. 结论
复利次数为多次时
有效年利率>报价利率>计息期利率
给定报价利率
复利次数越多,计息期利率越低
复利次数越多,有效年利率越高
2. 有效年利率复利次数关系图像
给定报价利率,有效年利率随复利次数增加而增加,但不是线性递增,增速是逐渐放缓的。
有效年利率会达到极限值(渐近线)。
【27】连续复利的概念和计算
1. 连续复利的概念
计息期趋近于无限短
2. 连续复利的相关公式
有效年利率
有效年利率=
rc连续复利报价利率,c=continuous
连续复利终值
利率为rc,连续复利,t年后取出
连续复利现值
为了t年后能取得F,现在存款
复利终值和复利现值互为逆运算
系数互为倒数
连续复利利率
rc*t=ln(F/P)
rc=ln(F/P)/t
3. 相关计算说明
搜狗输入法:exp()
exp(0.08)-1=0.083287067675
exp(0.08/2)*500=520.405387096
600/exp(0.08*3)=471.97671664
ln(600/500)/3=0.0607738522647
第3部分 统计基本知识
概论
单一变量
期望值/均值
方差/标准差
变异系数
变量之间
协方差
相关系数
贝塔系数
【28】单一变量特征:告知概率
1. 给取值和概率:离散型分布
2. 期望值
Expectation
3. 方差
variance
var
s2
理解方差的定义式
理解方差计算式
方差=平方的期望-期望的平方
大-小
4. 标准差
Standard Deviation
st dev
s
更长用的总风险
5. 变异系数
标准差是绝对数,可比性差,收到规模(期望值)影响
3只羊
300只羊
变异系数 CV=标准差/期望值
= s/E(R)
3只羊,1/3
300只羊,1/300
变异系数经济含义
(1) 没有单位,相对数
(2) 变异系数衡量相对风险
(3) 期望值衡量期望报酬率,标准差衡量总风险。
(4) 变异系数衡量单位期望报酬率承担的总风险
6.
【29】单一变量特征:未知概率
1. 均值
每天体重,一个变量
x bar
2. 方差
总体方差 1/n
样本方差 1/(n-1)
3. 标准差
XX均值-均值XX
4. 变异系数
5.
6. 练习
历史长河中,只选择了5年,样本方差。
【30】变量之间关系:协方差
covariance,cov
1. 协方差的含义
协方差,前缀co+方差variance
cov
sxy
2. 协方差的计算
定义式
先求差,再求积,算平均
总体口径 ÷n
计算式
乘积的均值 - 均值的乘积
XX均值-均值XX
方差
平方的均值-均值的平方
XX均值-均值XX
3. 协方差的解读
协方差的取值
等于0,大于0,小于0
理解取值的正负
协方差为正,同向变动
协方差为负,反向变动
4. 协方差比方差更重要
(1) 随着组合中证券数量增多,协方差越来越重要,方差越来越不重要
(2) 当组合中证券数量较多时,组合风险(总方差)主要取决于协方差,方差是次要的。
(3) 当组合包含所有证券时(充分投资组合),组合风险(总方差)完全取决于协方差,方差是无关的。
【31】变量之间关系:相关系数
corr,r,coefficient of correlation,
1. 相关系数的计算和解读
相关系数(Coefficient of Correlation)corr,或r
一个协方差,除两个标准差
解读:相关系数没有单位,消除了两个变量变化幅度(方差)的影响,而只是单纯反应两个变量每单位变化时的相似程度
2. 相关系数的取值范围
[-1,+1]
3. 协方差和相关系数的关系
4. 协方差和相关系数相关公式
【32】回归分析初步
1. 历史数据
可靠的
历史数据
2. 模型假设
简单线性关系
3. 参数估计
(1) 最小二乘法的含义
如何让数据点与直线之间距离的平方之和最小?
用最小二乘法(OLS)来求解α和β
(2) 估算斜率和截距
(3) 估算斜率和截距(简易方法)
β=分子:协方差。分母:方差。
第4部分 投资组合理论
【01】投资组合的风险和报酬
1. 风险概念
风险是不确定性
负面效应
正面效应
财管中风险
与收益相关的风险
收益的不确定性
2. 单项资产风险和收益的衡量
假设一项资产的收益率是不确定的(随机变量)
收益率的期望值r代表该项资产的收益
收益率的标准差s代表该项资产的风险
先看坐标:纵坐标是概率。
横坐标收益。中轴线重合,期望值相等。
甲更靠拢期望值。
乙风险更高,D选项
3. 从单项资产到资产组合
【02】两项资产投资组合
1.
2. 理解两项资产组合方差公式
(1) 理解含相关系数的公式
组合方差=两个平方项+两倍交叉项
(A+B)^2=A^2+B^2+2r12AB
(2) 理解相关系数对组合方差标准差的影响
r12取值越高,方差越高
标注差越高
(3) 理解含协方差的公式
3. 理解相关系数对组合标准差计算的影响
(1) r12=1时
σ 组合=σ1w1+σ2w2
标准差的加权平均
只有r12=1时
组合的收益是各个收益的加权平均
均成立
(2) r12<1时
σ 组合 < σ1w1+σ2w2
(3) r12=-1时
σ 组合=|σ1w1-σ2w2|
绝对值
可能的最小值
4. 理解组合变异系数的计算方法
5. 两项资产组合习题汇编
组合标注差,随系数提高而增加,相关系数[-1,1]。
r12=-1时
组合标准差=5%
r12=1时
组合标准差=11%
【3】预备知识(1)
【4】预备知识:均值方差体系
1. 投资组合理论
2. 均值-方差分析框架假设
投资者追求单期财富的期望效用最大化。
收益和风险为基础进行组合选择。
收益用均值衡量,风险用方差(标准差)衡量。
3. 理解投资者的选择
4. 理解无效集有效集
5. 理解风险的高低
引入机会集
1.
2. 引入风险资产
都是风险,都是风险资产
3. 投资者选择
4. 引入机会集曲线
投资者选择体现为投资比例(高风险资产比重:低风险资产比重)
选择的结果体现为风险报酬的搭配(组合报酬率&组合标准差)
【5】机会集的定义
1. 机会集描绘随着对两种证券投资比例的改变,投资组合风险和报酬之间的权衡关系。
2. 机会集代表“可得”的投资组合;所有"可得"的投资机会只能出现在机会集上,不会在曲线上方或下方。
高低收益组合,可得。
3. 改变投资比例,只会改变组合在曲线上的位置。 改变相关系数,才改变曲线本身。
【6】机会集特征:向左弯曲
1. 机会集特征
向左弯曲现象
风险分散效应(有无与强弱)
最小方差组合
最安全投资方案
疆界四至
最高,最低风险报酬
2. 假设两项资产完全正相关(相关系数=1)
报酬率=各资产报酬率的加权平均
标准差=个资产标准差的加权平均
3. 假设两项资产非完全正相关(相关系数<1)
报酬率=各资产报酬率的加权平均
标准差<个资产标准差的加权平均
机会集(曲线)是向左弯曲的曲线。 此时有风险分散效应。
4. 相关系数各种典型取值
风险分散效应有无
相关系数
(1)相关系数会影响风险分散效应,相关系数越小,风险分散效应越强;
(2) 相关系数不影响组合的期望报酬率,不影响组合的系统风险。
5. 相关系数不影响组合的期望报酬率,不影响组合的系统风险。
【7】风险分散效应的强弱
1.
2. 相关系数对风险分散化效应影响
子主题
子主题
3. 分阶段考察风险分散效应强弱
子主题
4.
5. 左凸现象,有无效集
【8】机会集特征:最小方差组合
1. 引入最小方差组合
最小方差组合(Minimum Variance Portfolio 简称MVP)
与直觉相反,拿出部分资金投资于高风险资产比将全部资金投资于低风险资产的组合标准差还要小,更安全。但一定如此吗?
2. 分阶段考察最小方差组合位置
子主题
【9】机会集特征:四个界限
1. 最高收益、最低收益、最高风险
相关系数不影响组合的期望报酬率,不影响组合的系统风险。
相关系数能够降低风险,不能提高风险。
机会集(曲线)上界/下界/右界都是固定的,不受相关系数影响;
机会集(曲线)左界会受到相关系数的影响
2. 最低风险(分阶段考察)
不够小,固定。足够小,活动左界。
【10】有效边界
1. 有效边界的含义
机会集是“可得”的。
无效集:鄙视
有效集:“可得”且“想要”
有效边界
图像表现
经济含义
阶段特征
2. 有效边界的图像表现
3. 有效边界的经济含义
没有人愿意持有无效集中的投资组合
4. 分阶段考察有效边界
【11】相关系数变化的两个阶段总结
【12】多项资产的机会集和有效边界
1. 多项资产组合机会集
2. 多项资产组合有效边界
【13】引入无风险资产
1. 子主题
2. 引入无风险资产(F)
双向通行:贷出资金,借入资金。
双向固定:借入贷出利息相等。Rf
无风险资产标注差:sf=0
无风险资产的期望收益率:Rf>0
等待的补偿,通胀的补偿
3. 引入资本市场线(CML)和市场组合M
切线为资本市场线 CML
4. 子主题
【14】资本市场线
1. 资本市场线
一线一点
资本市场线
市场均衡点
两公式
斜截式方程
两点式方程
2. 资本市场线必背三句话
(1) CML是从无风险点出发做(原)有效边界的切线
(2) CML 是无风险资产出现之后新的有效边界(“裁弯取直”)
(3) CML 反映持有不同比例无风险资产(F)与市场组合(M)情况下,风险和报酬的权衡关系。(FM 收音机组合)
3. 资本市场线新的有效边界
CML 是无风险资产出现之后新的有效边界
可得的
投资者在F和M之间分配资金,组合的风险和报酬是加权平均
想要的
4. 资本市场线反映风险收益的权衡
投资者选择=投资于无风险资产F和市场组合M的比例
选择的结果=特定的风险和报酬的组合,一定落在 CML 上
CML 体现持有不同比例的无风险资产和市场组合情况下风险和期望报酬率的权衡关系
5. 对比
机会集曲线
高风险、低风险 不同比例分配资金的组合
资本市场线
无风险资产、市场组合,不同比例分别配资金的组合
【15】市场组合
市场组合(Market Portfolio,M 点),也叫市场均衡点
六句话
市场组合是资本市场线与[原]有效边界的切点
市场组合是唯一有效(即最有效、最佳)的风险资产组合
风险资产组合,唯一有风险
市场组合是所有风险资产构成的,以各自的市值为权重
所有风险资产以各自的总市值为权数的组合
市场组合是所有投资者共同决定的,不受个人偏好影响。
市场组合的风险主要取决于协方差,而非方差
市场组合中不含非系统风险,只含系统风险
例题
【16】资本市场线的斜截式方程
坐标
纵轴=期望报酬率Ri
横轴=标准差 σi
斜率
(Rm-Rf)/σm
VS变异系数
变异系数=σ/Ri
【17】资本市场线的两点式方程
1. 投资者的个人选择
如前所述,资本市场线意味
(1)投资者不选个股,追踪大盘,一律持有市场组合
市场组合,食盐NaCl
(2)投资者的选择是无风险资产F 和市场组合M 的再组合
投资者口味,重口多放盐
自有资金比例Q,无风险资金比例1-Q
自由资金100,借入40,投入市场
Q=140/100=1.4。1-Q=-0.4。
2. 选择带来的风险报酬
组合的风险,完全来自市场组合
3. 资本市场线两点式方程(参数方程)
参数是Q和1-Q
Ri=Q×Rm+(1-Q)×Rf
σi=Q×σm
4.
【18】投资者选择与风险偏好
1. 四种类型投资行为
2. 投资者风险偏好的影响
风险厌恶的程度越深,投资者越靠近 F 点
投资市场组合的比率越少,Q 降低,风险降低,收益降低
风险容忍的程度越高,投资者越远离 F 点
投资市场组合的比率越多,Q提高,风险提高,收益提高
3. 资本市场线划分为两段(左下vs 右上)
【19】资本市场线分离定理
三句话
1. 最佳风险资产组合与个人风险偏好相分离
2. 确定市场组合和做出个人选择相分离
3. 管理决策与股东偏好相分离
一、最佳风险资产组合与个人风险偏好相分离
共同决定 VS 再组合Q个人偏好
二、确定市场组合和做出个人选择相分离
三、管理决策与股东偏好相分离
管理层在决策时不必考虑每位股东对风险的态度
证券价格信息完全可确定投资者所要求的报酬率
该报酬率可指导管理层进行决策
【20】风险的分类
1.导致风险原因
2.风险能否分散
当组合囊括所有风险资产,并按市值为构成比例时,组合是市场组合(M 点);
此时,组合是充分分散的,不再含非系统风险,只含系统风险
非系统风险是可分散风险,可以通过投资分散化来消除。
3.风险有无补偿
系统有补偿
非系统,无补偿
没有通过投资分散
不补偿
方差/标准差,衡量总风险,不是非系统风险。
方差/标准差,衡量的是系统风险和非系统风险
总结
【21】贝塔系数
1. 贝塔系数的经济含义
贝塔系数,度量特定资产或资产组合相对于市场组合而言的“系统风险”
贝塔系数能度量,特定资产对组合整体(系统)风险的贡献。
2. 贝塔系数计算方法
(1) 定义式
(2) 关系式
(3) 回归直线法
子主题
(4) CAMP公式
子主题
3. 贝塔系数影响因素
例题
4. 贝塔系数取值范围
5. 比较贝塔系数和相关系数
β偏相关性
【22】必要报酬率和期望报酬率
1. 必要报酬率期望报酬率含义
系统风险→必要报酬率
主观要求
现金流→期望报酬率
客观
净现值为0
2. 必要报酬率和期望报酬率的关系
超额收益驱动买卖,价格和收益反向变动
在均衡(完美)市场上,期望报酬率等于必要报酬率
3. 必要报酬率和期望报酬率应试说明
大多数考题默认市场均衡,解题时
一般不需要纠结两个报酬率之间的差别。
但当考题涉及到下列内容时,不能直接假设市场均衡
(1) 题目问:证券价格被高估还是低估
(2) 题目问: 投资者应该买入还是卖出
(3) 题干中:同时出现期望报酬率和必要报酬率
【23】资本资产定价模型(CAPM)
1. 资本资产定价模型 Capital Asset Pricing Model
简记作CAMP [kæpem]
2. CAPM模型公式
Ri=Rf+βi(Rm-Rf)
某项资产βi(Rm-Rf) VS 市场溢价Rm-Rf
对比
市场平均收益 Rm
市场风险溢价 Rm-Rf
3. CAPM模型两种考法
4. CAPM模型假设
CAPM模型的稍重要假设
CAPM模型的一般假设
没有税金,没有交易成本
【24】证券市场线
1. 对比
证券市场线 Security Market Line 简称为SML
横坐标贝塔系数,系统风险
必要报酬率
资本市场线 Capital Market Line 简称为CML
横坐标标准差,总风险
期望报酬率
2. 从机会集 到 证券市场线
3. 证券市场线要素
斜率
投资者每承担一单位系统风险,获得的补偿
市场风险溢价
【25】证券市场线和资本市场线
1.
截距都是Rf
均衡时,期望报酬率=必要报酬率
斜率
SML:Rm-Rf
CML:(Rm-Rf)/σm
2. 证券市场线和资本市场线比较
腾笼又换鸟,形似神不似
斜率(Rm-Rf)/βm,βm=1
理论基础
资本资产定价模型
有效边际理论
适用范围
SML,更广:任何资产组合
CML:有效组合 FM组合
不允许有非系统风险
描述现象
任何资产组合
市场均衡
风险和无风险构成的组合
3. 理解资本市场线和证券市场线的适用范围
(1) 有效组合,是不“掺杂”非系统风险的组合
(2) 系统风险是有补偿的风险,应当分配风险溢价。
(3) 非系统风险是无补偿的风险,不应当分配风险溢价。
4. 总结:风险报酬的权衡关系
子主题
必背
机会集曲线
描述了持有不同比例(风险资产)投资组合的风险和报酬之间的权衡关系
高风险
低风险
资本市场线
描述了持有不同比例无风险资产和市场组合情况下风险和(期望)报酬率的权衡关系
无风险
市场组合
证券市场线
描述了市场均衡条件下任何资产或组合的风险和(必要)报酬率的权衡关系
任何
资产
总结
重点
CML
是无风险资产出现后的有效边界
用于有效组合(不含非系统风险)
SML
用于单项风险资产
用于非有效组合(含非系统风险)
用于有效组合(不含非系统风险)
【26】证券市场线的变动
1. 证券市场线的平移
[练习1]如果预计通货膨胀率将要上升,而市场风险溢价保持不变,某项投资的必要报酬率将如何变化?
答:某项投资的必要报酬率将要上升
2. 证券市场线的旋转
厌恶程度普遍提高,无风险报酬率保持不变
3. 证券市场线上点的滑动
[练习3]如果投资者对风险的厌恶程度不变,无风险报酬率不变,某项投资系统风险增加,其必要报酬率将如何变化?
答:某项投资的必要报酬率将要上升。
4. 总结
【27】投资组合的贝塔系数
1.
2. 投资组合的贝塔系数
β的加权平均
不受各项资产相关系数的影响
3. 投资组合的必要报酬率
先算组合的贝塔系数,再利用 CAPM 计算组合必要报酬
先算各项资产必要报酬率,再加权平均计算组合必要报酬率
4. 练习
β可以是负数
知识总结:投资组合衡量指标
加权平均指标
期望报酬率
必要报酬率
贝塔系数
非加权平均指标
未告知相关系数,不能计算
方差
标准差
变异系数
组合变异系数等于标准差/期望值, 分母不受相关系数影响, 分子受其影响,所以变异系数也受其影响
第5部分 债权股票价值评估
第1部分 债券部分
债权估值
一个基本模型
三种具体情形
平息债券
零息债券
永续债权
两个特殊问题
多次付息
非整数时点
【1】债券价值计算-基本模型
1. 债券现金流和价值的计算
债权的价值=利息的现值+本金的现值
2. 现金流按票面口径计算
利息面对面原则
3. 折现率取决于当前等风险投资市场利率
折现率取决于当前等风险投资的市场利率
当前,等风险,市场
垃圾债权=高收益债权
反映风险,反映收益
折现率的多种表述
必要报酬率
当时市场利率
现行市场报酬率
债务资本成本
到期收益率
期望报酬率
4. 把握到期时间的概念
n=剩余到期时间
≠整个存续期限
≠已经过去的期限
【2】债券价值计算-平息债券
1. 平息债券的含义
等额
等距
2. 平息债权的价值计算
【3】债券价值计算-零息债券
零息债券的投资收益完全体现为折价,
所以也叫纯贴现债券
【4】债券价值计算-利随本清债券
到期一次还本 VS 到期一次还本付息
含义
利随本清可以视为"多年一次付息”,是"一年多次付息”的相反情形。
计算
默认单利计息
价值计算
【5】债券价值计算-永续债券
Vpd=Ipd/Rpd
债券价值计算练习题
计算t年后的某个时点的价值。
t年后,只能收到n-t年的利息
2012
资本利得,本金差额。
【6】债券价值计算-多次付息情形
1. 按计息期口径计算债券价值
(1) 多次付息时,债券价值计算,必须在计息期口径折现
本金其实可以按期间口径也可以按照有效口径折现
但是利息只有按照期间口径折现才是现实可行的。
(2) 票面利率和年折现率,都需要先统一换算到期间口径
题目中"票面利率”,视为报价口径的计息利率
题目中"年折现率”,视为有效年利率口径的折现率
(3) 设每年付息次数为m
期间利率=票面利率÷m
期间折现率=(1+年折现率)^(1/m)-1
2. 如何按计息期口径计算?
3. 教材公式的说明
4. 练习
I×(P/A,r有效,n)
【7】非整数时点的债券价值
【8】到期收益率的含义和本质
1. 股市看价格,债市看收益
债券的投资收益率通常用到期收益率(Yield To Maturity,简写做YTM)来衡量
含义
起点是现在买入价
假定中途不卖出
终点是持有至到期
计算
本质是内含报酬率
表现为有效年利率
计算通产用插值法
2. 到期收益率的含义
现行价格购买债券,一直持有至到期日,能获得的报酬率。
新发行债券
买入价=发行价
已发行债券
买入价=流通价
反映当前行情,具有时效性。
3. 到期收益率的本质是内含报酬率
到期收益率是特定折现率,是现值等于购入价格
使债券投资的净现值等于0
4. 对比
到期收益率 VS 内含报酬率
到期收益率是内含报酬率的特殊版本
子主题
【9】到期收益率计算-使用插值法
原理不重要,提高速度才是王道。
投资收益率=投资收益/投资成本
从粗算收益率出发,向票面利率方向去整百分数
5.34%→8%,得出6%
折现值和折现率之间存在反向变动关系
现值过低,下调折现率
现值过高,上调折现率
一步写出最终公式
【10】到期收益率计算-不用插值法
1. 只剩最后一期的债券,不用插值
证券价格和收益反向变动,跌价将导致收益率提高。
2. 到期一次还本付息,不用差值
子主题
子主题
3. 平价债券,不用差值
子主题
子主题
4. 例题
【11】到期收益率计算-多次付息情形
到期收益率表现为有效年利率
计息期利率是十字路口
子主题
【12】到期收益率的影响因素
1. 到期收益率的影响因素
影响
票面约定→当前市场价格→到期收益率
不影响
市场利率
到期收益率是债券的期望报酬率,是从现金流中倒推的。
市场利率是债券的必要报酬率,是用来对现金流折现的。
在债券价格给定的情况下,市场利率不影响到期收益率
后续价格波动
当前市场价格代表了投资成本,影响到期收益率。
假设持有至到期,后续价格波动不会影响到期收益率。
违约风险
票面约定决定了合同现金流,现金流金额越多,现金流发生的时间越早,对投资者越有利,到期收益率越高。
计算到期收益率,假定合同现金流按时足额支付,无违约风险。
2. 到期收益率的常考影响因素
债券发行价格越低,对投资者越有利,到期收益率越高
债券付息频率越高,对投资者越有利,到期收益率越高
3. 到期收益率和票面利率的比较关系
原点法则:假设债券刚发行,满足平价发行,按年付息
到期收益率=票面利率
按年付息
(1) 折价发行
到期收益率 > 票面利率
(2) 平价发行
到期收益率 = 票面利率
(3) 溢价发行
到期收益率 < 票面利率
平价发行
(1) 多次付息
到期收益率 > 票面利率
(2) 按年付息
到期收益率 = 票面利率
(3) 利随本清
到期收益率 < 票面利率
4. 九宫格
【13】债券投资决策标准
根据价值判断
(1)按价值标准判断,是将市场价值和市场价格比较,不是和票面价值比较
题目没有特殊要求,一般用价值判断
根据收益判断
(2) 按收益标准判断,是将到期收益率和必要报酬率比较,不是和票面利率比较
子主题
债券价值影响因素概述
到期时间缩短
折价上升
向面值靠拢
越来越不折价
评价不变
溢价下降
向面值靠拢
越来越不溢价
回归面值
【14】债券价值影响因素-利率
1. 通过数学公式
2. 通过主观逻辑
【15】债券定价基本原则
基本原则
利差形成价差
判断的口径
因为是同一债券,计息频率给定,统一到任意口径都可行
如果题目只要求判断发行状态,统一到有效口径最快捷
如果题目还要求计算债券价值,统一到期间口径最快捷
【16】付息周期对债券价值的影响
子主题
【17】债券价值影响因素-到期时间
1. 理解到期时间的变化
到期时间,当前日至到期日之间剩余的时间间隔。
表述
到期时间缩短
随着时间流逝
随着到期日临近
到期时间延长
债券期限延长
债券到期日推迟
2. 到期时间缩短对债券价值的影响
时间流逝→到期时间变短→折价溢价减少
→债券回归面值
3. 债券估值剪刀差原理
利差×期限≈价差
4. 总结
【18】债券运动轨迹-连续付息
1. 债券价值的变动趋势
2. 债券价值的运动轨迹
3. 债券运动轨迹平滑的条件
折现率不变
连续付息
【19】债券运动轨迹-间隔付息
1. 间隔计息的债券运动轨迹
债券周期性波动的根源,在于应计利息的扰动。
对比
应计利息是应付债券之中的明细科目(母猪肚里的小猪)
应收利息是应付债券之外的独立科目(已经出生的小猪)
2. 周期性特征
3. 趋势性特征
子主题
4. 高低点
(1)割息后,债券价值达到低点;低点价值不受应计利息的扰动,如实体现债券折价平价溢价的"本色”。
(2)割息前,债券价值达到高点;高点价值被应计利息所提升
子主题
【20】债券对折现率的敏感度
1. 随着到期时间缩短,债券价值对折现率的敏感程度逐渐降低, 即,折现率变动对债券价值的影响越来越小。
2. 案例计算
3. 图像把握
4. 引入久期(超纲)
5. 例题
答案ABCD,甲债券期限风险更高
债券价值影响因素总结与习题
债券价值
债券的价值是根据合同现金流和市场利率推算出来的。
现金流
市场利率
票面约定的合同现金流对投资者越有利,债券价值越高。
市场利率越低,债券价值越高。
市场价格不影响债券的价值。(轻一本章选择题涉及)
到期收益率
到期收益率是根据合同现金流和市场价格推算出来的
现金流
市场价格
票面约定的合同现金流对投资者越有利,债券收益越高
市场价格越低,债券收益越高。
市场利率不影响到期收益率。(轻一本章选择题涉及)
市场均衡
当市场均衡(题目中也可能表述为"市场有效”时,
债券(内在)价值=市场价格
债券到期收益率=市场利率(必要报酬率)
投资决策
如果考题问债券投资决策,意味着没有假设市场均衡
可以比较债券的价值和市场价格做出决策
可以比较到期收益率和市场利率做出决策
习题
债券价格不应现债券价值
必要报酬率低于票面利率 =>
溢价发行
A:市场有效 => 价格=价值
D:期限延长 => 平价价差不变
第2部分 股票部分
【21】股票价值评估-基本模型
1. 股票现在的价值是未来无限期股利的现值。 计算要对无限期股利逐笔测算、逐笔折现。
2. 通常假定 D0是已经发放的股利,不包含在股票价值 V0里面。股票价值中包含的最早的现金流是D1。
除非:个别题目表明D0需要计入股票价值中。
3. 不管投资者打算永远持有,还是未来卖出,基本公式都适用。 基本模型与持股意图无关
【22】股票价值评估-固定股利
永续年金
V0=D/Rs
【23】股票价值评估-固定增长
1. 固定增长模型的计算公式
计算公式
适用条件
注意事项
模型结论
V0=D1/(Rs-g)
2. 固定增长模型的适用条件
Rs大于g
固定增长
D0→D1,随意
永续增长
例题
3. 注意事项:判断股利性质
4. “三率相等”的结论
假设市场有效,在固定增长模型下,有三率相等
g
=股利增长率(模型假设)
=股价增长率(用于计算未来股价)
=资本利得率(用于计算期望报酬率)
市场有效,P=V
Pt=P0×(1+g)^t
例题
同时出现价格和价值,市场并非有效
默认市场均衡,价格=价值
【24】两阶段模型-理论划分
1. 进入稳定增长期的标志
投资回报率趋近资本成本率,意味着超额收益消失
功名富贵若长在,汉水亦应西北流---李白
销售增长率趋近经济增长率,意味着超速增长结束
飘风不终朝,骤雨不终日---老子
2. 经济增长率的含义
经济增长率=宏观经济的名义增长率
3. 稳定增长状态的表现
回忆第二章:可持续增长状态:在稳定状态下,经营效率和财务政策不变,财务报表将按照稳定的增长率在扩大的规模上复制。
本章尤其关注下列三个指标:
销售增长率(火车头)= 实体现金流增长率 = 股权现金流增长率
4. 两阶段划分:从理论到计算
高速增长期
详细预测期
稳定增长期
永续期
后续期
5. 例题
现金流折现,增量现金流和时间价值
稳定状态:报酬率,增长率
子主题
【25】两阶段模型-解题划分
教材说明:过渡期(第3年)股利的两处理方式
既可视为详细预测期终点,也可视为后续期起点
既可计入详细预测期[安全],也可计入后续期[快捷]
【26】两阶段模型-折现方法
注意
因为预测期有限,即使增长率固定,也不能用永续增长模型。
【27】两阶段模型-例题选讲
划分两阶段
测算现金流
折现计算
【28】股票期望报酬率-固定股利/固定增长
1. 股票期望报酬率计算逻辑
2. 固定股利模型下期望报酬率
Rs=D/P0
期望报酬率=股利/股价
3. 固定增长模型下期望报酬率
P0=D1/(Rs-g)=>
Rs=D1/P0+g
期望报酬率=股利/股价
Rs
股利收益率
=股利收益率+资本利得率
D1/P0
股利收益率
g
资本利得率
股价增长率=股利增长率=资本利得率
4. 多次支付股利的问题
股票期望报酬率必须用有效年利率形式表达
多次支付股利,需要先计算每个支付周期的报酬率,再转换为有效年利率
5. 例题
【29】股票期望报酬率-两阶段模型
假装是固定增长模型
附录
1. 2003 年考题(表格填空)解析
2. 基准利率和利率影响因素
基准利率
市场化:由供求关系决定
反映供求关系
反映未来预期
政策化:政府调控
货币政策目标的手段
子主题
基础性:
较强关联性
传递性:
传递市场信号和调控信号
影响因素
经济因素
政策因素
货币
政策
3. 预期理论对收益率曲线的解释
4. 样本方差的计算说明
取值是 n与平均值的差,自由度少一个
有了n-1个
有了平均值,可推出n的值
四个数,总和=0
第四个差额不能随意赋值
子主题
5. 协方差矩阵和相关系数矩阵
6. 三项资产和多项资产投资组合
7. 贝塔系数的回归直线法
8. 投资组合的贝塔系数
9. 普通年金终值系数推导
10. 永续年金现值系数推导
11. 永续增长模型的推导
12. 连续复利下的有效年利率
13. Rm和Rm-Rf 的表达
14. 资本市场线的相关证明
15. 债券的基本知识
16. 付息频率的影响(旧教材)
17. 债券定价原理的推导
18. 股票估值基本模型的适用范围
19. 股利增长率与股价增长率
20. Excel 与本章计算公式
营业现金毛流量
2-经营营运资本增加
3-资本支出
4-债务现金流
5-税后利息费用(付息部分)
6-净负债减少(还本部分
7-股权现金流
8-现金股利(对应付息部分)
9-股份回购(对应还本部分)