医学统计学与SPSS软件基础

"想用数据说话却不知从何下手？这份医学统计指南就是你的SPSS实战手册！" 内容涵盖：从基本概念、数据管理到SPSS操作全流程重点解析t检验、方差分析、卡方检验等假设检验方法详解直线回归与相关、Spearman等级相关的应用与区别附带四格表资料、随机区组设计等经典案例解析用最简明的语言带你掌握医学统计核心技能，零基础也能快速上手数据分析。

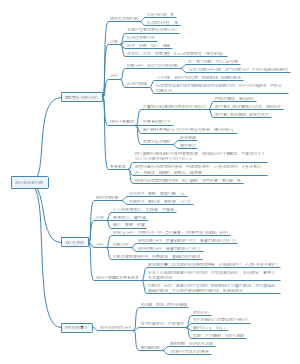
医学统计学与SPSS软件基础

• 学习目的
  • 掌握医学统计学基本概念和方法
  • 熟练应用SPSS软件完成基本统计分析
  • 文献辨析（选学）
• 基本概念与SPSS数据管理
  • 基本概念
    • 统计学（statistics)
      • 运用概率论和数理统计研究数据的收集、整理和分析
      • 医学统计学
        • 统计学应用于医学领域
      • 统计分析
        • 统计描述
        • 统计推断
          • 用已知的样本来推断未知的总体
        • 总体估计
        • 假设检验（重难点）
    • 总体(population)
      • 根据研究目的确定的同质观察单位的全体——通常数目庞大
        • 同质——相同性质、共同特征
      • 例：调查某地 1992年 健康 成年男性的身高。（有限总体——有时间和空间的限制）
      • 例：某种药物 治疗 高血压患者 的疗效。（无限总体——没有时间和空间的限制）
    • 样本(sample）
      • 从总体中随机抽取部分观察单位，其实测值的集合
        • 随机抽样……减少偏性，使样本对总体有代表性
        • 随机抽样的目的：用样本信息来推断总体特征（统计推断）
          • 用已知的样本来推断未知的总体——前提：随机抽样
    • 概率（probabiity）
      • 描述随机事件发生的可能性大小，用P表示
        • 例：某种新药治疗某种疾病的患者300人，治愈了240人，则治愈率为80%（频率）
          • 概率是未知的，在样本量足够大时，频率≈概率
      • 必然事件→P=1
      • 不可能事件→P=0
      • 随机事件→0<P<1
      • 小概率事件
        • 当一个事件的概率P≤0.05或P≤0.01时，称为小概率事件
          • P=0.05代表100次实验中有5次时间发生
        • 特点：某件事发生的可能性很小，在一次试验中基本上是不会发生的
    • 资料的类型
      • 数值变量（NumericalVariable）
        • 又称为定量资料或计量资料，其变量值是定量的，表现为数值大小，一般有度量衡单位
          • 例：血压，身高，体重，血脂等。
      • 分类变量 （Categorical Variable)
        • 又称为定性资料，其变量值是定性的，表现为互不相容的类别或属性
          • 无序分类变量（Nominal Variable)
            • 又称为名义变量。包括变量值取无等级顺序的二项分类或多项分类
            • 例：性别、血型等分类指标。
          • 有序分类变量（Ordinal Variable)
            • 又称为等级资料，各类之间有程度的差别，即变量值取有等级顺序的几类
            • 例：临床疗效可以分为痊愈、显效、好转、无效。
      • 不同类型的资料，统计方法不同。
        • 数值变量→t检验、方差分析、回归与相关（符合正态分布的数据）
        • 无序分类变量→卡方检验
        • 有序分类变量→秩和检验
      • 各种类型的资料之间可以相互转化。
        • 例：
    • 误差
      • 抽样误差——不能避免
      • 随机测量误差——不能避免
      • 系统误差——可以避免
      • 过失误差——可以避免
    • 统计工作的基本步骤
      • 统计设计
      • 搜集资料
      • 整理资料
      • 分析资料
  • SPSS数据管理
    • 变量标签、变量值标签
    • 排序、拆分
      • 语法执行模式
        • 拆分文件+描述
        • 取消拆分+描述
    • 选择个案
      • • • • • 运行统计描述语法即可得到相应的统计描述结果
        • 取消选择个案
          • • • 运行统计描述语法即可得到相应的统计描述结果
    • 计算变量
      • • • 返回数据库查看新变量
    • 重新编码
      • 能够将数值变量转化为分类变量——统计方法发生对应变化！！
      • • • 在数据窗口即可查看重新编码的变量
• 数值变量与分类变量
  • 统计描述指标
    • 数值变量
      • 数值变量的分布类型
        • 对称分布
          • 集中位置居中，左右两侧频数基本对称。
          • 常见正态分布
            • 正态分布曲线特征
              • 正态分布有两个参数：均数μ和标准差σ。常用N(μ,σ²)。
                • 均数μ又称为位置参数，决定了曲线的位置：μ越大，曲线越右移。
                • σ²为变异度参数：σ²越大，曲线越矮胖
            • 正态分布曲线下面积分布规律
              • (μ - σ, μ + σ)→68.27% (μ - 1.96σ, μ + 1.96σ)→95% (μ - 2.58σ, μ + 2.58σ)→99%
            • 标准正态分布
              • 任何正态分布经过标准化变换，都能转化成唯一的标准正态分布
              • 标准正态分布曲线下面积分布规律
        • 偏态分布
          • 集中位置偏向一侧，频数分布不对称。
      • 数值变量的统计描述指标
        • 集中趋势指标的描述
          • 1.算数均数（均数 mean）
            • 适用于正态分布
            • 总体均数：μ；样本均数：x
          • 2.中位数（median,M）
            • 主要适用于偏态分布资料
              • 对于偏态分布资料，中位数只和位置居中的观察值有关，适合描述偏态分布的集中趋势。
            • 中位数是指将一组观察值从小到大排列，位置居中的观察值
            • 例：
            • 对于近似正态分布，中位数和均数是近似相等的。
        • 离散趋势指标的描述
          • 1.极差或全距（range,R）
            • R=最大值-最小值
            • 计算简单，但是不能反映所有变量值的变异程度。
          • 2.方差（Variance,VAR）
            • 表示一组变量值的平均离散程度
            • 方差越大，离散程度越大。
            • • 总体方差通常是未知的
              • 样本方差实际上是用样本均数代替了总体均数
          • 3.标准差（Standard Devication,SD）
            • 也表示一组变量值的平均离散程度
            • 适用于正态分布
            • 医学论文中，标准差比方差更常用
              • 因为标准差的单位和均数的单位是一致的，更方便使用
          • 4.四分位数间距（Quartile,Q）
            • 主要适用于偏态分布资料
            • • P₇₅表示75%的数比它小，25%的数比它大。P₇₅又称上四分位数。
              • P₂₅表示25%的数比它小，75%的数比它大。P₂₅又称下四分位数。
            • 代表中间50%的数据的离散程度或变异程度
              • 不受两端极端数据的影响，较稳定，主要适用于偏态分布资料
            • 可以直接用四分位数表达偏态分布资料的离散趋势，形式如下：（P₂₅，P₇₅）。
        • 补充
          • 几何均数（geometric mean，G）
            • 常适用于一种特殊的偏态分布租赁：对正态分布资料
              • 常见于抗体滴度
          • 变异系数（coefficient of variation,CV）
            • 用于描述数据的相对离散程度
            • • 没有单位
              • CV可以>100%，也可以<100%
            • 在比较多组数据的离散程度时
              • 如果数据的度量衡不一样，此时不能应用标准差，而应该用变异系数
              • 当数据的均数相差悬殊时，也不能用标准差，而应该用变异系数
    • 分类变量的统计描述指标——相对数（Relative Number）
      • 比（Ratio）
        • 又称相对比。表示两个有关联的指标之比。
        • 例：性别比、BMI、OR、RR……
      • 比例（Proportion）
        • 事物内部各部分所占的比重（又称为构成比）。
        • 要求
          • 分母必须包含分子；
          • 分子、分母是性质相同的指标；
          • 各部分的比例之和为100%。
        • 例：
        • 患病率（Prevalence）
          • 表示在某时点上接受检查的人群中现患病例所占的比例
          • 此指标是比例（Proportion），不是率（Rate）
          • 病死率、有效率、治愈率、患病率……实质上都是比例，并不是真正意义上的率。
      • 率（Rate）
        • 表示单位时间内某事件发生的频率
        • 分子为观察期间内某事件的发生例数
        • 分母为观察人-时（Person-Time)总数，即∑（每个观察单位×观察时间）
        • 发病密度（Incidence Density,ID)
          • 观察期间内某疾病心法病例数/该观察期间内人-时总数
          • 实际应用中也可称为发病率（Incidence Rate）
          • 例：某研究调查45～49岁使用口服避孕药的妇女中乳腺癌的发病情况。此研究中，乳腺癌的新发病例数为9，观察人一年数为2935。则此调查人群中乳腺癌的发病密度为：9/2935=0.00307=307/10万人一年。
      • 注意事项
        • 计算率和比例的分母不宜过小；
          • 分母过小，则得到的相对数不稳定
        • 不能以比例代替率；
        • 多个率不能直接相加求平均。
          • 如需求平均律，应该用总的发生数除以总的观察例数。
  • SPSS软件的应用
    • 数值变量的统计
      • 作直方图或正态曲线帮助判断数据是正态分布还是偏态分布
        • • 运行语法
            • 在输出窗口查看直方图
          • 如需对另一个变量做直方图，如“alt”。语法快捷方式——复制粘贴本段语法，将"height"修改为“alt”，然后运行修改后的语法
            • 在输出窗口查看另一个变量的直方图
      • 数值变量的统计描述
        • • • 输出窗口查看统计描述 注意！ 根据不同指标的不同分布类型， 选择不同的统计描述指标！
    • 分类变量的统计描述
      • • 运行语法
          • 输出窗口查看统计描述
• 两组数值变量比较的假设检验
  • 一、 均数的抽样误差
    • 1. 定义
      • 在抽样研究者，由于抽样造成的样本均数与总体均数之间的差异或样本均数之间的差异，称为均数的抽样误差（Sampling Error，SE）
      • 抽样误差是不可避免的
        • 造成抽样误差的根本原因是个体变异的客观存在
    • 2. 例：调查某地1992年健康成年男性的身高
    • 3. 计算
      • 抽样误差的大小，即标准误
      • 标准误也可以称为样本均数的标准差
    • 4. 性质
      • 标准误与标准差成正比，与样本含量的平方根成反比
      • 试剂工作中减少抽样误差的有效方法是增大样本含量
  • 二、 t分布
    • 1. 定义
      • 若从正态分布N(μ,σ²)总体中随机抽取样本含量为n的样本，样本均数也服从正态分布N(μ,σ²)。
        • 服从标准正态分布N(0,1)。
        • 服从自由度ν=n-1的t分布
    • 2. 性质
      • 一组与自由度ν有关的曲线，随着ν增大接近标准正态分布。
        • 自由度决定形态：自由度ν = n - 1（n是样本量 ），不同自由度对应不同t分布曲线。比如ν = 1 时，曲线矮胖，离散程度大；ν = 5 时，曲线更集中，形态随ν变化
        • 趋近标准正态分布：当ν逐渐增大，t分布曲线越来越接近标准正态分布（ν→∞ )时，二者几乎重合 ）。像小样本（ν小）时，t分布更 “保守”，尾部概率比标准正态分布大；大样本下，就可近似用标准正态分布替代t分布做统计推断，体现了样本量对分布形态的影响 。
      • t分布与标准正态分布的区别
        • 标准正态分布是均数为0、标准差为1的一条曲线；而t分布是一组与自由度有关的曲线，并且随着自由度增大，t分布会趋近于标准正态分布。
      • t分布中界值与尾侧面积的关系
        • 当t分布曲线中间包含95%的面积时，两侧的界值称为0.05的t界值，此时外侧尾侧面积之和为0.05
        • 若某个t值的绝对值>0.05的t界值，其对应的尾侧面积之和<0.05
        • 若t值绝对值<0.05的t界值，对应的尾侧面积之和则>0.05
  • 三、 总体均数95%置信区间的估计
    • 1. 定义
      • 根据样本均数，计算出有(1 -α)的把握包含总体均数的数值范围，此范围即总体均数的置信区间 。(1 -α)为置信度，常取α = 0.05，对应 95% 置信度，用于估计总体均数 95% 置信区间。
    • 2. 计算
      • 背景实例
        • 随机抽取某市区 40 例居民膳食调查，人均摄入蛋白质样本均数Xˉ = 62.5g，样本标准差S = 5.6g，估计该市区人均摄入蛋白质总体均数的 95% 置信区间。
      • 计算步骤
  • 四、 假设检验的基本原理
    • 1. 核心概念
      • 检验假设
        • 考虑差异来源的两种可能性：
          • H0（无效假设）：假定样本与总体（或两组样本所代表总体 ）无本质差异，差异由抽样误差导致，如“难产男婴体重均数μ =正常男婴体重均数μ0” 。
          • H1（备择假设）：与H0对立，认为样本与总体（或两组样本 ）存在本质差异，如“难产男婴体重均数≠正常男婴体重均数μ0” ，反映研究者想得到的结论方向（双侧/单侧 ）。
      • 检验水准（α ）
        • 即显著性水准，是判断“是否拒绝H0的界限”，常取(α = 0.05) ，代表“小概率事件”的概率阈值 。
          • P≤0.05→拒绝H0→认为有差别
          • P＞0.05→不拒绝H0→认为无差别
    • 2. 基本逻辑 （小概率原理）
      • 前提：先假设H0成立 （如认为难产男婴与正常男婴体重均数相同 ）。
      • 推理：在H0成立前提下，计算样本统计量（如(t)值 ），判断其对应的概率(P) ：
        • 若P≤ 0.05：说明在H0假设下，出现当前样本情况是小概率事件。依据小概率原理，小概率事件在一次抽样中几乎不发生，故拒绝H0，接受H1 ，认为样本与总体（或两组 ）存在本质差异（如难产男婴体重均数和正常男婴不同 ）。
        • 若P > 0.05 ：说明在H0假设下，当前样本情况属大概率事件，无充分证据拒绝H0，故不拒绝H0 （注意不是“接受(H_0)”，只是暂未找到拒绝证据 ）。
    • 3. 实例关联 （难产男婴体重问题 ）
      • 已知正常男婴出生体重均数μ0= 3.26kg，抽取20名难产男婴样本。通过假设检验判断：若拒绝H0（μ =μ0 ），则认为难产男婴体重均数和正常男婴有差异；若不拒绝H0，则暂认为二者无本质差异（差异由抽样误差引起 ） 。
    • 4. 假设检验的思想贯穿于经典统计
      • 同样适用于方差分析、卡方、相关于回归所设计的假设检验
  • 五、 三种t检验
    • 1. 单样本t检验
      • 实例
        • 已知某地正常男婴出生体重均数(\mu_0 = 3.26kg)，随机抽取20名难产男婴，体重数据：3.5、3.5、3.2、3.5、3.3、3.0、3.3、3.2、3.4、2.7、3.4、3.6、3.5、2.8、3.4、2.9、3.5、3.5、4.0、4.0 ，推断难产男婴体重均数与正常男婴是否不同。
      • 基本原理
        • 用于一个样本均数与已知总体均数μ0的比较。
          • 又称样本均数与已知总体均数比较的t检验
        • 检验目的是推断未知总体均数μ是否等于μ0 。
          • 其检验假设为：
        • 计算公式：
          • 分子为样本均数减去已知总体均数μ0，分母为样本均数的标准误，自由度=n-1
      • 适用条件
        • 正态性
          • 样本对应总体服从正态分布。
          • 当数据偏离正态不是很严重时，t检验仍适用 。
    • 2. 两个独立样本t检验
      • 实例
        • 某医师测得12名正常人、13名病毒性肝炎患者血清转铁蛋白含量（g/L），判断患者与正常人含量有无差异。 正常人数据：2.61、2.71、2.73、2.64、2.68、2.81、2.76、2.55、2.91、2.85、2.71、2.64 患者数据：2.34、2.47、2.22、2.31、2.36、2.38、2.15、2.57、2.19、2.25、2.28、2.31、2.42
          • 正常人和病毒性肝炎患者的血清转铁蛋白含量测量都是独立的，所以是两个独立样本
      • 基本原理
        • 两个独立样本均数对应的总体均数为μ1、μ2，μ1、μ2是未知的。）
        • 检验目的是推断μ1与μ2是否相等。
          • 其检验假设为：
        • 计算公式：
          • 分子为两个样本均数之差， 分母为样本均数差值的标准误。
            • 标准误计算公式了解即可。
      • 适用条件
        • 正态性
          • 两个样本对应的总体分别服从正态分布。
          • 当数据偏离正态不是很严重时，t检验仍适用 。
        • 独立性
          • 两个样本的相互独立的，无关任何关联性
        • 方差齐性
          • 两个样本对应的总体方差相等
          • 用Levene方法检验是否满足方差齐性假定
          • 若违背了方差齐性假定，则常用如下统计方法
            • 校正t检验
            • 先变量变换，满足方差齐性后再行t检验
            • 两个独立样本的秩和检验
    • 3. 配对设计t检验
      • 基本原理
        • 常用于三种情况：
          • 1. 按照某些特征（性别、年龄等）先将两个受试对象配成对子，再对同一对子内两个个体分别给予处理
            • 例：
              • 每一个对子中的两个个体是相似的，按照性别和血清胆固醇水平进行了匹配 这两个样本是相关的，是不独立的！——配对设计与独立样本设计的本质区别。
          • 2. 把同一受试对象分成两部分，再分别给予两种不同处理
          • 3. 对同一受试对象处理前后的比较（自身对照设计）
            • 例：
        • 在配对设计中，设每一对子的两个观测变量为X、Y，差值d=X-Y ，d的样本均数对的应总体均数μ0是未知的。
        • 检验目的是推断μ0是否等于0，用于判断配对处理的效应差异 。
          • 其检验假设为：
        • 计算公式：
          • 分子为差值的样本均数，分母是差值的标准误。自由度=n-1，在这里n是对子数。
      • 适用条件
        • 正态性
          • 差值d对应的总体服从正态分布。
          • 当数据偏离正态不是很严重时，t检验仍适用 。
      • 配对设计t检验的统计效率高于两个独立样本t检验。
        • 把相似的个体配成对子，减少了误差
  • 六、 假设检验的注意事项
    • 1. 假设检验的目的
      • 推断两个总体均数是否相等。
    • 2. 假设检验方法的选择
      • 根据不同的研究设计类型，选择不同的方法。
    • 3. Z检验的应用
      • 实际工作中Z检验用于“总体标准差α未知，但样本量n较大” 的情况
      • Z 检验是 t 检验的近似方法 ，用于统计推断等场景
        • 实际工作中应用较少，一般直接用t检验
    • 4. t检验与置信区间的等价性
      • 单样本的t检验
        • 若接受H0，则样本值与已知总体均数差值的总体均数95%置信区间必包括0.
      • 两个独立样本的t检验
        • 若接受H0，则两独立样本差值的总体均数95%置信区间必包括0.
      • 配对设计的t检验
        • 若接受H0，则配对差值的总体均数95%置信区间必包括0.
    • 5. P值不能反映总体均数差别的大小
      • P值越小，越有把握认为两总体均数不相等。
    • 6. 假设检验的结论具有概率性
      • H0原本正确，但P≤0.05，拒绝H0：第一类错误α
        • 即拒绝了原本正确的
      • H0原本不正确，但P>0.05，不拒绝H0：第二类错误β
        • 即接受了原本错误的
      • α为事先指定的检验水准，β未知
      • α越小，β越大；α越大，β越小
        • 如果要同时减少这两类错误，需要增大样本量
    • 7. 功效（power）
      • 又称检验效能或把握度，是指当两总体确实有差别时，按检验水准α，能够发现两总体间差别的能力，即1-β。
        • 一般我们希望功效至少为0.8，对应的β=0.2
      • 要保证比较高的功效，很重要的条件是具有足够的样本量
        • 只有足够大的样本量，才能够减少二类错误β，保证比较高的功效1-β
    • 8. 专业意义与统计学意义是不同的
      • 差别有统计学意义，并不意味着一定有专业意义。
        • 即使差别非常小，没有专业意义，但有足够大的样本量，我们依然可以得到P<0.05，有差别的结论。
      • 反之，即便差别无统计学意义，但也可能具有专业意义。
        • 当样本量较小时，是有可能出现这种情况的。
    • 9. 参数统计与非参数统计
      • 参数检验
        • 概念：对样本所属的已知分布总体的未知参数进行估计或假设检验的这类统计推断方法。
        • t检验、卡方检验、相关与回归都属于参数统计方法。
      • 非参数检验
        • 概念：并非比较总体参数，而是直接比较分布，是一种不拘泥于总体分布的统计方法，它是通过将样本实际数据排序编秩次后，对秩次进行比较。
        • 若不满足参数检验条件，则适宜用非参数检验。
        • 会损失数据的信息。
          • 如果数据满足参数检验的条件，而采用非参数检验，那么有可能会降低统计检验效能。
        • 最常用秩和检验。
          • 两个独立样本的秩和检验（Wilconxon两样本比较法）
            • 设计类型与独立样本的t检验一样，但其数据服从偏态分布
            • 例：
          • 配对设计差值的符号秩和检验（Wilcoxon配对法）
            • 设计类型与配对设计的t检验一样，但其数据服从偏态分布
            • 例：
  • 七、 SPSS的应用
    • 单样本t检验
      • • 打开语法窗口运行语法
          • 输出窗口查看统计描述结果
    • 独立样本t检验
      • • 打开语法窗口运行语法
          • 输出窗口查看统计描述结果
    • 配对t检验
      • • 语法窗口运行语法
          • 输出窗口查看统计描述结果
    • 秩和检验
      • • 运行语法
          • 查看统计结果
    • 配对秩和检验
      • • 运行语法
          • 查看统计结果
• 多组数值变量比较的假设检验
  • 方差分析的基本思想
    • 方差分析（Analysis if Variance）简称ANOVA
    • 检验目的是推断多个总体均数是否相等。
    • 其检验假设为：
    • 方差分析的基本思想就是根据研究设计的类型及研究目的，将总变异分解成两个或多个部分。除随机误差外，其余部分的变异可由某因素的作用来解释，通过比较可能由某因素所致的变异与随机误差的均方（如组内变异），从而了解该因素有无作用。
      • 最终可以通过F检验来回答，总的来说个体总体均数是否相等
    • 以单因素方差分析为例，阐述方差分析的基本思想。
    • 离均差平方和的分解
      • 总变异
        • 三组所有人的载脂蛋白测定值大小不等，此变异成为总变异。
        • 用总离均差平方和SS总 表示。
        • 公式：
          • 体现观测值与总均数的差值
          • 总的自由度=观察例数N-1
      • 组间变异
        • 三组人的载脂蛋白样本均数也大小不等，它们之间的变异称为组间变异。
        • 用组间离均差平方和SS组件 表示。
          • 公式：
            • 体现各样本均数与总均数的差值
            • 组间变异的自由度=组数k-1
        • 组间均方
          • 组间均方MS组间 反映了“血糖”因素的作用（如果确实存在），同时也包含了随机误差（如个体差异和随机测量误差等）。
          • 公式：
      • 组内变异
        • 三组人内部的载脂蛋白也大小不等，这种处理组内部的变异称为组内变异。
        • 用组内离均差平方和SS组内 表示。
          • 公式：
            • 体现观测值减去所在组的样本均数
            • 组内变异的自由度=N-k
        • 组内均方
          • 组内均方MS组内 只反映了载脂蛋白的随机误差，如个体差异和随机测量误差等。
          • 公式：
      • • 总变异可以分解为组间变异和组内变异两个部分
        • 总自由度也分解为组间自由度和组内自由度
    • 检验统计量F
      • • 在H0成立时，F值在理论上应等于1
          • 如果H0成立，即各组总体均数相等，则组间的均方MS组间 只反映了随机误差，跟组内的均方应该是相等的，所以F值在理论上应该等于1
        • 反之，若H1成立时，F值将明显大于1
          • 如果H1成立，即各组总体均数不等或不全相等，则意味着血糖因素是有作用的，此时组间均方不仅包括随机误差，还包括了血糖因素的作用，那么它应该大于组内均方，这时F值将明显大于1
  • 完全随机设计的单因素方差分析
    • 基本原理
      • 适用于只有一个处理因素的完全随机设计， 这个处理因素可以有两个或者两个以上的处理水平。
        • 如前例，只涉及一个研究因素“血糖因素”， “三组人”即为该因素的三个水平。
      • 总变异及总自由度可以分解为：
      • 若检验处理组间是否有差别，统计统计量F为：
      • 例：
        • 方差分析统计结果如图：
    • 均数之间的多重比较
      • 方差分析的F检验，当P≤0.05，按α=0.05，拒绝H0，接受H1，故可以认为各组总体均数不等或不全相等。
      • 想要确定哪些组间有差别，应该进一步地做均数之间的多重比较
      • 注意！在处理组数>2时，均数之间的多重比较若扔用t检验对任意两两均数之间进行比较，则会增大犯第一类错误的概率。
      • 探索性研究
        • 事先不明确要比较哪些组
          • 在进行方差分析的F检验之后，P值小宇0.05，再进行多重比较
        • 方法
          • 多重比较（Multiple Comparisons）
            • 如LSD、Bonferroni、Dunnett方法等。
          • 亚组同质性检验（Homogeneous Subsets)
            • 如SNK、Tukey HSD方法等。
      • 验证性研究
        • 事先就明确了需要进行哪些组间比较
          • 不需要进行方差分析的F检验，可以直接进行组间的多重比较
    • 单因素方差分析的适用条件
      • 各处理组样本来自正态总体（对于正态性要求不严格）；
      • 各样本是相互独立的随机样本；
      • 各处理组的总体方差相等，即方差齐性。
        • 用Levene方法检验是否满足方差齐性假定。
  • 随机区组设计的两因素方差分析
    • 随机区组设计的两因素是指处理因素和区组因素。
      • 令处理因素有k个水平(≥2），区组因素有b个水平（b≥2），即有b个区组，则总例数N=bⅹk。
    • 总变异可以分解为：
    • 总自由度可以分解为：
    • 例：
      • 统计分析结果：处理间P＞0.05，接受H0，认为各处理组无差异（如果结果有差异，则需进一步对各处理组之间进行多重比较）； 区组间P＜0.05说明总的来说区组间有差异，可以进行多重比较。 实际工作中更关心处理因素是否有影响……
      • （纵向因素）处理因素有个水平→k=3
      • （横向因素）区组因素有8个水平→b=8
      • 总例数N=bⅹk=8ⅹ3=24
    • 公式（了解）：
    • 检验处理因素是否有作用
    • 检验区组因素有无作用
    • 注：实际应用中，通常关心处理因素，即处理组间是否有差别； 而对于区组因素，主要是为了减少个体间差异对研究结果的影响，提高统计效率。
  • 方差分析的注意事项
    • 方差分析与t检验的联系
      • 两个独立样本均数比较的t检验，可以用单因素方差分析代替
      • 配对设计的t检验，可以用随机区组设计的两因素方差分析代替
      • 两者的计算结果有如下关系：（或F=t的平方）
        • 二者对应的概率P值完全相等
      • 注意！t检验可以用对应的方差分析来代替；但方差分析却不能用两两的t检验来代替，否则会增大第一类错误的概率！
    • 两种类型的方差分析比较
      • 与完全随机设计的单因素方差分析相比，随机区组设计更容易检验处处理组间的差别，提高了统计效率。
        • 随机区组设计把相似的个体配成了一个区组，减少了个体差异，从而减少了误差，提高了统计效率
        • 验证：把随机区组设计的两因素方差分析的例子用单因素方差分析来做，比较一下它们的方差分析结果有什么关系。
          • 注意随机区则设计的方差分析结果中，区组加上误差的离均差平方和=单因素方差分析的组内变异离均差平方和
            • 说明随机区组设计，区组部分的变异是从单因素方差分析中组内变异中分解出来的，所以通常情况下它的误差要更小，从而提高了统计效率。（类似配对样本t检验与独立样本t检验）
    • 非参数统计
      • 如果不满足参数检验条件，则适宜用非参数检验
        • 指当数据不满足正态性或不满足方差齐性时，经典的方差分析不适用，可考虑非参数检验
        • 最常用秩和检验
      • 完全随机设计的单因素非参数方法→Kruskal-Wallis秩和检验
        • 治愈天数呈偏态分布→采用秩和检验
      • 随机区组设计的两因素非参数方法→Friedman秩和检验
        • 免疫球蛋白呈偏态分布→非参数检验
  • SPSS软件操作
    • 完全随机设计的单因素方差分析
      • 方法一：单因素方差分析
        • • 运行语法
            • 输出窗口查看统计结果
      • 方法二：一般线性单变量分析
        • • 运行语法
            • 输出窗口查看统计结果
      • 两种方法结论完全一致，只是表达形式上会有差别
    • 随机区组设计的两因素方差分析
      • • 运行语法
          • 输出窗口查看统计结果
    • 完全随机设计的单因素非参数方法→Kruskal-Wallis秩和检验
      • • 运行语法
          • 输出窗口查看统计结果
            • 秩就是数据的“名次”。 秩和检验就是不看原始分数多少分，只看这个分数在所有分数里排第几名（即秩），然后把名次加起来做检验的一种统计方法。
    • 随机区组设计的两因素非参数方法→Friedman秩和检验
      • • 运行语法
          • 输出窗口查看统计结果
• 分类变量比较的假设检验
  • 率的抽样误差与总体率的估计
    • 率的抽样误差
      • 定义
        • 在抽样研究中，由于抽样造成的样本率与总体率之间的差异或者样本率之间的差异，称为率的抽样误差（Sampling Erroe，SE）
        • 抽样误差是不可避免的，造成抽样误差的根本原因是个体变异的客观存在。
        • 例：调查某社区儿童家长对基本保健知识的知晓率
          • 从总体中随机抽取两个样本，两个样本含量n都为100。 由于随机抽取，两样本所包含的个体不同，所以两个样本的率通常也不同——P1=45%,P2=50%。 这两个样本率之间的差异称为率的抽样误差。 同样，由于个体的不同，样本率与总体率也是有差异的，这也属于抽样误差。
      • 计算
        • 率的抽样误差大小用率的标准误来衡量。
          • π=总体率 在实际工作中，总体率一般是未知的——需要用样本率来代替。
        • 常得到率的标准误的估计值：
      • 性质
        • 率的标准误，与样本含量的平方根成反比。
        • 实际工作中减少抽样误差的有效方法是增大样本含量。
    • 总体率95%置信区间的估计
      • 定义
        • 根据样本率计算出有（1-α）的把握包含总体率的一个数值范围，这个数值范围称为总体率的置信区间，该（1-α）称为置信度。一般α取0.05，则置信度为95%，即估计总体率95%置信区间。
          • 简单总结定义： 1. 你想知道一个总体的真实比例（总体率 π）。 2. 你只能调查一个样本，得到一个样本比例 (p)。 3. **置信区间：** 根据样本结果 p 计算出来的一个**数值范围**（比如 L - U）。 4. **置信度 (1-α, 常为95%)：** 代表一种**信心/保证程度**——说明如果像你这样抽样调查无数次，其中大约95%次算出来的置信区间，会把这个真实的总体率 π “圈”住。它不是指你的这个具体区间包含 π 的概率是95%（对于具体区间，π要么在里面要么不在）。 5. 结论表达：我们**有95%的把握（信心）认为，总体的真实比例（总体率）介于 [计算出的置信区间下界L] 和 [上界U] 之间**。 --- 回到图片里的例子： > 估计某小学儿童龋患率，抽查150人，龋患60人，p=40%。 > 如果我们计算出的**95%置信区间是 32% - 48%**。 > **结论是：我们有95%的把握认为，该小学全体儿童的真实龋患率在32%到48%之间。
      • 计算
        • 在样本量较小时，可用查表法来估计总体率的置信区间
        • 当n足够大，且样本率p和(1-p)均不太小时，如np与n(1-p)均大于5时，采用正态近似法。总体率95%置信区间为：
          • 子主题
        • 注：置信区间的估计是有概率性的。
          • 有5%的概率有可能犯错误。
  • 独立样本四格表资料的卡方检验
    • 基本原理
      • 例：
        • 关心总体率是否不同：根据样本率不同，不能直接推论出总体率不同，因为存在抽样误差→需要用独立样本比较的卡方检验。
      • 统计量：
      • 检验假设：以两个样本率的比较为例
      • 通用表格形式：
      • 检验目的：推断两个总体率（或构成比）是否相等。
    • 适用条件
      • 当n≥40且T＞5时，Pearson卡方检验
      • 当n≥40且1≤T＜5时，连续性校正卡方检验
      • 当n＜40或T＜1时，Fisher精确概率法
        • 该方法理论依据是超几何分布。按照以下公式直接计算表内四个格子数据的各种组合的概率，然后根据单侧或双侧计算累计概率最后与检验水准α比较，做出是否拒绝H的结论。
        • n为总例数，a、b、c、d分别为四格表中四个格子的实际数，!为阶乘的符号。
  • 配对设计四格表资料的卡方检验
    • 基本原理
      • 例：
      • 通用表格形式：a、d代表两组检查结果一致；c、b代表两组检查结果不一致。
        • 如果关系两组是否有差别，应该重点考察b和c
      • 检验目的：推断两个总体率（或构成比）是否相等。
      • 检验假设：以两个样本率的比较为例
        • B、C是大写的，代表的是总体的频数
      • 统计量：
        • 只跟b和c有关
    • 适用条件
      • 部分医学统计书教材中的观点
        • 当b+c>40，配对设计四格表卡方检验公式：
        • 当b+c≤40，连续性矫正配对设计四格表卡方检验公式：
          • 注：当b+c很小时，由于正态分布不能很好地近似二项分布，所以采用卡方检验是不合理的。
      • SPSS软件中的观点
        • 当b+c≤25，精确概率法。
          • （一般了解）
        • 当b+c>25，校正公式：
  • 多个独立样本行×列表资料的检验
    • 行×列表资料的卡方检验（无序分类变量）
      • 例：
      • 行变量、列变量均为无序分类变量。
      • 检验目的：推断多个总体率（或构成比）是否相等。
      • 检验假设：以多个样本率的比较为例，
        • 类似方差分析。区别在于：方差分析比较的是多个总体均数，卡方检验比较的是多个总体率
      • 统计量：
      • 适用条件
        • 一般认为，行×列表中若有1/5以上格子数的1≤T<5或一个格子的T<1，则不能直接用卡方检验。
          • 推荐：行×列表的精确概率法
      • 注：若多个样本率（或构成比）比较的卡方检验结论为拒绝H0，则只能认为多个总体率（或构成比）之间总的来说有差别，但并不意味着任何两组都有差别。
    • 行×列表资料的假设检验（单项有序分类变量）
      • 行×列表中的分组变量为无序变量，而测量指标为有序分类变量即登记资料。采用非参数的秩和检验。
      • 两个样本的检验
        • 例：
        • 检验目的：推断两组总体分布是否不同
        • 检验假设为：
        • 统计方法：采用两个独立样本的秩和检验（Wilcoxon两样本比较法）
      • 多个样本的检验
        • 例：
      • 检验目的：推断多组总体分布是否不同
      • 检验假设为：
      • 统计方法：采用多个独立样本的秩和检验（Lruskal-Wallis法）
  • SPSS应用
    • 做卡方检验前需要先整理资料！
    • 独立样本四格表资料的卡方检验
      • • 做卡方检验前，需要先加权
          • 运行语法
            • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
              • 卡方检验
                • 运行语法
                  • 输出窗口查看统计结果
    • 连续性校正卡方检验
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • 运行卡方检验语法
              • 输出窗口查看统计结果
    • Fisher精确概率法
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • 运行卡方检验语法
              • 输出窗口查看统计结果
    • 配对设计四格表资料的卡方检验
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • • 运行（麦克尼马尔检验）语法
                • 输出窗口查看
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • 运行（麦克尼马尔检验）语法
              • 输出窗口查看
    • 多个独立样本行×列表资料的检验
      • 行×列表资料的卡方检验（无序分类变量）
        • • 运行加权语法
            • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
              • 运行独立样本四格表卡方检验语法
                • 输出窗口查看统计结果
      • 行×列表资料的假设检验（单项有序分类变量）
        • 采用秩和检验
          • • 运行加权语法
              • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
                • 两个独立样本的秩和检验
                  • 运行语法
                    • 输出窗口查看
          • • 运行加权语法
              • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
                • 多个独立样本的秩和检验
                  • 运行语法
                    • 输出窗口查看
• 直线回归与相关
  • 直线回归
    • 实例
    • 直线回归的概念
      • 直线回归（linear regression）用直线方程表达X和Y之间的数量依存关系。
      • X常作为自变量（independent variable）
      • Y常作为因变量（dependent variable）
    • 直线回归方程的估计
      • 直线回归方差的一般表达式
        • ：是实测值Y的预测值（predicted value），是直线上点的纵坐标。
        • a和b的关系
          • a：是回归直线在Y轴上的截距，即X=0时Y的预测值。
          • b：是回归直线的斜率，又称回归系数。
            • b>0表示Y随增大而增大；
            • b<0表示Y随X增大而减小；
            • b=0表示X与Y无直线关系。
          • b的统计学意义：当X改变一个单位时，Y的预测值平均改变b个单位。
        • b和a的估计
          • 最小二乘法（the method of least aquares，LS)：各实测点到直线的纵向距离的平方和最小。
            • 剩余或残差（residuals） 剩余平方和或残差平方和（sum of squared residuals）
    • 回归系数的假设检验
      • b为样本回归系数，要判断直线回归方程是否成立，需要检验总体回归系数β是否为0.
      • 检验假设为：
        • 只有经过检验P值≤0.05，拒绝H0，接受H1，认为β≠0的时候，才能认为直线回归方程成立。
      • 方法一：方差分析
      • 方法二：t检验
    • 直线回归的应用
      • 预测
        • 的95%置信区间估计
          • 当X=X0时，以95%的概率估计Y（条件）均数的置信区间为
          • 前例中，当中年女性的体重指数为3.50时，预测中年女性的平均收缩压95%置信区间。
        • 个体Y值的95%容许区间估计
          • X=X0时，以95%的概率估计个体Y值的波动范围为
          • 前例中，当某中年女性的体重指数为3.50时，预测其个体收缩压的95%波动范围。
      • 直线回归的使用条件（LINE）
        • 线性：Y与X之间是线性关系（L)
        • 独立性：所有的观测值是相互独立的（I）
        • 正态性：Y服从正态分布（N)
        • 方差齐性：对于所有自变量取值，Y总体方差相等（E)
      • 应用直线回归的注意事项
        • 作回归分析要有实际意义
          • 根据专业知识来决定是否需要作回归直线
        • 只能在建立回归方程时自变量取值范围内预测因变量，不能任意外延。
          • 因为超过自变量的取值范围时，X和Y是否是线性关系，我们是不知道的；即使是线性关系，这种线性关系是否发生了变化也不能确定。
        • 在进行直线回归分析之前，应绘制散点图。
          • 通过散点图可以判断Y与X之间是有线性关系的。
          • 散点图还可以帮助我们发现异常点或突出点，慎重考虑是否需要把它剔除
  • 直线相关
    • 直线相关的概念
      • 直线相关（liner correlation）用于描述具有直线关系的两个变量之间的相互关系。
      • r：相关系数，correlation coefficient，又称为积差相关系数或Pearson相关系数。
      • r用来衡量有直线关系的两个变量之间相关的密切程度和方向。r没有单位，-1≤r≤1.
    • 相关类型
      • 正相关：0<r≤1，X、Y间呈同向变化。
      • 负相关：01≤r<0，X、Y呈反向变化。
      • 零相关：r=0，X、Y间没有线性相关关系
    • 相关系数的估计
    • 相关系数的假设检验
      • r为样本相关系数，要判断两变量之间是否存在相关性，需要检验总体相关系数ρ是否为0.
      • 统计量t
        • 注：只有当ρ≠0时，才能根据|r|的大小判断相关的密切程度。 如果t检验得到的P值＞0.05，即使相关系数|r|再大，也不能认为存在相关性。
    • 直线相关的适用条件
      • 独立性：所有的观测值是相互独立的
      • 正态性：两个变量X、Y服从双变量正态分布（bivariate normal distribution）。
    • 直线回归与相关的区别和联系
      • 区别
        • 意义不同
          • 相关表达两个变量之间相互关系的密切程度和方向。
          • 回归表达两个变量之间的数量依存关系，已知X值可以预测Y值。
        • 资料要求不同
          • 回归要求Y服从正态分布；X是可以精确测量和严格控制的变量，称为Ⅰ型回归。
          • 相关要求X、Y服从双变量正态分布。这种资料若进行回归分析则称为Ⅱ型回归。
      • 联系
        • r与b的符号一致，同正同负
        • r与b的假设检验等价
          • 对应的概率P值是相等的，意味着回归系数的假设检验有统计学意义，则相关系数的假设检验也一定有统计学意义。
        • 可以用回归解释相关
          • r²称为决定系数（coefficient of determination）
            • r²反映了回归平方和占总平方和的比例，其越接近于1，回归直线拟合的效果越好。
  • 秩相关
    • 又称等级相关。主要适用于
      • 不服从双变量正态分布而不宜作直线相关分析。
      • 总体分布类型未知的双变量资料。
      • 原始数据是用等级表示。
    • Spearman等级相关是基于秩次的非参数相关分析。
    • Spearman等级相关系数的估计
    • Spearman等级相关系数的假设检验
      • 其检验假设为：
      • 当样本量较小，可以直接查表
      • 当n>50时，t检验的计算公式为：
    • 应用
  • SPSS软件的应用
    • • • 运行语法，输出窗口查看散点图，双击散点图拟合曲线
          • 线性相关分析
            • 运行语法
              • 输出窗口查看
                • 回数据库查看
    • Spaerman等级相关的应用
      • • 先对数据进行加权
          • 运行语法，查看数据库右下角出现“权重开启”
            • 运行Spearman等级相关的程序
              • 输出窗口查看

医学统计学与SPSS软件基础

• 基本概念与SPSS数据管理
  • 基本概念
    • 统计学（statistics)
      • 运用概率论和数理统计研究数据的收集、整理和分析
      • 医学统计学
        • 统计学应用于医学领域
      • 统计分析
        • 统计描述
        • 统计推断
          • 用已知的样本来推断未知的总体
        • 总体估计
        • 假设检验（重难点）
      • 统计工作的基本步骤
        • 统计设计
        • 搜集资料
        • 整理资料
        • 分析资料
    • 总体(population)
      • 根据研究目的确定的同质观察单位的全体——通常数目庞大
        • 同质——相同性质、共同特征
      • 例：调查某地 1992年 健康 成年男性的身高。（有限总体——有时间和空间的限制）
      • 例：某种药物 治疗 高血压患者 的疗效。（无限总体——没有时间和空间的限制）
    • 样本(sample）
      • 从总体中随机抽取部分观察单位，其实测值的集合
        • 随机抽样……减少偏性，使样本对总体有代表性
        • 随机抽样的目的：用样本信息来推断总体特征（统计推断）
          • 用已知的样本来推断未知的总体——前提：随机抽样
    • 误差
      • 抽样误差——不能避免
      • 随机测量误差——不能避免
      • 系统误差——可以避免
      • 过失误差——可以避免
    • 概率（probabiity）
      • 描述随机事件发生的可能性大小，用P表示
        • 例：某种新药治疗某种疾病的患者300人，治愈了240人，则治愈率为80%（频率）
          • 概率是未知的，在样本量足够大时，频率≈概率
      • 必然事件→P=1
      • 不可能事件→P=0
      • 随机事件→0<P<1
      • 小概率事件
        • 当一个事件的概率P≤0.05或P≤0.01时，称为小概率事件
          • P=0.05代表100次实验中有5次时间发生
        • 特点：某件事发生的可能性很小，在一次试验中基本上是不会发生的
    • 资料的类型
      • 数值变量（NumericalVariable）
        • 又称为定量资料或计量资料，其变量值是定量的，表现为数值大小，一般有度量衡单位
          • 例：血压，身高，体重，血脂等。
        • 数值变量的分布类型
          • 对称分布
            • 集中位置居中，左右两侧频数基本对称。
            • 常见正态分布
              • 正态分布曲线特征
                • 正态分布有两个参数：均数μ和标准差σ。常用N(μ,σ²)。
                  • 均数μ又称为位置参数，决定了曲线的位置：μ越大，曲线越右移。
                  • σ²为变异度参数：σ²越大，曲线越矮胖
              • 正态分布曲线下面积分布规律
                • (μ - σ, μ + σ)→68.27% (μ - 1.96σ, μ + 1.96σ)→95% (μ - 2.58σ, μ + 2.58σ)→99%
              • 标准正态分布
                • 任何正态分布经过标准化变换，都能转化成唯一的标准正态分布
                • 标准正态分布曲线下面积分布规律
          • 偏态分布
            • 集中位置偏向一侧，频数分布不对称。
        • 数值变量的统计描述指标
          • 集中趋势指标的描述
            • 1.算数均数（均数 mean）
              • 适用于正态分布
              • 总体均数：μ；样本均数：x
            • 2.中位数（median,M）
              • 主要适用于偏态分布资料
                • 对于偏态分布资料，中位数只和位置居中的观察值有关，适合描述偏态分布的集中趋势。
              • 中位数是指将一组观察值从小到大排列，位置居中的观察值
              • 例：
              • 对于近似正态分布，中位数和均数是近似相等的。
          • 离散趋势指标的描述
            • 1.极差或全距（range,R）
              • R=最大值-最小值
              • 计算简单，但是不能反映所有变量值的变异程度。
            • 2.方差（Variance,VAR）
              • 表示一组变量值的平均离散程度
              • 方差越大，离散程度越大。
              • • 总体方差通常是未知的
                • 样本方差实际上是用样本均数代替了总体均数
            • 3.标准差（Standard Devication,SD）
              • 也表示一组变量值的平均离散程度
              • 适用于正态分布
              • 医学论文中，标准差比方差更常用
                • 因为标准差的单位和均数的单位是一致的，更方便使用
            • 4.四分位数间距（Quartile,Q）
              • 主要适用于偏态分布资料
              • • P₇₅表示75%的数比它小，25%的数比它大。P₇₅又称上四分位数。
                • P₂₅表示25%的数比它小，75%的数比它大。P₂₅又称下四分位数。
              • 代表中间50%的数据的离散程度或变异程度
                • 不受两端极端数据的影响，较稳定，主要适用于偏态分布资料
              • 可以直接用四分位数表达偏态分布资料的离散趋势，形式如下：（P₂₅，P₇₅）。
          • 补充
            • 几何均数（geometric mean，G）
              • 常适用于一种特殊的偏态分布租赁：对正态分布资料
                • 常见于抗体滴度
            • 变异系数（coefficient of variation,CV）
              • 用于描述数据的相对离散程度
              • • 没有单位
                • CV可以>100%，也可以<100%
              • 在比较多组数据的离散程度时
                • 如果数据的度量衡不一样，此时不能应用标准差，而应该用变异系数
                • 当数据的均数相差悬殊时，也不能用标准差，而应该用变异系数
      • 分类变量 （Categorical Variable)
        • 又称为定性资料，其变量值是定性的，表现为互不相容的类别或属性
          • 无序分类变量（Nominal Variable)
            • 又称为名义变量。包括变量值取无等级顺序的二项分类或多项分类
            • 例：性别、血型等分类指标。
          • 有序分类变量（Ordinal Variable)
            • 又称为等级资料，各类之间有程度的差别，即变量值取有等级顺序的几类
            • 例：临床疗效可以分为痊愈、显效、好转、无效。
        • 分类变量的统计描述指标——相对数（Relative Number）
          • 比（Ratio）
            • 又称相对比。表示两个有关联的指标之比。
            • 例：性别比、BMI、OR、RR……
          • 比例（Proportion）
            • 事物内部各部分所占的比重（又称为构成比）。
            • 要求
              • 分母必须包含分子；
              • 分子、分母是性质相同的指标；
              • 各部分的比例之和为100%。
            • 例：
            • 患病率（Prevalence）
              • 表示在某时点上接受检查的人群中现患病例所占的比例
              • 此指标是比例（Proportion），不是率（Rate）
              • 病死率、有效率、治愈率、患病率……实质上都是比例，并不是真正意义上的率。
          • 率（Rate）
            • 表示单位时间内某事件发生的频率
            • 分子为观察期间内某事件的发生例数
            • 分母为观察人-时（Person-Time)总数，即∑（每个观察单位×观察时间）
            • 发病密度（Incidence Density,ID)
              • 观察期间内某疾病心法病例数/该观察期间内人-时总数
              • 实际应用中也可称为发病率（Incidence Rate）
              • 例：某研究调查45～49岁使用口服避孕药的妇女中乳腺癌的发病情况。此研究中，乳腺癌的新发病例数为9，观察人一年数为2935。则此调查人群中乳腺癌的发病密度为：9/2935=0.00307=307/10万人一年。
          • 注意事项
            • 计算率和比例的分母不宜过小；
              • 分母过小，则得到的相对数不稳定
            • 不能以比例代替率；
            • 多个率不能直接相加求平均。
              • 如需求平均律，应该用总的发生数除以总的观察例数。
      • 不同类型的资料，统计方法不同。
        • 数值变量→t检验、方差分析、回归与相关（符合正态分布的数据）
        • 无序分类变量→卡方检验
        • 有序分类变量→秩和检验
      • 各种类型的资料之间可以相互转化。
        • 例：
    • SPSS应用
      • 数值变量的SPSS统计
        • 作直方图或正态曲线帮助判断数据是正态分布还是偏态分布
          • • 运行语法
              • 在输出窗口查看直方图
            • 如需对另一个变量做直方图，如“alt”。语法快捷方式——复制粘贴本段语法，将"height"修改为“alt”，然后运行修改后的语法
              • 在输出窗口查看另一个变量的直方图
        • 数值变量的统计描述
          • • • 输出窗口查看统计描述 注意！ 根据不同指标的不同分布类型， 选择不同的统计描述指标！
      • 样本分类变量的SPSS统计描述
        • • 运行语法
            • 输出窗口查看统计描述
  • SPSS数据管理
    • 变量标签、变量值标签
    • 排序、拆分
      • 语法执行模式
        • 拆分文件+描述
        • 取消拆分+描述
    • 选择个案
      • • • • • 运行统计描述语法即可得到相应的统计描述结果
        • 取消选择个案
          • • • 运行统计描述语法即可得到相应的统计描述结果
    • 计算变量
      • • • 返回数据库查看新变量
    • 重新编码
      • 能够将数值变量转化为分类变量——统计方法发生对应变化！！
      • • • 在数据窗口即可查看重新编码的变量
• 两组数值变量比较的假设检验
  • 一、 均数的抽样误差
    • 1. 定义
      • 在抽样研究者，由于抽样造成的样本均数与总体均数之间的差异或样本均数之间的差异，称为均数的抽样误差（Sampling Error，SE）
      • 抽样误差是不可避免的
        • 造成抽样误差的根本原因是个体变异的客观存在
    • 2. 例：调查某地1992年健康成年男性的身高
    • 3. 计算
      • 抽样误差的大小，即标准误
      • 标准误也可以称为样本均数的标准差
    • 4. 性质
      • 标准误与标准差成正比，与样本含量的平方根成反比
      • 试剂工作中减少抽样误差的有效方法是增大样本含量
  • 二、 t分布
    • 1. 定义
      • 若从正态分布N(μ,σ²)总体中随机抽取样本含量为n的样本，样本均数也服从正态分布N(μ,σ²)。
        • 服从标准正态分布N(0,1)。
        • 服从自由度ν=n-1的t分布
    • 2. 性质
      • 一组与自由度ν有关的曲线，随着ν增大接近标准正态分布。
        • 自由度决定形态：自由度ν = n - 1（n是样本量 ），不同自由度对应不同t分布曲线。比如ν = 1 时，曲线矮胖，离散程度大；ν = 5 时，曲线更集中，形态随ν变化
        • 趋近标准正态分布：当ν逐渐增大，t分布曲线越来越接近标准正态分布（ν→∞ )时，二者几乎重合 ）。像小样本（ν小）时，t分布更 “保守”，尾部概率比标准正态分布大；大样本下，就可近似用标准正态分布替代t分布做统计推断，体现了样本量对分布形态的影响 。
      • t分布与标准正态分布的区别
        • 标准正态分布是均数为0、标准差为1的一条曲线；而t分布是一组与自由度有关的曲线，并且随着自由度增大，t分布会趋近于标准正态分布。
      • t分布中界值与尾侧面积的关系
        • 当t分布曲线中间包含95%的面积时，两侧的界值称为0.05的t界值，此时外侧尾侧面积之和为0.05
        • 若某个t值的绝对值>0.05的t界值，其对应的尾侧面积之和<0.05
        • 若t值绝对值<0.05的t界值，对应的尾侧面积之和则>0.05
  • 三、 总体均数95%置信区间的估计
    • 1. 定义
      • 根据样本均数，计算出有(1 -α)的把握包含总体均数的数值范围，此范围即总体均数的置信区间 。(1 -α)为置信度，常取α = 0.05，对应 95% 置信度，用于估计总体均数 95% 置信区间。
    • 2. 计算
      • 背景实例
        • 随机抽取某市区 40 例居民膳食调查，人均摄入蛋白质样本均数Xˉ = 62.5g，样本标准差S = 5.6g，估计该市区人均摄入蛋白质总体均数的 95% 置信区间。
      • 计算步骤
  • 四、 假设检验的基本原理
    • 1. 核心概念
      • 检验假设
        • 考虑差异来源的两种可能性：
          • H0（无效假设）：假定样本与总体（或两组样本所代表总体 ）无本质差异，差异由抽样误差导致，如“难产男婴体重均数μ =正常男婴体重均数μ0” 。
          • H1（备择假设）：与H0对立，认为样本与总体（或两组样本 ）存在本质差异，如“难产男婴体重均数≠正常男婴体重均数μ0” ，反映研究者想得到的结论方向（双侧/单侧 ）。
      • 检验水准（α ）
        • 即显著性水准，是判断“是否拒绝H0的界限”，常取(α = 0.05) ，代表“小概率事件”的概率阈值 。
          • P≤0.05→拒绝H0→认为有差别
          • P＞0.05→不拒绝H0→认为无差别
    • 2. 基本逻辑 （小概率原理）
      • 前提：先假设H0成立 （如认为难产男婴与正常男婴体重均数相同 ）。
      • 推理：在H0成立前提下，计算样本统计量（如(t)值 ），判断其对应的概率(P) ：
        • 若P≤ 0.05：说明在H0假设下，出现当前样本情况是小概率事件。依据小概率原理，小概率事件在一次抽样中几乎不发生，故拒绝H0，接受H1 ，认为样本与总体（或两组 ）存在本质差异（如难产男婴体重均数和正常男婴不同 ）。
        • 若P > 0.05 ：说明在H0假设下，当前样本情况属大概率事件，无充分证据拒绝H0，故不拒绝H0 （注意不是“接受(H_0)”，只是暂未找到拒绝证据 ）。
    • 3. 实例关联 （难产男婴体重问题 ）
      • 已知正常男婴出生体重均数μ0= 3.26kg，抽取20名难产男婴样本。通过假设检验判断：若拒绝H0（μ =μ0 ），则认为难产男婴体重均数和正常男婴有差异；若不拒绝H0，则暂认为二者无本质差异（差异由抽样误差引起 ） 。
    • 4. 假设检验的思想贯穿于经典统计
      • 同样适用于方差分析、卡方、相关于回归所设计的假设检验
  • 五、 三种t检验
    • 1. 单样本t检验
      • 实例
        • 已知某地正常男婴出生体重均数(\mu_0 = 3.26kg)，随机抽取20名难产男婴，体重数据：3.5、3.5、3.2、3.5、3.3、3.0、3.3、3.2、3.4、2.7、3.4、3.6、3.5、2.8、3.4、2.9、3.5、3.5、4.0、4.0 ，推断难产男婴体重均数与正常男婴是否不同。
      • 基本原理
        • 用于一个样本均数与已知总体均数μ0的比较。
          • 又称样本均数与已知总体均数比较的t检验
        • 检验目的是推断未知总体均数μ是否等于μ0 。
          • 其检验假设为：
        • 计算公式：
          • 分子为样本均数减去已知总体均数μ0，分母为样本均数的标准误，自由度=n-1
      • 适用条件
        • 正态性
          • 样本对应总体服从正态分布。
          • 当数据偏离正态不是很严重时，t检验仍适用 。
    • 2. 两个独立样本t检验
      • 实例
        • 某医师测得12名正常人、13名病毒性肝炎患者血清转铁蛋白含量（g/L），判断患者与正常人含量有无差异。 正常人数据：2.61、2.71、2.73、2.64、2.68、2.81、2.76、2.55、2.91、2.85、2.71、2.64 患者数据：2.34、2.47、2.22、2.31、2.36、2.38、2.15、2.57、2.19、2.25、2.28、2.31、2.42
          • 正常人和病毒性肝炎患者的血清转铁蛋白含量测量都是独立的，所以是两个独立样本
      • 基本原理
        • 两个独立样本均数对应的总体均数为μ1、μ2，μ1、μ2是未知的。）
        • 检验目的是推断μ1与μ2是否相等。
          • 其检验假设为：
        • 计算公式：
          • 分子为两个样本均数之差， 分母为样本均数差值的标准误。
            • 标准误计算公式了解即可。
      • 适用条件
        • 正态性
          • 两个样本对应的总体分别服从正态分布。
          • 当数据偏离正态不是很严重时，t检验仍适用 。
        • 独立性
          • 两个样本的相互独立的，无关任何关联性
        • 方差齐性
          • 两个样本对应的总体方差相等
          • 用Levene方法检验是否满足方差齐性假定
          • 若违背了方差齐性假定，则常用如下统计方法
            • 校正t检验
            • 先变量变换，满足方差齐性后再行t检验
            • 两个独立样本的秩和检验
    • 3. 配对设计t检验
      • 基本原理
        • 常用于三种情况：
          • 1. 按照某些特征（性别、年龄等）先将两个受试对象配成对子，再对同一对子内两个个体分别给予处理
            • 例：
              • 每一个对子中的两个个体是相似的，按照性别和血清胆固醇水平进行了匹配 这两个样本是相关的，是不独立的！——配对设计与独立样本设计的本质区别。
          • 2. 把同一受试对象分成两部分，再分别给予两种不同处理
          • 3. 对同一受试对象处理前后的比较（自身对照设计）
            • 例：
        • 在配对设计中，设每一对子的两个观测变量为X、Y，差值d=X-Y ，d的样本均数对的应总体均数μ0是未知的。
        • 检验目的是推断μ0是否等于0，用于判断配对处理的效应差异 。
          • 其检验假设为：
        • 计算公式：
          • 分子为差值的样本均数，分母是差值的标准误。自由度=n-1，在这里n是对子数。
      • 适用条件
        • 正态性
          • 差值d对应的总体服从正态分布。
          • 当数据偏离正态不是很严重时，t检验仍适用 。
      • 配对设计t检验的统计效率高于两个独立样本t检验。
        • 把相似的个体配成对子，减少了误差
  • 六、 假设检验的注意事项
    • 1. 假设检验的目的
      • 推断两个总体均数是否相等。
    • 2. 假设检验方法的选择
      • 根据不同的研究设计类型，选择不同的方法。
    • 3. Z检验的应用
      • 实际工作中Z检验用于“总体标准差α未知，但样本量n较大” 的情况
      • Z 检验是 t 检验的近似方法 ，用于统计推断等场景
        • 实际工作中应用较少，一般直接用t检验
    • 4. t检验与置信区间的等价性
      • 单样本的t检验
        • 若接受H0，则样本值与已知总体均数差值的总体均数95%置信区间必包括0.
      • 两个独立样本的t检验
        • 若接受H0，则两独立样本差值的总体均数95%置信区间必包括0.
      • 配对设计的t检验
        • 若接受H0，则配对差值的总体均数95%置信区间必包括0.
    • 5. P值不能反映总体均数差别的大小
      • P值越小，越有把握认为两总体均数不相等。
    • 6. 假设检验的结论具有概率性
      • H0原本正确，但P≤0.05，拒绝H0：第一类错误α
        • 即拒绝了原本正确的
      • H0原本不正确，但P>0.05，不拒绝H0：第二类错误β
        • 即接受了原本错误的
      • α为事先指定的检验水准，β未知
      • α越小，β越大；α越大，β越小
        • 如果要同时减少这两类错误，需要增大样本量
    • 7. 功效（power）
      • 又称检验效能或把握度，是指当两总体确实有差别时，按检验水准α，能够发现两总体间差别的能力，即1-β。
        • 一般我们希望功效至少为0.8，对应的β=0.2
      • 要保证比较高的功效，很重要的条件是具有足够的样本量
        • 只有足够大的样本量，才能够减少二类错误β，保证比较高的功效1-β
    • 8. 专业意义与统计学意义是不同的
      • 差别有统计学意义，并不意味着一定有专业意义。
        • 即使差别非常小，没有专业意义，但有足够大的样本量，我们依然可以得到P<0.05，有差别的结论。
      • 反之，即便差别无统计学意义，但也可能具有专业意义。
        • 当样本量较小时，是有可能出现这种情况的。
    • 9. 参数统计与非参数统计
      • 参数检验
        • 概念：对样本所属的已知分布总体的未知参数进行估计或假设检验的这类统计推断方法。
        • t检验、卡方检验、相关与回归都属于参数统计方法。
      • 非参数检验
        • 概念：并非比较总体参数，而是直接比较分布，是一种不拘泥于总体分布的统计方法，它是通过将样本实际数据排序编秩次后，对秩次进行比较。
        • 若不满足参数检验条件，则适宜用非参数检验。
        • 会损失数据的信息。
          • 如果数据满足参数检验的条件，而采用非参数检验，那么有可能会降低统计检验效能。
        • 最常用秩和检验。
          • 两个独立样本的秩和检验（Wilconxon两样本比较法）
            • 设计类型与独立样本的t检验一样，但其数据服从偏态分布
            • 例：
          • 配对设计差值的符号秩和检验（Wilcoxon配对法）
            • 设计类型与配对设计的t检验一样，但其数据服从偏态分布
            • 例：
  • 七、 SPSS的应用
    • 单样本t检验
      • • 打开语法窗口运行语法
          • 输出窗口查看统计描述结果
    • 独立样本t检验
      • • 打开语法窗口运行语法
          • 输出窗口查看统计描述结果
    • 配对t检验
      • • 语法窗口运行语法
          • 输出窗口查看统计描述结果
    • 秩和检验
      • • 运行语法
          • 查看统计结果
    • 配对秩和检验
      • • 运行语法
          • 查看统计结果
• 多组数值变量比较的假设检验
  • 方差分析的基本思想
    • 方差分析（Analysis if Variance）简称ANOVA
    • 检验目的是推断多个总体均数是否相等。
    • 其检验假设为：
    • 方差分析的基本思想就是根据研究设计的类型及研究目的，将总变异分解成两个或多个部分。除随机误差外，其余部分的变异可由某因素的作用来解释，通过比较可能由某因素所致的变异与随机误差的均方（如组内变异），从而了解该因素有无作用。
      • 最终可以通过F检验来回答，总的来说个体总体均数是否相等
    • 以单因素方差分析为例，阐述方差分析的基本思想。
    • 离均差平方和的分解
      • 总变异
        • 三组所有人的载脂蛋白测定值大小不等，此变异成为总变异。
        • 用总离均差平方和SS总 表示。
        • 公式：
          • 体现观测值与总均数的差值
          • 总的自由度=观察例数N-1
      • 组间变异
        • 三组人的载脂蛋白样本均数也大小不等，它们之间的变异称为组间变异。
        • 用组间离均差平方和SS组件 表示。
          • 公式：
            • 体现各样本均数与总均数的差值
            • 组间变异的自由度=组数k-1
        • 组间均方
          • 组间均方MS组间 反映了“血糖”因素的作用（如果确实存在），同时也包含了随机误差（如个体差异和随机测量误差等）。
          • 公式：
      • 组内变异
        • 三组人内部的载脂蛋白也大小不等，这种处理组内部的变异称为组内变异。
        • 用组内离均差平方和SS组内 表示。
          • 公式：
            • 体现观测值减去所在组的样本均数
            • 组内变异的自由度=N-k
        • 组内均方
          • 组内均方MS组内 只反映了载脂蛋白的随机误差，如个体差异和随机测量误差等。
          • 公式：
      • • 总变异可以分解为组间变异和组内变异两个部分
        • 总自由度也分解为组间自由度和组内自由度
    • 检验统计量F
      • • 在H0成立时，F值在理论上应等于1
          • 如果H0成立，即各组总体均数相等，则组间的均方MS组间 只反映了随机误差，跟组内的均方应该是相等的，所以F值在理论上应该等于1
        • 反之，若H1成立时，F值将明显大于1
          • 如果H1成立，即各组总体均数不等或不全相等，则意味着血糖因素是有作用的，此时组间均方不仅包括随机误差，还包括了血糖因素的作用，那么它应该大于组内均方，这时F值将明显大于1
  • 完全随机设计的单因素方差分析
    • 基本原理
      • 适用于只有一个处理因素的完全随机设计， 这个处理因素可以有两个或者两个以上的处理水平。
        • 如前例，只涉及一个研究因素“血糖因素”， “三组人”即为该因素的三个水平。
      • 总变异及总自由度可以分解为：
      • 若检验处理组间是否有差别，统计统计量F为：
      • 例：
        • 方差分析统计结果如图：
    • 均数之间的多重比较
      • 方差分析的F检验，当P≤0.05，按α=0.05，拒绝H0，接受H1，故可以认为各组总体均数不等或不全相等。
      • 想要确定哪些组间有差别，应该进一步地做均数之间的多重比较
      • 注意！在处理组数>2时，均数之间的多重比较若扔用t检验对任意两两均数之间进行比较，则会增大犯第一类错误的概率。
      • 探索性研究
        • 事先不明确要比较哪些组
          • 在进行方差分析的F检验之后，P值小宇0.05，再进行多重比较
        • 方法
          • 多重比较（Multiple Comparisons）
            • 如LSD、Bonferroni、Dunnett方法等。
          • 亚组同质性检验（Homogeneous Subsets)
            • 如SNK、Tukey HSD方法等。
      • 验证性研究
        • 事先就明确了需要进行哪些组间比较
          • 不需要进行方差分析的F检验，可以直接进行组间的多重比较
    • 单因素方差分析的适用条件
      • 各处理组样本来自正态总体（对于正态性要求不严格）；
      • 各样本是相互独立的随机样本；
      • 各处理组的总体方差相等，即方差齐性。
        • 用Levene方法检验是否满足方差齐性假定。
  • 随机区组设计的两因素方差分析
    • 随机区组设计的两因素是指处理因素和区组因素。
      • 令处理因素有k个水平(≥2），区组因素有b个水平（b≥2），即有b个区组，则总例数N=bⅹk。
    • 总变异可以分解为：
    • 总自由度可以分解为：
    • 例：
      • 统计分析结果：处理间P＞0.05，接受H0，认为各处理组无差异（如果结果有差异，则需进一步对各处理组之间进行多重比较）； 区组间P＜0.05说明总的来说区组间有差异，可以进行多重比较。 实际工作中更关心处理因素是否有影响……
      • （纵向因素）处理因素有个水平→k=3
      • （横向因素）区组因素有8个水平→b=8
      • 总例数N=bⅹk=8ⅹ3=24
    • 公式（了解）：
    • 检验处理因素是否有作用
    • 检验区组因素有无作用
    • 注：实际应用中，通常关心处理因素，即处理组间是否有差别； 而对于区组因素，主要是为了减少个体间差异对研究结果的影响，提高统计效率。
  • 方差分析的注意事项
    • 方差分析与t检验的联系
      • 两个独立样本均数比较的t检验，可以用单因素方差分析代替
      • 配对设计的t检验，可以用随机区组设计的两因素方差分析代替
      • 两者的计算结果有如下关系：（或F=t的平方）
        • 二者对应的概率P值完全相等
      • 注意！t检验可以用对应的方差分析来代替；但方差分析却不能用两两的t检验来代替，否则会增大第一类错误的概率！
    • 两种类型的方差分析比较
      • 与完全随机设计的单因素方差分析相比，随机区组设计更容易检验处处理组间的差别，提高了统计效率。
        • 随机区组设计把相似的个体配成了一个区组，减少了个体差异，从而减少了误差，提高了统计效率
        • 验证：把随机区组设计的两因素方差分析的例子用单因素方差分析来做，比较一下它们的方差分析结果有什么关系。
          • 注意随机区则设计的方差分析结果中，区组加上误差的离均差平方和=单因素方差分析的组内变异离均差平方和
            • 说明随机区组设计，区组部分的变异是从单因素方差分析中组内变异中分解出来的，所以通常情况下它的误差要更小，从而提高了统计效率。（类似配对样本t检验与独立样本t检验）
    • 非参数统计
      • 如果不满足参数检验条件，则适宜用非参数检验
        • 指当数据不满足正态性或不满足方差齐性时，经典的方差分析不适用，可考虑非参数检验
        • 最常用秩和检验
      • 完全随机设计的单因素非参数方法→Kruskal-Wallis秩和检验
        • 治愈天数呈偏态分布→采用秩和检验
      • 随机区组设计的两因素非参数方法→Friedman秩和检验
        • 免疫球蛋白呈偏态分布→非参数检验
  • SPSS软件操作
    • 完全随机设计的单因素方差分析
      • 方法一：单因素方差分析
        • • 运行语法
            • 输出窗口查看统计结果
      • 方法二：一般线性单变量分析
        • • 运行语法
            • 输出窗口查看统计结果
      • 两种方法结论完全一致，只是表达形式上会有差别
    • 随机区组设计的两因素方差分析
      • • 运行语法
          • 输出窗口查看统计结果
    • 完全随机设计的单因素非参数方法→Kruskal-Wallis秩和检验
      • • 运行语法
          • 输出窗口查看统计结果
            • 秩就是数据的“名次”。 秩和检验就是不看原始分数多少分，只看这个分数在所有分数里排第几名（即秩），然后把名次加起来做检验的一种统计方法。
    • 随机区组设计的两因素非参数方法→Friedman秩和检验
      • • 运行语法
          • 输出窗口查看统计结果
• 分类变量比较的假设检验
  • 率的抽样误差与总体率的估计
    • 率的抽样误差
      • 定义
        • 在抽样研究中，由于抽样造成的样本率与总体率之间的差异或者样本率之间的差异，称为率的抽样误差（Sampling Erroe，SE）
        • 抽样误差是不可避免的，造成抽样误差的根本原因是个体变异的客观存在。
        • 例：调查某社区儿童家长对基本保健知识的知晓率
          • 从总体中随机抽取两个样本，两个样本含量n都为100。 由于随机抽取，两样本所包含的个体不同，所以两个样本的率通常也不同——P1=45%,P2=50%。 这两个样本率之间的差异称为率的抽样误差。 同样，由于个体的不同，样本率与总体率也是有差异的，这也属于抽样误差。
      • 计算
        • 率的抽样误差大小用率的标准误来衡量。
          • π=总体率 在实际工作中，总体率一般是未知的——需要用样本率来代替。
        • 常得到率的标准误的估计值：
      • 性质
        • 率的标准误，与样本含量的平方根成反比。
        • 实际工作中减少抽样误差的有效方法是增大样本含量。
    • 总体率95%置信区间的估计
      • 定义
        • 根据样本率计算出有（1-α）的把握包含总体率的一个数值范围，这个数值范围称为总体率的置信区间，该（1-α）称为置信度。一般α取0.05，则置信度为95%，即估计总体率95%置信区间。
          • 简单总结定义： 1. 你想知道一个总体的真实比例（总体率 π）。 2. 你只能调查一个样本，得到一个样本比例 (p)。 3. **置信区间：** 根据样本结果 p 计算出来的一个**数值范围**（比如 L - U）。 4. **置信度 (1-α, 常为95%)：** 代表一种**信心/保证程度**——说明如果像你这样抽样调查无数次，其中大约95%次算出来的置信区间，会把这个真实的总体率 π “圈”住。它不是指你的这个具体区间包含 π 的概率是95%（对于具体区间，π要么在里面要么不在）。 5. 结论表达：我们**有95%的把握（信心）认为，总体的真实比例（总体率）介于 [计算出的置信区间下界L] 和 [上界U] 之间**。 --- 回到图片里的例子： > 估计某小学儿童龋患率，抽查150人，龋患60人，p=40%。 > 如果我们计算出的**95%置信区间是 32% - 48%**。 > **结论是：我们有95%的把握认为，该小学全体儿童的真实龋患率在32%到48%之间。
      • 计算
        • 在样本量较小时，可用查表法来估计总体率的置信区间
        • 当n足够大，且样本率p和(1-p)均不太小时，如np与n(1-p)均大于5时，采用正态近似法。总体率95%置信区间为：
          • 子主题
        • 注：置信区间的估计是有概率性的。
          • 有5%的概率有可能犯错误。
  • 独立样本四格表资料的卡方检验
    • 基本原理
      • 例：
        • 关心总体率是否不同：根据样本率不同，不能直接推论出总体率不同，因为存在抽样误差→需要用独立样本比较的卡方检验。
      • 统计量：
      • 检验假设：以两个样本率的比较为例
      • 通用表格形式：
      • 检验目的：推断两个总体率（或构成比）是否相等。
    • 适用条件
      • 当n≥40且T＞5时，Pearson卡方检验
      • 当n≥40且1≤T＜5时，连续性校正卡方检验
      • 当n＜40或T＜1时，Fisher精确概率法
        • 该方法理论依据是超几何分布。按照以下公式直接计算表内四个格子数据的各种组合的概率，然后根据单侧或双侧计算累计概率最后与检验水准α比较，做出是否拒绝H的结论。
        • n为总例数，a、b、c、d分别为四格表中四个格子的实际数，!为阶乘的符号。
  • 配对设计四格表资料的卡方检验
    • 基本原理
      • 例：
      • 通用表格形式：a、d代表两组检查结果一致；c、b代表两组检查结果不一致。
        • 如果关系两组是否有差别，应该重点考察b和c
      • 检验目的：推断两个总体率（或构成比）是否相等。
      • 检验假设：以两个样本率的比较为例
        • B、C是大写的，代表的是总体的频数
      • 统计量：
        • 只跟b和c有关
    • 适用条件
      • 部分医学统计书教材中的观点
        • 当b+c>40，配对设计四格表卡方检验公式：
        • 当b+c≤40，连续性矫正配对设计四格表卡方检验公式：
          • 注：当b+c很小时，由于正态分布不能很好地近似二项分布，所以采用卡方检验是不合理的。
      • SPSS软件中的观点
        • 当b+c≤25，精确概率法。
          • （一般了解）
        • 当b+c>25，校正公式：
  • 多个独立样本行×列表资料的检验
    • 行×列表资料的卡方检验（无序分类变量）
      • 例：
      • 行变量、列变量均为无序分类变量。
      • 检验目的：推断多个总体率（或构成比）是否相等。
      • 检验假设：以多个样本率的比较为例，
        • 类似方差分析。区别在于：方差分析比较的是多个总体均数，卡方检验比较的是多个总体率
      • 统计量：
      • 适用条件
        • 一般认为，行×列表中若有1/5以上格子数的1≤T<5或一个格子的T<1，则不能直接用卡方检验。
          • 推荐：行×列表的精确概率法
      • 注：若多个样本率（或构成比）比较的卡方检验结论为拒绝H0，则只能认为多个总体率（或构成比）之间总的来说有差别，但并不意味着任何两组都有差别。
    • 行×列表资料的假设检验（单项有序分类变量）
      • 行×列表中的分组变量为无序变量，而测量指标为有序分类变量即登记资料。采用非参数的秩和检验。
      • 两个样本的检验
        • 例：
        • 检验目的：推断两组总体分布是否不同
        • 检验假设为：
        • 统计方法：采用两个独立样本的秩和检验（Wilcoxon两样本比较法）
      • 多个样本的检验
        • 例：
      • 检验目的：推断多组总体分布是否不同
      • 检验假设为：
      • 统计方法：采用多个独立样本的秩和检验（Lruskal-Wallis法）
  • SPSS应用
    • 做卡方检验前需要先整理资料！
    • 独立样本四格表资料的卡方检验
      • • 做卡方检验前，需要先加权
          • 运行语法
            • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
              • 卡方检验
                • 运行语法
                  • 输出窗口查看统计结果
    • 连续性校正卡方检验
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • 运行卡方检验语法
              • 输出窗口查看统计结果
    • Fisher精确概率法
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • 运行卡方检验语法
              • 输出窗口查看统计结果
    • 配对设计四格表资料的卡方检验
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • • 运行（麦克尼马尔检验）语法
                • 输出窗口查看
      • • 运行加权语法
          • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
            • 运行（麦克尼马尔检验）语法
              • 输出窗口查看
    • 多个独立样本行×列表资料的检验
      • 行×列表资料的卡方检验（无序分类变量）
        • • 运行加权语法
            • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
              • 运行独立样本四格表卡方检验语法
                • 输出窗口查看统计结果
      • 行×列表资料的假设检验（单项有序分类变量）
        • 采用秩和检验
          • • 运行加权语法
              • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
                • 两个独立样本的秩和检验
                  • 运行语法
                    • 输出窗口查看
          • • 运行加权语法
              • 数据库右下角出现“权重开启”→代表数据处于加权状态→可以做卡方检验
                • 多个独立样本的秩和检验
                  • 运行语法
                    • 输出窗口查看
• 直线回归与相关
  • 直线回归
    • 实例
    • 直线回归的概念
      • 直线回归（linear regression）用直线方程表达X和Y之间的数量依存关系。
      • X常作为自变量（independent variable）
      • Y常作为因变量（dependent variable）
    • 直线回归方程的估计
      • 直线回归方差的一般表达式
        • ：是实测值Y的预测值（predicted value），是直线上点的纵坐标。
        • a和b的关系
          • a：是回归直线在Y轴上的截距，即X=0时Y的预测值。
          • b：是回归直线的斜率，又称回归系数。
            • b>0表示Y随增大而增大；
            • b<0表示Y随X增大而减小；
            • b=0表示X与Y无直线关系。
          • b的统计学意义：当X改变一个单位时，Y的预测值平均改变b个单位。
        • b和a的估计
          • 最小二乘法（the method of least aquares，LS)：各实测点到直线的纵向距离的平方和最小。
            • 剩余或残差（residuals） 剩余平方和或残差平方和（sum of squared residuals）
    • 回归系数的假设检验
      • b为样本回归系数，要判断直线回归方程是否成立，需要检验总体回归系数β是否为0.
      • 检验假设为：
        • 只有经过检验P值≤0.05，拒绝H0，接受H1，认为β≠0的时候，才能认为直线回归方程成立。
      • 方法一：方差分析
      • 方法二：t检验
    • 直线回归的应用
      • 预测
        • 的95%置信区间估计
          • 当X=X0时，以95%的概率估计Y（条件）均数的置信区间为
          • 前例中，当中年女性的体重指数为3.50时，预测中年女性的平均收缩压95%置信区间。
        • 个体Y值的95%容许区间估计
          • X=X0时，以95%的概率估计个体Y值的波动范围为
          • 前例中，当某中年女性的体重指数为3.50时，预测其个体收缩压的95%波动范围。
      • 直线回归的使用条件（LINE）
        • 线性：Y与X之间是线性关系（L)
        • 独立性：所有的观测值是相互独立的（I）
        • 正态性：Y服从正态分布（N)
        • 方差齐性：对于所有自变量取值，Y总体方差相等（E)
      • 应用直线回归的注意事项
        • 作回归分析要有实际意义
          • 根据专业知识来决定是否需要作回归直线
        • 只能在建立回归方程时自变量取值范围内预测因变量，不能任意外延。
          • 因为超过自变量的取值范围时，X和Y是否是线性关系，我们是不知道的；即使是线性关系，这种线性关系是否发生了变化也不能确定。
        • 在进行直线回归分析之前，应绘制散点图。
          • 通过散点图可以判断Y与X之间是有线性关系的。
          • 散点图还可以帮助我们发现异常点或突出点，慎重考虑是否需要把它剔除
  • 直线相关
    • 直线相关的概念
      • 直线相关（liner correlation）用于描述具有直线关系的两个变量之间的相互关系。
      • r：相关系数，correlation coefficient，又称为积差相关系数或Pearson相关系数。
      • r用来衡量有直线关系的两个变量之间相关的密切程度和方向。r没有单位，-1≤r≤1.
    • 相关类型
      • 正相关：0<r≤1，X、Y间呈同向变化。
      • 负相关：01≤r<0，X、Y呈反向变化。
      • 零相关：r=0，X、Y间没有线性相关关系
    • 相关系数的估计
    • 相关系数的假设检验
      • r为样本相关系数，要判断两变量之间是否存在相关性，需要检验总体相关系数ρ是否为0.
      • 统计量t
        • 注：只有当ρ≠0时，才能根据|r|的大小判断相关的密切程度。 如果t检验得到的P值＞0.05，即使相关系数|r|再大，也不能认为存在相关性。
    • 直线相关的适用条件
      • 独立性：所有的观测值是相互独立的
      • 正态性：两个变量X、Y服从双变量正态分布（bivariate normal distribution）。
    • 直线回归与相关的区别和联系
      • 区别
        • 意义不同
          • 相关表达两个变量之间相互关系的密切程度和方向。
          • 回归表达两个变量之间的数量依存关系，已知X值可以预测Y值。
        • 资料要求不同
          • 回归要求Y服从正态分布；X是可以精确测量和严格控制的变量，称为Ⅰ型回归。
          • 相关要求X、Y服从双变量正态分布。这种资料若进行回归分析则称为Ⅱ型回归。
      • 联系
        • r与b的符号一致，同正同负
        • r与b的假设检验等价
          • 对应的概率P值是相等的，意味着回归系数的假设检验有统计学意义，则相关系数的假设检验也一定有统计学意义。
        • 可以用回归解释相关
          • r²称为决定系数（coefficient of determination）
            • r²反映了回归平方和占总平方和的比例，其越接近于1，回归直线拟合的效果越好。
  • 秩相关
    • 又称等级相关。主要适用于
      • 不服从双变量正态分布而不宜作直线相关分析。
      • 总体分布类型未知的双变量资料。
      • 原始数据是用等级表示。
    • Spearman等级相关是基于秩次的非参数相关分析。
    • Spearman等级相关系数的估计
    • Spearman等级相关系数的假设检验
      • 其检验假设为：
      • 当样本量较小，可以直接查表
      • 当n>50时，t检验的计算公式为：
    • 应用
  • SPSS软件的应用
    • • • 运行语法，输出窗口查看散点图，双击散点图拟合曲线
          • 线性相关分析
            • 运行语法
              • 输出窗口查看
                • 回数据库查看
    • Spaerman等级相关的应用
      • • 先对数据进行加权
          • 运行语法，查看数据库右下角出现“权重开启”
            • 运行Spearman等级相关的程序
              • 输出窗口查看