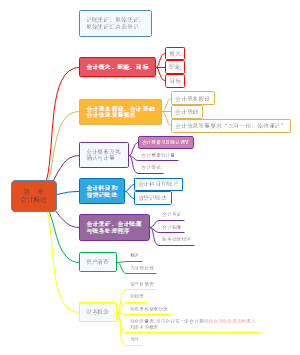
经济师 经济基础知识（中级）

“ 第一章 市场 供给 市第 一场 部需 分 供 经给 济 学与 基 础均 消费者对某种商品或服务愿意而且能够购买的数量 市场需求是消费者需求的总和 两因素:①购买欲望②支付能力两者缺一不可 2012 年经济师考试经济基础知识重点

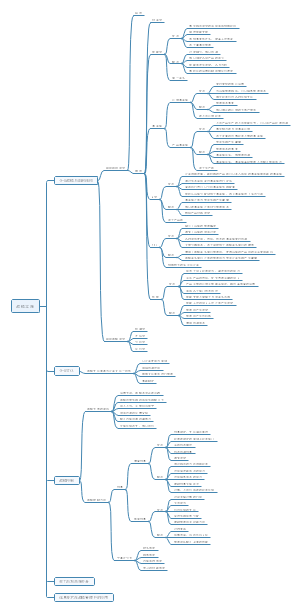
第四部分 统计

• 第二十三章 统计与数据科学
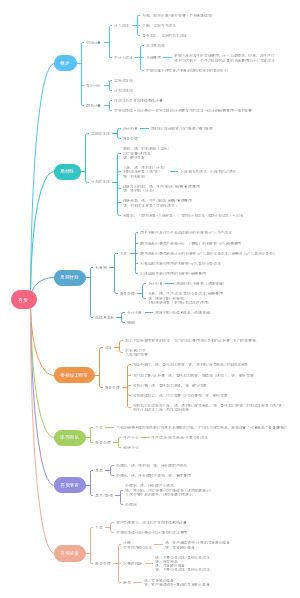
  • 一、统计学 收集、整理、分析数据和从数据中得到结论
    • 描述统计：研究数据收集、整理和描述的统计学方法，其内容包括： 1.如何取得所需要的数据 2.如何用图表或数学方法对数据进行整理和展示 3.如何描述数据的一般特征
    • 推断统计：研究利用样本数据来推断总体特征的统计方法，其内容包括： 1.参数估计：利用样本信息推断总体特征 2.假设检验：利用样本信息判断对总体假设是否成立
  • 二、变量和数据
    • 变量：研究对象的属性或特征，变量可以有两个或更多个可能的取值
      • 定量（数量）变量：变量的取值是数量，如企业销售额、注册员工数
      • 定性变量：分类变量和顺序变量 1.分类变量：定量的取值是类别，如企业所属行业、员工性别 2.顺序变量：定量的取值是类别且有顺序，如员工受教育水平
    • 数据：是对变量进行测量、观测的结果，数据可以是数值、文字或图像等形式
  • 三、数据的来源
    • 按收集方法： 1.观测数据：通过直接调查或测量而收集的数据，几乎所有与社会经济现象有关的统计数据都是观测数据，如GDP、CPI、房价等 2.实验数据：通过实验中控制实验对象以及其所处的实验环境收集到的数据，如一种产品的使用寿命数据
    • 按来源分类： 1.一手数据：来源于调查和科学实验所得来的数据 2.二手数据：来源于别人调查或实验的数据
  • 四、统计调查 有计划收集数据信息资料的过程
    • 按调查对象的范围不同分类： 1.全面调查：全面统计报表和普查，如经济普查的对象是中华人民共和国境内从事第二、三产业活动的全部法人单位、产 业活动单位和个体经营户 2.非全面调查：非全面统计报表、抽样调查、重点调查和典型调查
      • 全面调查涉及面广、耗费人财力大 在不影响调查目的情况下，通常采用非全面调查
    • 按调查登记的时间是否连续分类： 1.连续调查：现象在一年内的数量变化，如工厂的产品生产、原材料的投入、能源的 消耗、人口的出生、死亡等 2.非连续调查：一定时间点上的状态研究，如生产设备拥有量、耕地面积等
    • 统计调查的方式包括：统计报表、普查、抽样调查、重点调查和典型调查 1.统计报表：统一表式、统一指标、统一报送时间和报送程序（重要方式） 2.普查：为某一特定目的而专门组织的一次性调查，主要用于收集处于某一规定时点状态上的社会经济现象的基本全貌（适用范围较窄） 3.抽样调查：随机抽取一部分作为样本进行调查，并根据结果来推断总体特征（经济性、时效性、适应性、准确性） 4.重点调查：选择少数标志性总体中占比较大的重点单位进行调查，如中国城市指标调查 5.典型调查：选择若干具有意义的或有代表性的单位进行调查来弥补不足：如普查后的典型数据再调查
  • 五、数据科学与大数据
    • 数据科学：通过系统性研究获取与数据相关的知识体系的学科
    • 大数据：在一定时间内，利用新处理模式具有决策、发现、优化能力的海量、高增长率和多样化的信息信息资产 ”4V“：数据量大、数据多样性、价值密度低、数据产生和处理速度快
    • 数据挖掘：从大量实际应用数据中，提取有潜在价值的信息和知识的过程
• 第二十四章 描述统计
  • 一、集中趋势的测度：指一组数据向某一中心值靠拢的倾向，测度集中趋势也就是寻找数据一般水平的代表值或中心值
    • 1.均值（平均数）：数据组中所有数值的总和除以该组数值的个数 （数值数据、受极端值影响） 2.中位数：一组数据从小到大或从大到小的顺序进行排列，位置居中的数值 （顺序数据、数值数据、不受极端值影响） 3.众数：一组数据中出现次数（频数）最多的变量值 （分类数据、顺序数据、不受极端值影响）
  • 二、离散程度的测度 反映数据之间的差异程度
    • 1.方差：数据组中各数值与其均值离差平方的平均数（方差越小，距离越小，均值代表性越好） 2.标准差：方差的平方根，度量数值与均值的平均距离（方差越小，距离越小，均值代表性越好） 注：不能直接用标准差比较不同变量的离散程度 3.离散系数（变异系数/标准差系数）：标准差与均值的比值，消除了测度单位和观测值水平不同的影 响 ， 可以直接用来比较变量的离散程度
  • 三、分布形态的测度
    • 1.偏度系数：数据分布的偏斜方向和程度，描述的是数据分布对称程度（测量数据分布偏度的统计量） 2.标准分数：统计上常用的一种标准化方法，给定了数值距离均值的相对位置
  • 四、变量间的相关分析
    • 按相关程度划分： 1.完全相关：一 个变量的取值变化完全由另一个变量的取值变化所确定 2.不完全相关：两个变量之间的关系介于完全相关和不相关之间 3.不相关：两个变量的取值变化彼此互不影响
    • 按相关方向划分： 1.正相关：一个变量的取值由小变大，另一个变量的取值也相应的由小变大 (同方向变化) 2.负相关：一个变量的取值由小变大，另一个变量的取值由大变小(反方向变化)
    • 按相关形式划分： 1.线性相关：两个相关变量之间的关系大致呈现线性关系 2.非线性相关：两个相关变量之间的关系近似于某种曲线方程的关系
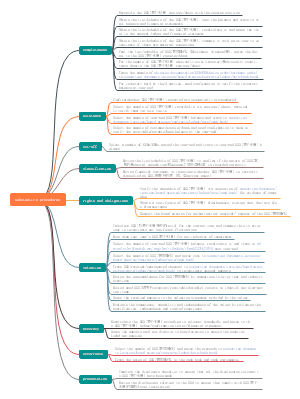
• 第二十五章 抽样调查
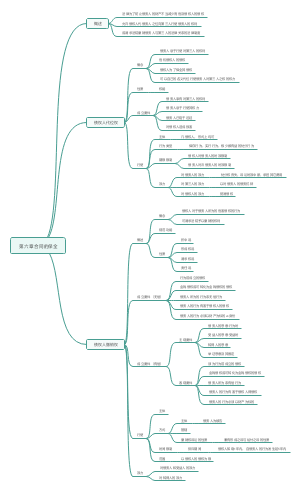
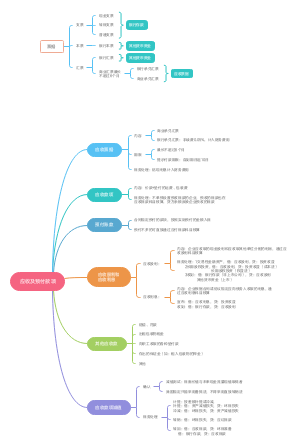
  • 一、抽样调查基本概念 使用频率最高的调查方式
    • 基本概念
      • 1.总体：调查对象的全体 2.样本：总体的一部分，从总体中按一定原则抽取的部分个体所组成，是一个集合 3.总体参数：总体指标值，它是未知的常数，根据总体中所有单位的数值计算，常用的参数有总体总量、总体均值、总体比例、总体方差等 4.样本统计量（估计量）：根据样本中各单位的数值计算，是对总计参数的估计，是一个随机变量，常用的样本统计量有样本均值、样本比例、 样本方差，如：抽中的 2000 家企业中 有对外合作意向的企业 5.抽样框：抽样总体的具体表现，如电话薄、人员名册
    • 根据抽取样本方法划分
      • 概率（随机）抽样：1.按一定概率以随机原则抽取样本；2.总体中每个单元被抽中的概率是已知的或可计算的；3.进行估计时要考虑每个单元被抽中概率
        • 具体方式：1.简单随机抽样；2.分层抽样；3.系统抽样；4.整群抽样；5.多阶段抽样
      • 非概率（非随机）抽样：根据方便或主管判断抽取样本的方法，主要特征是抽取样本时并不是依据随机原则
        • 具体方式：1.判断抽样；2.方便抽样；3.自愿样本；4.配额抽样
    • 抽样调查的一般步骤：1.确定调查问题；2.调查方案设计；3.实施调查过程；4.数据处理分析；5.撰写调查报告
    • 抽样调查中的误差
      • 抽样误差：由于抽样的随机性造成的，样本统计量估计总体参数时出现的误差
      • 非抽样误差：除抽样误差以外，由其他原因引起的样本呢统计量与总体真值之间的差距 1.抽样框误差：样本框不完善造成的 2.无回答误差：调查人员没能够从被调查者那里得到所需要或真实的数据 3.计量误差：由于调查所获得的数据与其真值之间不一致造成的误差
  • 二、几种基本概率抽样方法
    • 简单随机抽样：放回简单随机抽样和不放回简单（只抽一次）随机抽样，适用于①抽样框中没有更多可以利用的辅助信息；②调查对象分布的范围不广阔；③个体之间的差异不大
    • 分层抽样：先把总体分为不同层，再在不同层内独立、随机抽取样本，得到分层样本，适用于：抽样框中有足够的辅助信息，能够将总体单位按某种标准划分到各层之中，实现同一层各单位差异尽可能小，不同层差异尽可能大
    • 系统抽样：将总体中的所有单元按顺序排列，在规定范围内随机抽取一个初始单元，然后按事先规定的规则抽取其他样本单元，适用于：对抽样框的要求比较简单，只要求总体单位按一定顺序排列（系统抽样的估计效果与总体排列顺序有关）
    • 整群抽样：将总体中所有的基本单位按照一定规则划分为互不重叠的群 ，抽样时直接抽取群，对抽中的群调查其基本单位，对没有抽中的群则不进行调查，适用于：对某些特殊群结构进行调查
    • 多阶段抽样：一次抽取到最终样本单位很难实现，往往需要经过两个及两个以上抽样阶段，适用于在大范围中的抽样调查
  • 三、估计量和样本量
    • 估计量的性质：①一致性；②无偏性；③有效性
    • 抽样误差的估计：抽样调查是无法避免的，但可计算： 1.抽样误差与总体分布有关 ，总体单位值之间差异越大， 即总体方差越大，抽样误差越大 2.抽样误差与样本量n有关 ，其他条件相同，样本量越大，抽样误差越小 3.抽样误差与抽样方式和估计量的选择也有关，如分层抽样的估计量方差一般小于简单随机抽样 4. 利用有效辅助信息的估计量也可以有效的减小抽样误差
    • 样本量的确定应考虑的因素：1.调查的精度；2.总体的离散程度；3.总体的规模；4.无回答情况；5.经费的制约；6.调查的限定时间、实施调查的人力资源等
• 第二十六章 回归分析
  • 一、回归分析 根据相关关系的具体形态，选择一个合适的数学模型 ，来近似的表达变量间的平均变化关系
    • 回归分析分为一元回归模型和多元回归模型 回归分析时，首先需要确定因变量和自变量。 回归分析中，被预测或被解释的变量称为因变量用Y 表示； 用来预测或解释因变量的变量称为自变量，一般用 X 表示 回归分析重要应用就是预测，即利用估计的回归模型预测因变量数值
    • 回归分析与相关分析的关系： 1.联系：具有共同的研究对象，互相补充 2.区别：回归分析研究变量之间相关关系的具体形式；相关分析研究变量之间相关方向和相关程度
  • 二、最小二乘法：使因变量的观测值与估计值之间的离差 (残差) 平方和最小来估计数值的方法
  • 三、决定系数（R2）：测量回归直线对样本数据的拟合（因变量能力）程度，数值越高，拟合效果越好
• 第二十七章 时间序列分析
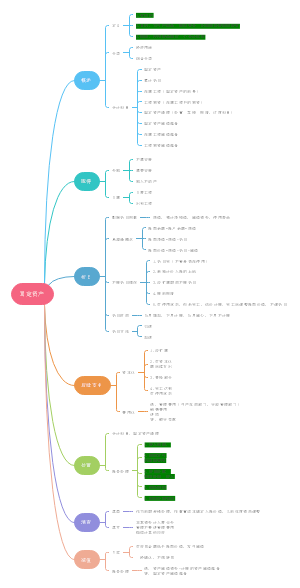
  • 一、时间序列及其分类 某一指标数值按先后顺序编制形成的序列
    • 时间序列由两个基本因素构成： 1.研究对象所属时间 2.一定时间条件下数量特征的指标值
    • 时间序列统计指标值的表现形式： 1.绝对数时间序列 2.相对数时间序列 3.平均数时间序列
  • 二、时间序列的水平分析
    • 发展水平：时间序列中对应于具体时间的指标数值
    • 平均发展水平：时间序列中各时期发展水平计算的平均数（概括性描述现象在一段时期内所达到的水平）
    • 增长量与平均增长量： 1.增长量=报告期水平-基期水平 2.逐期增长量=报告期水平-报告期前一水平 3.累计增长量=报告期水平-最初水平 4.平均增长量=逐期增长量合计/逐期增长个数=累计增长量/（最末时间-最初时间）
  • 三、时间序列的速度分析
    • 发展速度：两个不同时期发展水平的比值（报告期水平/基期水平） 反应现象在一定时期内逐期发展变化的一般程度
    • 增长速度：两个不同时期增长水平的比值（报告增长量/基期水平） 反应现象在一定时期内逐期增长（降低）变化的一般程度
    • 就计算方法来说，重点是平均发展速度指标 平均增长速度=平均发展速度-1
  • 四、时间序列的分解和预测程序
    • 时间序列成分： 长期趋势（T）时间序列在较长一段时间内呈现的持续上升或下降的变动，趋势可能是线性或非线性的 季节变动（S）时间序列在一年内重复出现的周期性波动，如旅游、交通 循环波动（C）时间序列呈现出的非固定长度的周期性波动，如经济涨落的周期性波动 不规则波动（I）时间序列除去长期趋势、季节变动和循环波动之后的随机波动，一般指偶然引起的，难以预测和控制的
      • 一个时间序列可能只包含一种 也可能是由几种成分混合而成
    • 时间序列的预测（主要是根据历史数据）步骤： 第一步：确定时间序列所包含的成分 第二步：找出适合该时间序列的预测方法 第三步：对可能的预测方法进行评估，以确定最佳预测方案 第四步：利用最佳预测方案进行预测
  • 五、平滑预测法：目的是“消除”时间序列的不规则成分所引起的随机波动 ，适用于平稳时间序列的预测， 即没有明显的趋势、循环和季节波动的时间序列，如居民消费价格指数