Econometrics

Econometrics Chapter 1 The Nature of Econometrics and Economics Data Chapter 2 The Simple Regression Model Chapter 3 Multiple Regression Analysis :Estimation Chapter 4 Multiple Regression Analysis :Inference  Chapter 6 Multiple Regression Analysis :Further Issues Chapter 7 Multiple Regression Analysis with Qualitative Information  Chapter 8 Heteroskedasticity  Chapter 10 Basic Regression Analysis with Time Series Data Chapter 12 Serial Correlation and Heteroskedasticity in Time Seri

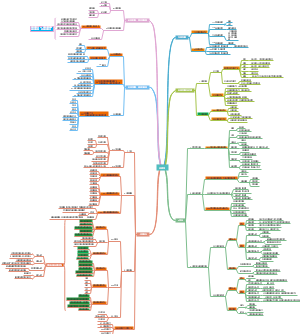
Econometrics

• Chapter 1 The Nature of Econometrics and Economics Data
  • Definition of Econometrics
    • use of statistical methods to analyze economic data
    • data form
      • experimental data 
      • nonexperimental data 
        • Econometrics typically analyze 
  • Typical goals of econometrics analysis
    • Estimating relationship between economic variables
    • Testing economic theories and hypotheses
    • Forecasting economic variables
    • Evaluating and implementing government and business policy
    • "ETFE "
  • Steps in econometric analysis
    • Economic model (this step is often skipped )
      • Maybe micro-or macromodels
      • Often use optimizing behavior,equilibrium modeling,...
      • Establish relationships between economic variables
      • Example :demand equation,pricing equation,...
      • 理论模型，是一种函数关系
        • Functional form of relationship not specified
        • Equation could have been postulated without economic modeling
    • Econometric model
      • 计量模型，是一种相关关系
        • The functional form has to be specified
        • Variable may have to be approximated by other quantities 
      • Most of econometrics deals with the specification of the error
      • May be used for hypothesis testing
  • Econometrics analysis 
    • Requires economic data
      • Cross-sectional data 随机抽样而来，离散性高
        • Sample of individuals,households,firms cities,states,countries,or other units of interest at a given point of time /in a given period
        • Cross-sectional observations are more or less independent
        • Sometimes pure random sampling is violated,e.g.units refuse to respond in surveys,or if sampling is characterized by clustering
        • Cross-sectional data typically encountered in applied microeconomics
        • For example,pure random sampling from a population
      • Time series data
        • Observations of a variable or several variables over time
        • Time series observations are typically serially correlated
        • Ordering of observations conveys important information
        • Data frequency:daily,weekly,monthly,quarterly.,annually,….
        • Typical features of time series:trends and seasonality
        • Typical applications:applied macroeconomics and finance
        • For example,stock prices,money supply,consumer price index, gross domestic product,annual homicide rates,automobile sales,..
      • Pooled cross data
        • Two or more cross sections are combined in one data set
        • Cross sections are drawn independently of each other
        • Pooled cross sections often used to evaluate policy changes
        • Example
          • Random sample of house prices for the year 1993
            • Evaluate effect of change in property taxes on house prices
          • A new random sample of house prices for the year 1995
          • Compare before/after (1993:before reform,1995:after reform)
      • Panel /Longitudinal data
        • The same cross-sectional units are followed over time
        • Panel data have a cross-sectional and a time series dimension
        • Panel data can be used to account for time-invariant unobservables
        • Panel data can be used to model lagged responses
        • Example
          • City crime statistics;each city is observed in two years
          • Time-invariant unobserved city characteristics may be modeled
          • Effect of police on crime rates may exhibit time lag
  • Causality and the notion of ceteris paribus
    • Definition of causal effect of x on y:
      • "How does variable y change if variable x is changed but all other relevant factors are held constant"
    • Most economic question are ceteris paribus question
    • It is important to define which causal effect one is interested in
    • It is useful to describe how an experiment would have to be designed to infer the causal effect in question
• Chapter 2 The Simple Regression Model
  • Definition
    • Explains of the simple linear regression model
    • 
      • y:explained variable
      • βο:intercept
      • β1:slope parameter
      • x:explained variable
      • u:error term
    • interpretation 
      • △y/△x=β1
      • △u/△x=0
  • Conditional mean independence assumption 
    • E(u|x)=0
      • The explanatory variable must not contain information about the mean of the unobserved factors
  • Population regression function (PFR)
    • x变动一个单位，y的条件期望变动β1个单位
      • y为正态分布——>u为正态分布
      • 大多数数据分布在均值附近，所以抽样数据更具有代表性
  • Ordinary Least Squares(OLS) estimates
    • • β1(hat)的大小与x，y间的相关性没有联系
    • • 线在点中间
      • E(u|x)=0
      • 回归线在点中间
    • Fitted values and residuals
    • Algebraic properties of OLS regression 
      • • Deviations from regression line sum up to zero
      • • Covariance between deviations and regressions is zero
      • • Sample averages of y and x lie on regression line
    • Goodness-of-fit 
      • Measures of Variation
        • • 离差(Total variation )
        • • 回归平方和(Explained part )
        • • 残差平方和(Unexplained part )
        • SST=SSE+SSR
      • Measure 
        • R-squared （拟合优度/判定系数/决定系数）
          • • R-squared越大，拟合地越好
          • R-squared 不是判定模型是否有用的依据
          • A high R-squared does not necessarily mean that the regression has a causal interpretation !
    • Expected values and variances of the OLS estimators 
      • • Unbiasedness of OLS 
      • • SST 越大，估计区间越小，估计就越准确，因此SST 不能等于0
        • Variances of the OLS estimators 
  • Standard assumptions for the linear regression model 
    • Assumption SLR.1
      • Linear in parameters 
        • 
          • In the population,the relationship between y and x is linear
    • Assumption SLR.2
      • Random sampling
        • 
          • The data is random sample drawn from the population
            • 简单随机抽样
            • 分层抽样
            • 系统抽样
            • 整群抽样
        • 
          • Each data point therefore follows the population equation
    • Assumption SLR.3
      • Sample variation in the explanatory variable
        • • The values of the explanatory variables are not all the same
    • Assumption SLR.4
      • Zero conditional mean
        • • The value of the explanatory variable must contain no information about the mean of the unobserved factors
    • Theorem2.1
    • Assumption SLR.5
      • Homoskedasticity
        • 
          • The value of the explanatory variable must contain no information about the variability of the unobserved factors
    • Theorem 2.2
  • Incorporating nonlinearities 
    • Logarithmic form
      • Log-logarithmic form
        • 当x增加量改变1％时，歪的增加量改变△log(y)/y％个单位
        • Logarithmic changes are always percentage changes 
        • The log-log form postulates a constant elasticity model
  • Estimating the error variance 
    • • 
    • standard errors 
• Chapter 3 Multiple Regression Analysis :Estimation
  • Definition
    • Explain variable y in terms of variables x 1,x 2,…x k
    • • β1:除了x1以外，其他变量都不变时x1对y的影响
      • β1等
        • simple:直接＋间接影响
        • multiple:直接影响
      • 当simple与multiple中的β1相等时，r(x1，xi)=0
      • 解释变量:k个，参数:k＋1个
      • β1…βk
        • simple:回归系数
        • multiple:偏回归系数(partial)
      • 不能凭借β间的大小来判断解释变量对被解释变量的影响程度
        • 因为解释变量间的数量级不同
    • • 当其他参数和误差项保持不变时，第j个解释变量xj变动一个单位，y变动βj个单位
  • Motivation for multiple regression 
    • Incorporate more explanatory factors into the model
    • Explicitly hold fixed other factors that otherwise would be in u
    • Allow for more flexible functional forms
  • Multivariate model 
    • 二元(three-variable model)
    • k元(k＋1-variable model)
  • OLS Estimation
    • Fitted values and residuals 
    • Algebraic properties of OLS regression 
    • Why does this procedure work ?
      • The residuals from the first regression is the part of the explanatory variable that is uncorrelated with the other explanatory variables
      • The slope coefficient of the second regression therefore represents the isolated effect of the explanatory variable on the dep. variable
    • Goodness-of-Fit 
      • R-squared 
    • Expected values and variances of the OLS estimators 
      • 
        • Unbiasedness of OLS
      • • 1/(1－R^2)叫做VIF （方差膨胀因子）
          • VIF 越大，共线性越严重
            • 0＜VIF ＜10,不存在多重共线性
            • VIF ≥10（R^2≥0.9）,存在多重共线性
          • VIFj ＝1/（1-Rj^2）
        • Rj^2:用其他变量解释xj时的R^2
        • Conclusion :x之间最好不相关
        • Sampling variances of the OLS slope estimators 
  • Standard assumptions for the multiple regression model 
    • Assumption MLR.1(经典线性模型假定)
      • Linear in parameters 
        • 
    • Assumption MLR.2
      • Random sampling
        • 
    • Assumption MLR.3
      • No perfect collinearity
        • In the sample (and therefore in the population), none of the independent variables is constant and there are no exact linear relationships among the independent variables
          • Imperfect correlation is allowed 
          • If an explanatory variable is a perfect linear combination of other explanatory variables it is superfluous（多余的） and may be eliminated（消除）
          • Constant variables are also ruled out（排除） (collinear with intercept)
        • 若存在共线，可增加样本量来调整
    • Assumption MLR.4
      • Zero conditional mean
        • 
          • In a multiple regression model, the zero conditional mean assumption is much more likely to hold because fewer things end up in the error
    • Theorem 3.1
    • Assumption MLR.5
      • Homoskedasticity
        • 
      • 不会有偏误
    • Theorem 3.2
      • Gauss-Makov Theory
        • BLUEs
          • 
          • 
        • Theorem 3.4
  • The variable problem of regression model
    • including irrelevant variables in a regression model 
    • omitting(漏掉) relevant variables 
      • 影响更大
      • All estimated coefficients will be biased
      • When is there no omitted variable bias
        • If the omitted variable is irrelevant or uncorrelated
  • Discussion of the multicollinearity problem 
    • lump (合并为一个)
      • because effects cannot be disentangled(分清) 
    • drop (删掉剩一个)
      • may reduce multicollineariy(but this may lead to omitted variable bias )
  • Estimating the error variance 
    • 
    • 
      • Theorem 3.3
        • Unbiased estimated of the error variance 
  • Variances in misspecified models 
    • 
      • It might be the case that the likely omitted variable bias in the misspecified model 2 is overcompensated by a smaller variance
    • 
      • Conditional on x1 and x2, the variance in model 2 is always smaller than that in model 1
        • 
          • Do no include irrelevant regressors
        • 
          • Trade off bias and variance.bias will not vanish even in large samples
  • Estimating of the sampling variance of the OLS estimators 
    • 
      • sd :观测值的方差
    • 
      • se:估计量的方差
• Chapter 4 Multiple Regression Analysis :Inference 
  • Statistical inference in the regression model
    • Hypothesis tests about population parameters
    • Construction of confidence intervals
  • Sampling distributions of the OLS estimators
    • We already know their expected values and their variances
    • However, for hypothesis tests we need to know their distribution
    • In order to derive their distribution we need additional assumptions
    • Assumption about distribution of errors: normal distribution
  • Assumption MLR.6 Normality of error terms
    • 
      • Theorem 4.1&4.2
        • 4.1 Normal sampling distributions 
        • 4.2 t-distribution for the standardized estimators
          • 
          • The t-distribution is close to the standard normal distribution if n-k-1 is large
    • 
      • independently of xi1,xi2,…,xik
  • testing
    • Hо:怀疑结果(大概率事件) H1:样本呈现结果(小概率事件)
      • t-test
        • 检验对单个总体参数的假设（检验变量的有效性，临界值为2）
          • testing hypotheses about a single population parameter
            • Hо:βj＝0
            • t-statistic(t-ratio )
            • Rejection region
              • one-sided
              • two- sided
                • • Confidence intervals
                    • • 左C0.05:Lower bound of the Confidence interval
                      • 右C0.05:Upper bound of the Confidence interval
                      • 0.95:Confidence level
            • Statistically significant
              • |t－ratio |＞1.645
                • statistically significant at 10% level
              • |t－ratio |＞1.96
                • statistically significant at 5% level
              • |t－ratio |＞2.576
                • statistically significant at 1% level
          • testing more general hypotheses 
            • Hо:βj＝aj
            • t-statistic
              • 
        • 用t检验删无关变量前提
          • 数据充分，可靠
        • Testing hypotheses about a linear combination of the parameters 
          • 
          • 
          • Define θ1＝β1-β2 and test Hо:θ1＝0 against H1:θ1＜0
      • F-test
        • 对多个线性约束的检验（检验模型的有效性，临界值为4）
          • Testing multiple linear restrictions
            • 
              • q:number of restrictions
            • Example 
              • Hо:β3＝0，β4＝0，β5＝0 against H1:Hо is not true
                • 若Hо成立，责二元和五元无差别
                  • The likely reason is multicollinearity between them 
            • Rejection region 
              • 
          • Testing of overall significance
            • 
            • The test of overall significance is reported in most regression packages; the null hypothesis is usually overwhelmingly rejected
        • The F-testworks for general multiple linear hypotheses
  • For all tests and confidence intervals, validity of assumptions MLR.1 – MLR.6 has been assumed
• Chapter 6 Multiple Regression Analysis :Further Issues
  • More on using logarithmic functional forms 
    • positive 
      • Convenient percentage/elasticity interpretation 
      • Slope coefficients of logged variables are invariant to rescalings (缩小尺度)
      • Taking logs often eliminates /mitigates problems with outliers (异常值)
      • Taking logs often helps to secure normality and homoskedasticity 
    • drawback 
      • Variables measured in units such as years should not be logged 
      • Variables measured in percentage points should also not be logged 
      • Logs must not be used if variables take on zero or negative values
      • It is hard to reverse(还原) the log-operation when constructing predictions
  • More on Functional Form 
    • Logarithmic functional forms 
    • Quadratic functional forms 
    • Models with interaction terms
      • 
        • β2:Effect of x2,but for x1 of zero
          • so interaction effects complicate interpretation of parameters
      • Reparametrization of interaction effects
        • • δ2:effect of x2 if all variables take on their mean values
          • μ1.μ2:population means ;may be replaced by sample means
        • advantages 
          • Easy interaction of all parameters
          • Standard errors for partial effects at the mean values available 
          • If nnecessary interaction may be centered at other interesting values
  • General remarks on R-squared 
    • A high R-squared does not imply that there is a causal interpretation
    • A low R-squared does not preclude precise estimation of partial effects
  • Adjusted R-squared 
    • 
      • punishment :k越大，R^2越小
    • Adjusted R-squared 比较条件
      • 相同变量
      • 多元模型
    • 
      • 当adjusted R-squared <0时，将其看做等于零，即拟合程度差
  • Nonnested model 
    • 
      • In the given example,even after adjusting for the difference in degree of freedom,the quadratic model is preferred
  • Adding regressors to reduce the error variance
    • may excarcerbate(排除) multicillinearity problem
    • reduce the error variance
    • Variables that are uncorrelated with other regressors should be added because they reduce error variance without increasing multicollinearity
    • However,such uncorrelated variables may be hard to find 
• Chapter 7 Multiple Regression Analysis with Qualitative Information 
  • Qualitative Information 
    • A way to incorporate qualitative information is to use dummy variables
    • They may appear as the dependent or as independent variables
  • A single dummy independent variable 
    • example
      • • δо=0:基准(bench mark)男性
        • δ0＜0:其他不变时，wage女性＜男性
          • 当female=1时，截距为βо+δо
          • 当female=0时，截距为βо
    • Using dummy explanatory variables in equations for log(y)
      • 
      • 
        • 当x4变动一个单位时，y改变a%
  • Dummy variances 
    • Dummy variable trap
      • single category
        • 某一定性变量有k个分类时，应选k-1个哑变量
      • multiple categories
    • 用途
      • 政策评价
      • 政策评估
      • 模型比较
  • Interaction involving dummy variables 
    • 改变Slope(有交互项) 还是Intercept (有哑变量) ?
      • 都引入方程进行t检验判断
        • example
          • 
          • 
          • Hypotheses
            • Hо:δ1=0
              • The return to education is the same for men and women
            • Hо:δо=0，δ1=0
              • The whole wage equation is the same for men and women
          • 
          • Conclusion 
            • No evidence against hypothesis that the return to education is the same for men and women
            • the effect for educ = 0
    • 模型比较
      • F检验
  • The linear probability model
    • Disadvantages 
      • Predictedprobabilities may be larger than one or smaller than zero
      • Marginal probability effects sometimes logically impossible.
      • The linear probability model is necessarily heteroskedastic
      • Heteroskedasticity consistent standard errors need to be computed
    • Advantages 
      • Easy estimation and interpretation
      • Estimated effects and predictions are often reasonably good in practice
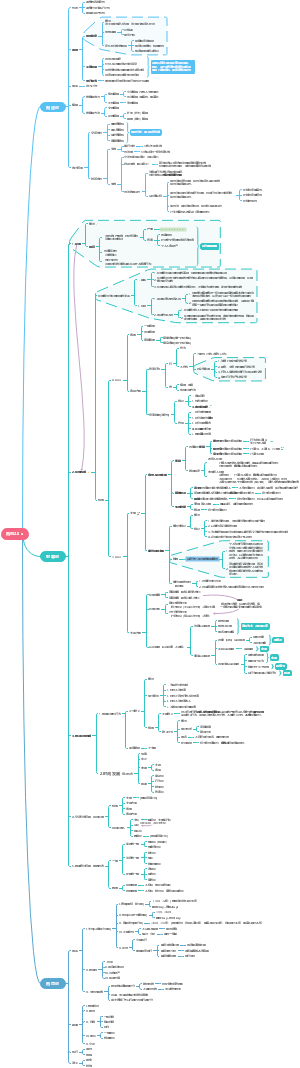
• Chapter 8 Heteroskedasticity 
  • 
  • 指回归规模型中扰动项的方差不全相等，即随机扰动项不再是一个常数
  • Consequences of heteroskedasticity for OLS 
    • OLS still unbiased and consistent under heteroskedasticity (有效性？?)
    • interpretation of R-squared is not changed 
      • 
    • invalidates variance formulas for OLS estimators 
    • The usual F tests and t tests are not valid
    • OLS is no longer the best linear unbiased estimator (BLUE )there may be more efficient linear estimators
  • Heteroskedasticity-robust inference after OLS estimation
    • Formulas for OLS standard errors and related statistics have been developed that are robust to heteroskedasticity of unknown form
    • All formulas are only valid in large samples
    • Formula for heteroskedasticity-robust OLS standard error
      • 
      • robust se may be larger or smaller,the difference are often small in practice
    • Using these formulas, the usual t test is valid asymptotically
    • The usual F statistic does not work under heteroskedasticity, but heteroskedasticity robust versions are available in most software
  • Testing for heteroskedasticity 
    • Breusch-Pagan test (BP test)
      • Hypotheses 
        • 
        • • 方程有效，则存在异方差
      • F检验
        • 
      • LM检验(拉格朗日乘数检验或卡方检验)
        • 
        • 
      • 在某种程度上，取对数可以消除异方差
        • 不严重的才可以
        • 改变了方程的经济含义
    • White test
      • Hypotheses 
        • 
        • 
      • more general
      • disadvantage 
        • Including all squares and interactions leads to a large number of estimated parameters (e.g. k=6 leads to 27 parameters to be estimated)
  • Weighted least squares (MLS )estimation
    • 目的
      • 将方差修均匀
    • 权重h(xi)的确定
      • 大方差小权重，小方差大权重
        • h已知
        • h未知
          • 估计
    • 
    • 
    • Why is WLS more efficient than OLS in the original model?
      • Observations with a large variance are less informative than observations with small variance and therefore should get less weight
    • 
    • If the observations are reported as averages(平均数) at the city/county/state/-country/firm level, they should be weighted by the size of the unit
  • model selection (不知道是否存在异方差时)
    • step 1
      • 比较方差，选出差异较大者
    • step 2
      • 比较R^2，选择最大者
  • WLS in the linear probability model
    • 
    • Discussion 
      • Infeasible if LPM predictions are below zero or greater than one
      • If such cases are rare, they may be adjusted to values such as 0.01/.099
      • Otherwise, it is probably better to use OLS with robust standard errors
• Chapter 10 Basic Regression Analysis with Time Series Data
  • The nature of time series data
    • may not be arbitrarily reordered
    • typical feature :serial correlation ,tendency,seasonality
  • Regression models 
    • static models
      • 
    • finite distributed lag models
      • 
        • 
          • effect of a transitory shock
        • 
          • effect of a permanent shock
        • 
      • Assumption 
        • Assumption TS.1
          • Linear in parameters 
            • 
        • Assumption TS.2
          • No perfect collinearity
        • Assumption TS.3
          • Zero conditional mean
            • 
        • Theorem 10.1
          • 
        • Assumption TS.4
          • Homoskedasticity
            • 
              • easily violated
        • Assumption TS.5
          • No serial correlation
            • 
        • Theorem 10.2&10.3&10.4
          • 10.2
          • 10.3
            • 
          • 10.4
            • Gauss-Markov Theorem
        • Assumption TS.6
          • Normality 
            • 
        • Theorem 10.5
          • Normal sampling distributions The usual F-and t-tests are valid
• Chapter 12 Serial Correlation and Heteroskedasticity in Time Series Regressions
  • Properties of OLS with serially correlated errors 
    • OLS still unbiased and consistent if errors are serially correlated
    • Correctness of R-squared also does not depend on serial correlation
    • OLS standard errors and tests will be invalid if there is serial correlation
    • OLS will not be efficient anymore if there is serial correlation
  • Serial Correlation and Heteroskedasticity in Time Series Regression 
    • Serial correlation
      • Testing
        • DW test /AR(1)
          • 局限
            • 模型不能出现被解释变量的滞后项
            • 有两个不能确定的区间
            • 只能是线性一阶自相关
        • BG(LM) test /AR(q)
      • Correcting
        • Generalized difference
          • 
            • 判断y*和x*是否有自相关即可
          • 
        • Cochrane-Orcutt estimation
        • Prais-Winsten estimation
    • Heteroskedasticity
• Chapter 13 Polling Cross Sections across Time :Simple Panel Data Method 
  • Policy analysis 
  • difference-in-difference (DiD)estimator 
• Chapter 14 Advanced Panel Data Method 
• 浮动主题
• 简洁方便 只能判断线性一阶自相关,并且n必须足够大