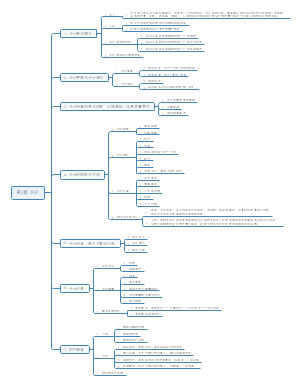
期权价值评估

期权价值评估 注会 注册会计师 CPA 财务管理，期权是一种合约，赋予持有人在某一特定日期或该日期之前的任何时间，以固定价格购入或售出约定数量某种资产的权力。

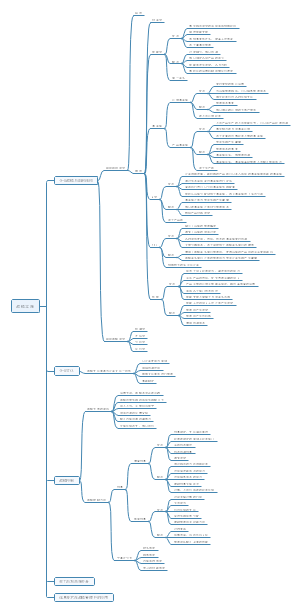
期权价值评估

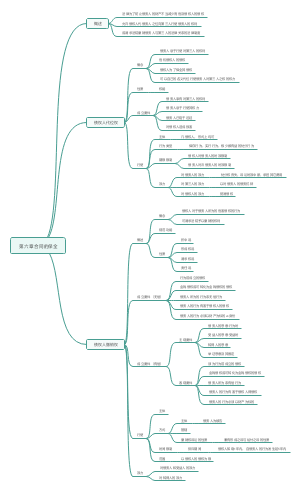
• 期权的概念、类型、投资策略
  • 期权的概念
    • 一种合约，赋予持有人在某一特定日期或该日期之前的任何时间，以固定价格购入或售出约定数量某种资产的权力
      • ①赋予持有人一种权力：只享受权利，不承担义务
        • 买方（持有人）：有权选择行权或放弃
        • 卖方（出售方）：只能被动配合
      • ②期权的标的资产：合同中约定的买入或卖出的资产（本章只讨论股票期权）
        • 期权买卖双方，一方不一定真的有股票，可以“卖空”，另一方也不一定真的项目股票
        • 买方行权不一定要进行股票交割，直接补差价就好
      • ③期权的执行及执行价格
        • 执行：期权持有人按合约约定，购入或售出标的资产的行为，又称为“行权”
        • 执行价格：合约约定的、购入或售出标的资产的固定价格
      • ④期权的到期日
        • 合约约定的到期日，在这一天之后，期权失效
          • 按行权时间分类
            • 欧式期权：持有人只能在期权到期日选择行权或放弃
            • 美式期权：持有人可以在期权到期日或之前的任何时间行权
      • ⑤期权的到期日价值：期权到期日的净收入，取决于标的资产的到期日市价和执行价格
        • 期权买方：有特权，到期日价值≥0，不可能为负
        • 期权卖方：只能被动配合买方，到期日价值≤0
        • 买方的到期日价值+卖方的到期日价值=0（双方交易，零和博弈） 买方的到期日价值=-卖方的到期日价值 计算技巧，先计算买方的到期日价值，再计算卖方的到期日价值，有了买方到期日价值后，前面加个-号即为卖方的到期日价值
      • ⑥期权成本及期权净损益
        • 期权买方：支付成本获得期权 期权买方净损益=期权买方到期日价值-期权成本
        • 期权卖方：出售期权收到售价 期权卖方净损益=期权卖方到期日价值+期权售价
  • 期权的类型
    • 期权按合约赋予期权持有人（买方）的权力分类
      • 看涨期权（call）：赋予持有人以固定价格购买标的股票的权力，即“买权”、“择购期权”
      • 看跌期权（put）：赋予持有人以固定价格出售标的股票的权利，即“卖权”、“择售期权”
    • 期权交易至少有买卖双方
      • 看涨期权
        • 买方：享有按执行价格买股票的特权
        • 卖方：承担配合卖方的义务
      • 看跌期权
        • 买方：享有按执行价格卖股票的特权
        • 卖方：承担配合卖方的义务
    • 看涨期权
      • 买入看涨期权（多头看涨）：买方付出成本获得看涨期权，期权到期日有权选择购买标的股票或放弃
        • 到期日股价>执行价格，买方会行权，到期日价值（净收入）>0
        • 到期日股价<执行价格，买方不会行权，到期日价值（净收入）=0
        • 到期日股价=执行价格，买方不会行权，到期日价值（净收入）=0
        • 1、买入看涨期权的净损失有限，买方最多损失期权成本 2、买入看涨期权的净收益无限，股价越高，买方净收益越大
      • 卖出看涨期权（空头看涨）：卖方收取期权售价、出售看涨期权，期权到期日如果买方选择行权（购买标的股票），卖方则需要被动配合
        • 到期日股价>执行价格，买方会行权，买方到期日价值（净收入）>0，卖方到期日价值=-买方到期日价值<0
        • 到期日股价<执行价格，买方不会行权，到期日价值（净收入）=0,卖方到期日价值=0
        • 到期日股价=执行价格，买方不会行权，到期日价值（净收入）=0，卖方到期日价值=0
        • 1、卖出看涨期权的净收益有限，卖方最高收益为期权售价 2、卖出看涨期权的净损失无限，股价越高，卖方损失越大
    • 看跌期权
      • 买入看跌期权（多头看跌）：买方付出成本、获得看跌期权，期权到期日有权选择出售标的股票或放弃
        • 到期日股价<执行价格，买方会行权，到期日价值>0
        • 到期日股价=执行价格，买方不会行权，到期日价值=0
        • 到期日股价>执行价格，买方不会行权，到期日价值=0
        • 1，买入看跌期权净损失有限，买方最多损失期权成本 2，买入看跌期权，股价越低，买方净收益越大，净收益最大值=期权执行价格-期权成本
      • 卖出看跌期权（空头看跌）：卖方收取期权售价，出售看跌期权，期权到期日如果卖方选择行权（购买标的股票），卖方则需要被动配合
        • 到期日股价<执行价格，买方会行权，买方到期日价值>0，卖方到期日价值=-买方到期日价值<0
        • 到期日股价<执行价格，买方不会行权，到期日价值（净收入）=0,卖方到期日价值=0
        • 到期日股价=执行价格，买方不会行权，到期日价值（净收入）=0，卖方到期日价值=0
        • 1，卖出看跌期权净收益有限，卖方净收益最大值为期权成本 2，卖出看跌期权，股价越低，卖方净损失越大，净损失最大值=期权执行价格-期权成本
  • 期权的投资策略：构造不同投资组合，可以充分发挥股票期权的作用，控制投资风险
    • 买入股票，同时配合一种期权
      • 保护性看跌期权：买股票同时买入该股票的看跌期权，买入1股股票，同时买入该股票的一股看跌期权
        • 股价上涨：股票获利，但看跌期权不行权，损失期权成本
        • 股价下跌：股票受损，但看跌期权可能会行权，可以贴补股票损失
        • 组合降低了投资净损益的预期值
      • 抛补性看涨期权：买股票同时卖出该股票的看涨期权，买入1股股票，同时卖出该股票的1股看涨期权
        • 股价上涨：卖出的看涨期权可能被行权，但股票获利
        • 股价下跌：股票亏损，但卖出的看涨期权可能不被行权，赚取的期权售价可以贴补股票的损失
        • 组合降低了投资净损益的预期值
    • 不买股票只投资期权
      • 多头对敲：买入同一股票的看涨期权和看跌期权，要求两个期权的执行价格、到期日相同
        • 适用情景：预计股价将发生强烈变动，但不知道是大涨还是大跌
        • 股价上涨：看涨期权行权时，看跌期权肯定不行权
        • 股价下跌：看跌期权行权时，看涨期权肯定不行权
        • 1，最坏结果：到期日股价=执行价格，两个期权都不行权，白白损失两个期权的购买成本 2，好结果：到期日股价≠执行价格，总有一个期权可以行权，组合净收入>0，但如果到期日股价偏离执行价格变动不大，组合净损益可能小于0
      • 空头对敲：卖出同一股票的看涨期权和看跌期权，要求两个期权的执行价格、到期日相同
        • 适用情景：预计股价相对比较平稳
        • 股价上涨：看涨期权被执行时，看跌期权肯定不被行权
        • 股价下跌：看跌期权被行权时，看涨期权肯定不被行权
        • 1，最好结果：到期日股价=执行价格，两个期权都不被行权，白白赚取两个期权的出售价格 2，坏结果：到期日股价≠执行价格，总有一个期权要被行权，到期日净收入<0
  • 买卖权平价定理
    • 原理：构造一个投资组合，购入以1股股票为标的的看涨期权，同时购入一张到期日价值为该看涨期权执行价格的债权，让该组合和保护性看跌期权在到期日的净收入相同，则在市场均衡时，该组合的投资成本=保护性看跌期权的投资成本
    • 例： ①买入1股A公司股票的欧式看涨期权，执行价格100元，期限1年；同时购入一张1年后到期、到期日价值（本利和）为100元的债券（假设投资该债券无风险） ②买入1股A公司股票，购入价格100元，同事购入1股该股票的欧式看跌期权，执行价格100元，1年后到期 对比两种投资方式在1年后的收入相同
    • 推理公式：C0+PV（X)0=C+X/(1+r)=S0+P0 C:以某股票为标的的看涨期权的价值 X：期权的执行价格 PV（X）：期权执行价格现值 r：期权有效期对应的无风险利率 S：该股票的现行市价 P：以同一股票为标的的看跌期权的价值
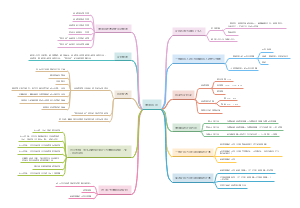
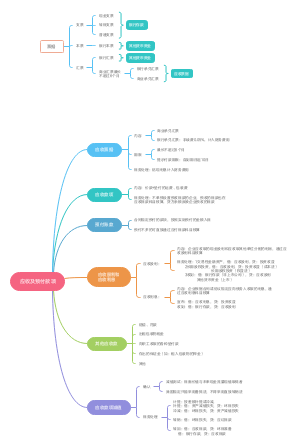
• 金融期权价值评估
  • 金融期权价值的影响因素
    • 金融期权价值的构成内容（从期权持有人（买方）角度出发：期权价值=期权内在价值+期权时间溢价
      • 期权内在价值：期权买方立即执行期权产生的经济价值，取决于标的股票的现行市价和执行价格的高低
        • ·到期日，期权内在价值=期权到期日价值
        • ·到期日之前，期权的内在价值不一定等于期权到期日价值
        • ·期权有效期内，期权内在价值是变化的，期权有效期内任意一天，对于期权持有人而言：
          • ①对持有人有利时，期权处于实值状态
            • 看涨期权：现行股价>执行价格
            • 看跌期权：现行股价<执行价格
          • ②对持有人不利时，期权处于虚值状态
            • 看涨期权：现行股价<执行价格
            • 看跌期权：现行股价>执行价格
          • ③现行股价=执行价格，期权处于平价状态
      • 期权的时间溢价：是等待的价值，时间带来的标的资产价值的波动，定性推理，寄希望于随着时间的推移，股价会发生变化，从而增加期权到期日行权的可能性
        • ·距离到期日越远，期权时间溢价越大
        • ·到期日，期权价值=期权内在价值=期权到期日价值，期权的时间溢价=0
    • 影响因素包括
      • 讨论某因素的影响，以假定其他因素不变为前提
      • 股票市价
        • 看涨期权：股价越高，期权价值越高
        • 看跌期权：股价越高，期权价值越低
      • 执行价格
        • 看涨期权：执行价格越高，期权价值越低
        • 看跌期权：执行价格越高，期权价值越高
      • 到期期限
        • 欧式期权：不确定
        • 美式期权：期限越长，期权价值越高
      • 预期红利：股票发放红利，股价下降，但期权持有人不享受分红
        • 看涨期权：预期发放红利，股价下降，期权价值下降；
        • 看跌期权：预期发放红利，股价下降，期权价值上升
      • 无风险利率：影响期权执行价格的现值，结合买卖权平价[C+X/（1+r)=S+P]
        • 看涨期权：无风险利率r越大，执行价格的现值越小，期权价值越高
        • 看跌期权：无风险利率r越大，执行价格的现值越小，期权价值越低
      • 股价波动率：最重要的因素，股价波动率越大，期权价值越高
  • 金融期权价值的评估方法：布莱克-斯科尔斯期权定价模型（B-S模型）
    • 金融期权价值评估原理
      • 套期保值原理（复制原理）：构造一个“股票和借款”的投资组合，让该组合到期日净收入等于以1股该股票为标的的看涨期权的到期日净收入
        • ①构建投资组合：以期权有效期对应的无风险利率r借入款项B，以现行股价S0购入股票H（套期保值比率δ）股，该组合的投资成本=H*S0-B
        • ②预计期权到期日股价上涨幅度，下跌幅度，计算股价上行成熟u，股价下行乘数d
          • 假设股价上涨下跌幅度可以准确预测
          • u=1+股价上涨幅度
          • d=1-股价下跌幅度
        • ③计算到期日股价Su，Sd
          • Su=S0*u
          • Sd=S0*d
        • ④根据到期日股价，计算看涨期权到期日价值Cu,Cd
        • ⑤联立方程组，求H，B
          • 方程左边H*S0-B
            • 股价上涨：H*Su-B*（1+r）
            • 股价下跌：H*Sd-B*（1+r)
          • 方程右边C0
            • 股价上涨Cu
            • 股价下跌Cd
          • 联立解方程组： 股价上涨：H*Su-B*（1+r）=Cu 股价下跌：H*Sd-B*（1+r)=Cd 股价上涨-股价下跌：H=（Cu-Cd）/（Su-Sd）=（Cu-Cd）/S0*(u-d) B=(H*Sd-Cd)/(1+r）
        • ⑥市场均衡时：看涨期权初始价值=投资组合的初始投资成本，既：C0=H*S0-B
      • 风险中性原理：假设每个投资者对待风险的态度都是中性的，所有投资的报酬都等于无风险利率，包括投资股票或投资看涨期权，可以利用看涨期权到期日价值（净收入）、无风险利率，反推看涨期权的投资成本，即：看涨期权价值
        • ①预计看涨期权到期日股价上涨幅度、下跌幅度，计算股价上行时的报酬率、股价下行时的报酬率
          • 股价上行时的报酬率=股价上涨幅度
          • 股价下行时的报酬率=-股价下跌的幅度
        • ②计算股价上行概率、下行概率
          • 股价上行概率+股价下行概率=1
          • 股票投资的期望报酬率=股价上行概率*股价上行时的报酬率+股价下行概率*股价下行时的报酬率=看涨期权有效期对应的无风险利率
        • ③根据看涨期权到期日股价上涨幅度、下跌幅度，计算股价上行乘数u，股价下行乘数d，以及到期日股价Su、Sd，看涨期权到期日价值Cu、Cd
          • u=1+股价上涨幅度，Su=S0*u
          • d=1-股价下跌幅度，Sd=S0*d
        • ④结合股价上行概率、下行概率，计算看涨期权到期日价值的加权平均值： 看涨期权到期日价值=股价上行概率*Cu+股价下行概率*Cd=股价上行概率*Cu+（1-股价上行概率）*Cd
        • ⑤计算看涨期权的初始投资成本，即看涨期权初始价值
          • 看涨期权到期日价值=看涨期权初始价值*（1+看涨期权投资的期望报酬率）
          • 看涨期权初始价值=看涨期权到期日价值/（1+看涨期权投资的期望报酬率） =看涨期权到期日价值/（1+期权有效期对应的无风险利率）
    • 金融期权定价模型
      • 二叉树期权定价模型
        • 前提假设：
          • 市场投资无交易成本
          • 投资者都是价格的接受者
          • 可以卖空
          • 可以用无风险利率借入或贷出资金
          • 未来的股价要么按预期上涨、要么按预期下跌
        • 单期二叉树期权定价模型：以抛补性看涨期权投资组合为原型，当购入的股票达到一定数量时，投资组合能实现完全的套期保值，即：投资的期望报酬率=期权有效期对应的无风险利率
          • ①投资组合的初始投资成本=HS0-C0，投资组合的到期日价值=（HS0-C0）*（1+r）
          • ②完全的套期保值下：HSu-Cu=HSd-Cd=(HS0-C0)*(1+r),推导得出：C0=HS0-(HSu-Cu)/(1+r)
          • ③套期保值原理下，套期保值比率H=（Cu-Cd）/(Su-Sd)=(Cu-Cd)/S0*(u-d)
          • ④C0=HS0-(HSu-Cu)/(1+r)=(1+r-d)/(u-d)*Cu/(1+r）+（u-1-r)/(u-d)*Cd/(1+r)=p*Cu/(1+r)+(1-p)*Cd/(1+r)
        • 两期二叉树期权定价模型：将到期时间平分为两段，从而假定股价在期权有效期内变动两次，重复使用二叉树期权定价模型
        • 多期二叉树期权定价模型：期权有效期内时间无限次平分，股价变动周期无限缩短，最终股价连续变动
      • 布莱克-斯科尔斯期权定价模型
        • 前提假设：
          • 期权有效期内，标的股票不发股利，不做其他分配
          • 买卖股票或期权都没有交易成本
          • 短期无风险利率不变
          • 可以以短期无风险利率借入任何数量资金
          • 允许卖空
          • 欧式期权
          • 所有交易连续发生，股价随机游走