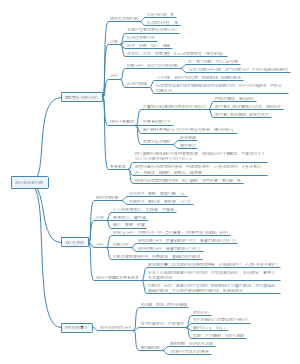
卫生学--分类变量资料的统计分析

卫生学，关于分类变量资料的统计分析，包括公式和相应解答

数值变量的统计资料分析

• 数值变量资料的统计描述
  • 集中趋势的描述
    • 平均数
      • 描述一组变量的集中趋势或平均水平的统计指标
      • 算数均数
        • 反应一组呈对称分布的变量值在数值上的平均水平
        • 总体均数用μ表示，样本均数用
        • 适用于对称分布或近似对称分布的资料
        • 计算方法
          • 直接法
            • 
          • 加权法
      • 几何均数
        • 反应一组经对数转换后呈对称分布或数据之间呈倍数关系或近似倍数关系资料的平均水平
        • 用字母G表示
        • 注意事项
          • 变量值中不能有0
          • 不能同时有正值和负值
        • 计算方法
          • 直接法
            • 
          • 加权法
      • 中位数
        • 适用于描述各种分布，尤其是非对称分布以及频数分布的一段或两端无确切数值的资料的平均水平
        • 用字母M表示
        • 偏态分布一般用中位数来描述集中趋势
        • 计算方法
          • 直接法
            • 当n为奇数时
              • 
            • 当n为偶数时
              • 
          • 频数表法
            • 
            • 式中，L、i、fx分别为Px所在组段的下限、组距和频数；∑fL为小于L的各组段的累计频数，n为总例数
    • 百分位数
      • 是一种位置指标
      • 用字母Px表示
      • 观察值从小到大排列，分成一百份，第x百分位次对应的数值称为第x百分位数，用Px表示
  • 离散趋势的描述
    • 描述数据变异程度的统计指标
    • 全距（极差）
      • 一组同质观察值中最大值与最小值之差
      • 用字母R表示
      • 全距越大，离散程度越大
      • 弊端
        • 1. 易受极端值的影响
        • 2. 且受样本含量n的影响较大，稳定性差
    • 四分位数间距
      • 上四分位数与下四分位数之差，即P75-P25
      • 用字母Q表示
      • 四分位数间距越大，离散程度越大
      • 适用于与中位数一起描述非正态分布资料的分布特征
    • 方差
      • 描述所有观察值与均数的平均离散程度的指标
      • 方差越大，离散程度越大
      • 计算公式
        • 总体方差
          • 
        • 样本方差
          • 
          • （n-1）为自由度
    • 标准差
      • 方差的算术平方根
      • 总体标准差用σ表示，样本标准差用s表示
      • 用途
        • 1. 反应一组计量资料的离散程度，标准差越大，变量值分布越分散
        • 2. 用于计算变异系数
        • 3. 用于计算标准误
        • 4. 结合均数与正态分布规律，估计参考值范围
      • 计算公式
    • 变异系数
      • 标准差与算数均数之比
      • 是一个度量相对变异程度的指标，以百分数的形式表示
      • 适用于观察指标的单位不同或均差相差较大时两组资料变异程度的比较
      • 计算公式
• 正态分布及其应用
  • 概念
    • 是一种连续型随机变量最常见的分布
    • 对于任何一个服从均数位μ、标准差为σ的正态分布变量，都可以通过变量的标准化变换
  • 特征
    • 1. 正态曲线在横轴上方，呈钟形，两端与横轴永不相交
    • 2. 正态分布以均数为中心，均数所在处最高，左右对称，正态曲线在X=μ±σ处有拐点
    • 3. 正态分布有两个参数，即均数与标准差（μ与σ）
      • 均数为位置参数，σ恒定，改变μ的值，曲线沿横轴平行移动，形状不变
      • 标准差为形状参数，μ恒定，σ越大，曲线越平坦，反之曲线越陡峭
    • 4. 正态分布曲线下的面积分布有一定的规律性
  • 应用
    • 制定参考值范围
      • 1. 从正常人的总体中进行随机抽样
      • 2. 对选定的正常人进行准确的测定
      • 3. 确定取单侧范围还是双侧范围
      • 4. 选择适当的白百分范围
      • 5. 根据资料的分布类型选用恰当的估计方法
      • 以制定95%的参考值范围为例
• 数值变量资料的统计推断
  • 均数的抽样误差与标准误
    • 概念
      • 抽样误差
        • 由抽样引起的样本均数与总体均数之间的差异或样本均数之间的差
      • 标准误
        • 样本均数的标准差
        • 是描述均数的抽样误差大小的统计指标
        • 标准误越大，抽样误差越大
        • 计算公式
          • 理论值
          • 估计值
        • 用途
          • 1. 可用来衡量样本均数的可靠性
          • 2. 与样本均数结合，可用于估计总体均数的置信区间
          • 3. 可用于进行均数的假设检验
    • 中心极限定理
      • 1. 从均数为μ标准差为σ的正态总体中随机抽取例数为n的样本，样本均数服从均数为μ，标准差为σxba的正态分布
      • 2. 当样本含量n足够大时，即使是从非正态分布总体抽样，样本均数xba分布也会逼近正态分布
  • t分布
    • 概念
    • 计算公式
      • v为自由度，v=n-1
    • 几个知识点
      • t分布是一簇对称于0的单峰分布曲线
      • 自由度越大，曲线越扁平，随着自由度的增大，随着自由度的增大，t分布曲线逐渐逼近标准正态曲线
      • t界值表中可以看出 在同一自由度下，t值越大则P值越小 P值相同时，自由度越大则t值越小，同时接近z值 当自由度为无穷大时，t值与z值相等
  • 总体均数置信区间估计
    • 概念
      • 总体参数有多一定的可能性落在我们规定的区间里
      • 用CI来代替
      • 置信度用1-ɑ表示
    • 方法
      • 区间估计
        • σ已知时，按正态分布原理
        • σ为止、样本例数较小时，一般按t分布原理
        • σ未知，但样本例数n足够大（n≧100）时，按正态分布原理
        • 置信度为95%
    • 注意区别
    • 注意
      • 可信区间时随机的，总体参数时固定的
      • 可信区间包括两个要素
        • 准确度
          • 反应在可信区间的大小上，区间包含总体均数的概率大小，越接近1越好
        • 精度
          • 反应在区间的长度，越小越好
  • 假设检验的基本思想和步骤
    • 两种假设
      • 零假设
        • H0
        • μ=μ0
        • 差异是由抽样误差所造成的
      • 备择假设
        • H1
        • μ≠μ0
        • 差异是由于样本总体不同
    • 基本步骤
      • 建立假设，确定检验水准ɑ
      • 选定检验方法和计算检验统计量
      • 确定P值和作出推断结论
• 方差分析
  • 应用条件： ①各样本是相互独立的随机样本 ②各样本都来自正态分布 ③个样本的总体方差相等 基本思想： 总变异=组间变异（研究因素和随机误差导致）+组内变异（随机误差导致） F=组间变异/组内变异
  • 完全随机设计资料的方差分析
    • 计算公式
  • 随机区组设计资料的方差分析
    • 计算公式
  • 多个样本均数间两两比较的q检验
    • 计算公式
      • MS误差为单因素方差分析中的组内均方MS组内
    • v为组内均方的自由度
    • a为组数
• 假设检验应注意的问题
  • 假设检验中的两类错误
    • Ⅰ型错误
    • Ⅱ类错误
    • 不会
  • 假设检验中的注意事项
    • 1. 资料必须合乎随机化抽样和随机化分组原则
    • 2. 选用的假设检验方法应符合其实用条件
    • 3. 实际差别大小与统计意义的区别
    • 4. 假设检验时对差异有无统计学意义的判断不能绝对化
    • 5. 假设检验的单侧检验与双侧检验的选择
• t检验和z检验
  • t检验用于当样本例数n较小，样本来自正态分布总体，总体标准差未知，在作两样本均数比较时，还要求两样本相应的两总体方差相等 z检验则主要适用于两样本含量较大（均大于50）的情况
  • 单样本资料的t检验
    • 目的
      • 推断样本所来自的未知总体均数μ与已知的总体均数μ0是否有差别
  • 配对设计资料的t检验
    • 适用情况
      • 1. 自身比较，是指同一受试对象处理前后的比较
        • 目的是推断这种处理有无作用
      • 2. 同一受试对象的两个部位测同一个指标所得的结果
      • 3. 同一样品用两种方法测同一指标所得的结果
      • 4. 对每个对子中的两个受试对象分别给予两种处理
      • 目的都是推断两种处理的效果有无差别
    • 计算公式
      • d杠为差值的样本均数，sd杠为差值均数的标准误，速度、为差值的标准误，n为对子数
  • 两独立样本资料的t检验和z检验
    • 两独立样本资料的t检验
      • 两样本含量较小，且均来自正态分布、总体方差相等是可用
      • 计算公式
    • 两独立样本的z检验
      • 两个样本含量较大（均＞50）时用