第十一章空间与向量几何

高等数学第十一章空间与向量几何，知识内容有向量、点积、三维笛卡尔坐标、向量值函数与曲线运动、三维空间中的直线和切线等。

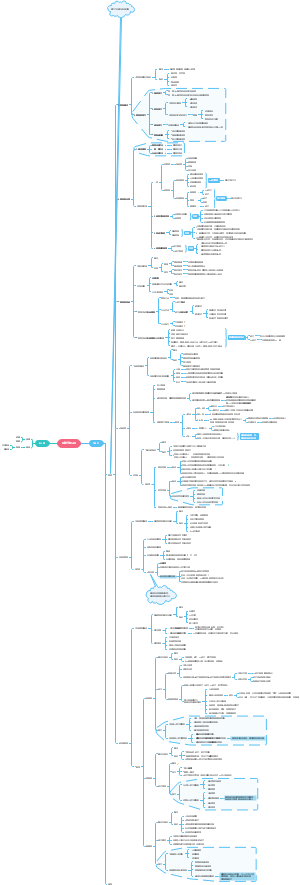
Chapter 11 Geometry in Space and Vectors

• 11.5 Vector-Valued Functions and Curvilinear Motion
  • Vector-Valued Function
  • Theorem A
  • Theorem B Differentiation Formulas
  • Physical applications
    • Velocity
    • Acceleration
    • Speed
  • Exercises
    • Find the derivative of the Vector-Valued Functions
    • Find the velocity, acceleration and speed at a specific t
• 11.6 Lines and Tangent Lines in Three-Space
  • The direction vector of the line
  • The equation of the line
  • Parametric equation
    • x=x0+at y=y0+bt z=z0+ct
  • Symmetric equation
  • Tangent Line to a curve
    • The tangent line to the curve has direction vector
  • Exercises
    • Find the equation of the line through two points
      • 1 Find the direction vector
      • 2 Write down the equation
    • Find the equation of the line of intersection of two planes
      • Solution 1
        • 1 Find two points on the line of intersection (set x=0 and y=0)
        • 2 Find the direction vector of the line
        • 3 Write down the equation
      • Solution 2
        • 1 Find the normal vectors of two planes
        • 2 Find the cross product of two normal vectors which is the direction vector
        • 3 Find any point on the line
        • 4 Write down the equation
    • Find the equation of the plane perpendicular to the curve at the point
      • 1 Find the value of parameter t which is corresponding to the point
      • 2 Find the direction vector of the tangent line at the point
      • 3 Write down the equation
• 11.7 Curvature and Components of Acceleration
  • Curvature
  • Theoremn A
  • Exercises
    • Find the curvature for the given helix
      • 1 Write the position vector
      • 2 Find the curvature of the circle
    • Find the curvature and the radius of curvature of the curve traced by the position vector at the point
      • 1 Find the curvature by using the definition
      • 2 Find the variable value at the point
      • 3 Substituting the value
    • Find the curvature of the givenfunction x=f(t), y=g(t) at the point corresponding to the value of t and at the point
      • 1 Find the curvature by using the Theorem A
      • 2 Substituting the value of t
• 11.8 Surfaces in Three-Space
  • Cylinder
    • Generator is the moving line l
  • General Equation
    • F(x,y,z)=0
  • Quadric Surfaces Equation
  • Intersections of the surface with planes
    • Parallel to the coordinate planes
  • Types
    • Ellipoid
    • Elliptic Paraboloid
    • Hyperbolic Paraboloid
    • Hyperboloid of one sheet
    • Hyperboloid of two sheets
    • Elliptic Cone
  • Surface of Revolution
    • The equation of the surface generated by revoloving a curve F(y,z)=0 in the yz-plane about the y-axis is
  • Exercises
    • Find the equation of the surface generated by revoloving the equation on the coordinate plane about a axis
• 11.4 The Cross Product
  • Algebraic Definition
  • Theorem A
  • Theorem B
  • Theorem C
  • Area of parallelogram
  • Volume of parallelepiped
  • Exercises
    • Find all vectors perpendicular to two different vectors
      • 1 Find the cross product of two vectors
      • 2 Add a scalar which can be any real number
    • Find the equation of the plane through the three points
      • 1 Find two vectors
      • 2 Find the cross product of two vectors which is the normal vector of the plane
      • 3 Write down the equation of the plane based on a point and the normal vector
    • Find the equation of the plane through the point that is perpendicular to the two plane
      • 1 Find the normal vector of two plane
      • 2 Find the cross product of two normal vectors
      • 3 Write down the equation of the plane based on the point and cross product
    • Find the area of the triangle with three points
      • 1 Find two vectors
      • 2 Calculate the area of the parallelogram with two vectors as adjacent aides
      • 3 Half of the area in step 2 is the area of the triangle
    • Find the volume of the parallelepiped with edges
• 11.3 The Dot Product
  • Algebraic Definition
  • Theorem A Properties of the Dot Product
  • Theorem B
  • Theorem C Perpandicularity Criterion
    • • Orthogonal
  • Projection
    • Vector Projection
    • Scalar Projection
  • Equations of Plane in three-space
  • Distance Formula from a Point to Plane
    • The distance L from the point (x0,y0,z0) to the plane Ax+By+Cz=D is
  • Exercises
    • Find the angles between the vectors and determine which is orthogonal
      • 1 Find the dot product of two vectors
      • 2 If the dot product equals 0, the two vectors are orthogonal
    • Find the projection
    • Find the equation of plane through a point perpendicular to a vrctor
    • Find the angle between two planes
      • 1 Find two plane's normal vector
      • 2 Calculate cosα by using Theorem B
      • 3 Find the angle α (0<α<Π）
    • Find the distence between the parallel planes
      • 1 Find a point in the first plane
      • 2 Find the distance from the point to the second plane by using the Distance Formula
• 11.2 Vectors
  • Linear Operations (Theorem A)
  • Unit Vector
  • Decomposition of vectors
  • Exercises
    • Find the vector using given points
    • Express a vector in terms of other vectors
• 11.1 Caresian Coordinates in Three-Space
  • Octant
  • Distance Formula
    • The distance between P1(x1,y1,z1) and P2(x2,y2,z2) is
  • Mindpoint Formula
    • The midpoint of P1(x1,y1,z1) and P2(x2,y2,z2) is
  • Sphere
  • Plane
    • Ax+By+Cz+D=0
  • Parametric Equations
    • A curve in three-space is determined by the equations x=f(t), y=g(t), z=h(t)
  • Arc Length Formula
  • Exercises
    • Find the distance between two points
    • Find the center and radius of the sphere with equation
      • 1 Use the process of completing the square
      • 2 Write down the center and radius based on the standard equation
    • Find the length of the cycle of helix